智能车避障时的行为决策与路径规划算法

背景

根据智能车决策规划模型以及考虑周围实时环境变化带来的环境约束和自身条件约束，为车辆提供可行使域的过程就是路径规划，路径规划分为全局和局部规划两种。全局路径规划是在已知地图信息的条件之下，同时利用环境的局部信息和车辆实时反馈信息，从而生成可行驶区域以及车辆的参考行驶路径。但是对于全局路径规划而言未能考虑驾驶方向、道路曲率、速度以及环境中所出现的障碍物，同时智能车在真实环境下会出现不可预测的因素，因此必须考虑局部环境因素，故局部路径规划便应运而生。为了解决路径规划所带来的问题，现阶段已经有大量的方法被提出来。其中早期方法可分为三类：人工势场法、单元分解法、基于路网的方法。人工势场是通过模拟对目标的吸引与排斥从而产生一个阶梯状的势场，通过这个阶梯状的势场，按照阶梯势场的梯度找出最佳的可行驶路径。该方法被广泛应用于机器人的路径规划。单元分解法是将环境切割成凸的无障碍区域，这些凸区域被定义为单元。路网规划与单元分解类似都是将环境离散，然后进行图搜索，从而找到一条无碰撞路径。可视图法是路网规划的一种改进方法，它是将两个可见的点连接成一条直线，从而用搜索算法进行寻找可行路径。上述传统的路径规划方法大部分不会考虑智能车运动学或者动力学特性，规划的路径并不光滑，而且不考虑车辆的轨迹跟踪控制约束。基于多项式路径规划方法可以根据车辆初始状态与目标状态对需要变道的智能车进行变道过程中的路径规划，从而使得智能车在一定时间内可以到达指定车道。其中在随着多项式次数的增多，曲线拟合效果就越好，但是次数的增多会伴随着参数求解过程复杂，一般采用五次多项式进行车辆换道避障的规划。其中五次多项式公式为：

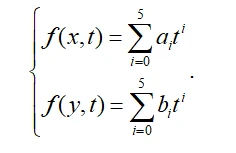
You F等基于五次多项式构造变道轨迹函数组，分别在横向和纵向建立多项式，通过增加纵向自由度的形式解决变道超车纵向车速变化的问题。Guoqing G等利用五次多项式记录不同工况下的换道路径数据，根据已有的数据利用遗传算法和BP神经网络进行训练从而得到最优驾驶员模型。基于多项式的路径规划在纵向和侧向都可以达到期望效果。但在纵向车速变化情况下自适应能力较差。B样条是另外一种比较特别的多项式拟合形式。它利用加权点生成中间状态来满足约束条件，在进行智能车辆路径规划过程中广泛应用。Guilin Z等在B三次样条的基础之上考虑了单轮模型并与电机动力限制相结合，将其应用在了单轮车上的路径规划。日本学者Maekawa T等在给定障碍物位置和工作区间几何条件的情况下利用B三次样条进行避障轨迹规划。贝塞尔曲线以其线条光滑且曲率小被广泛应用。康奈尔大学在2005年DARPA挑战赛上利用贝塞尔曲线生成符合车辆动力学的路径。Ma L等利用贝塞尔曲线完成了道路上的行为决策和在线轨迹规划。Bae I等对三阶和五阶贝塞尔曲线进行对比，得出满足起始曲率为0且舒适性最优的五阶贝塞尔曲线，并根据五阶贝塞尔曲线实时控制智能驾驶车辆的横纵向行驶轨迹。

智能车避障算法设计

——引言

车辆换道避障的行为决策需要满足行驶稳定和安全舒适的驾驶员意图，本文所设计的行为决策模型，主要结合车辆动力学，设计了一个动态风险评估模型保证车辆在换道避障过程中不会出现车辆失稳和碰撞的情况。本文基于非解耦五次多项式进行路径规划的设计，考虑安全性约束、边界约束和非完整性约束多个约束条件。利用QP算法将原本路径规划过程中非凸问题转换为凸优化问题并求解出最优路径。

——车辆行为决策规划

问题描述

在车辆的实际避障过程中，决策规划是自动驾驶最重要的部分之一。规划决策系统在处理完环境信息之后，基于车辆动力学的同时结合驾驶需求进行车辆行为的实时决策规划，主要分为行为决策和运动规划两部分，行为决策在满足交通规则、行驶安全等约束条件下生成驾驶意图；而运动规划主要是根据车辆状态和已知的环境信息，在考虑多重动态和多个约束条件下，确保车辆的安全性、舒适性和可靠性，实时获取车辆的期望轨迹。

坐标系转换

在Frenet坐标系下，非解耦五次多项式是弧长

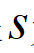
为自变量，横向偏移量

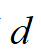
为因变量的空间函数。在进行路径规划过程中通常以路径连续性、平滑性、安全性作为主要的评价指标。如图1所示，在Frenet坐标系下建立切线向量和法线向量，将智能车的运动状态时刻分成

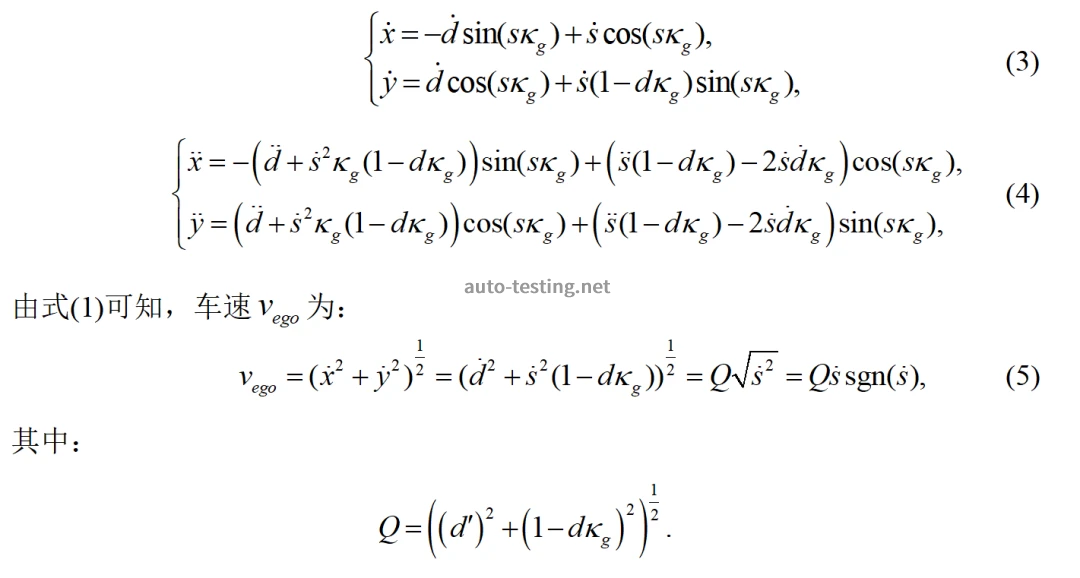
，使得车辆在拟合路径过程中，减少坐标信息的处理。

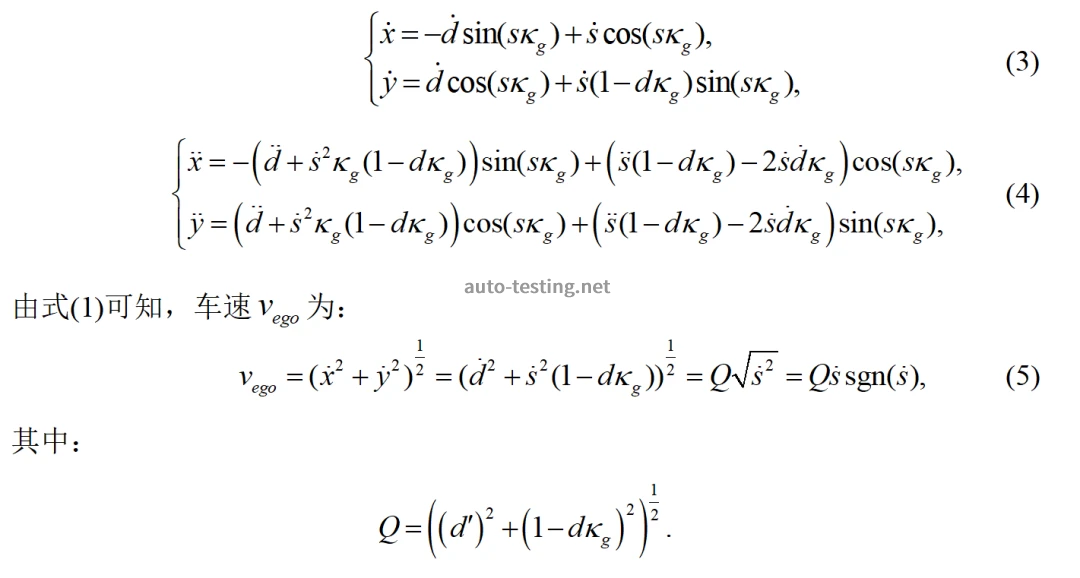
图1 Frenet坐标系

假设笛卡尔坐标系下车辆换道避障最优规划路径位置、曲率和航向角为：

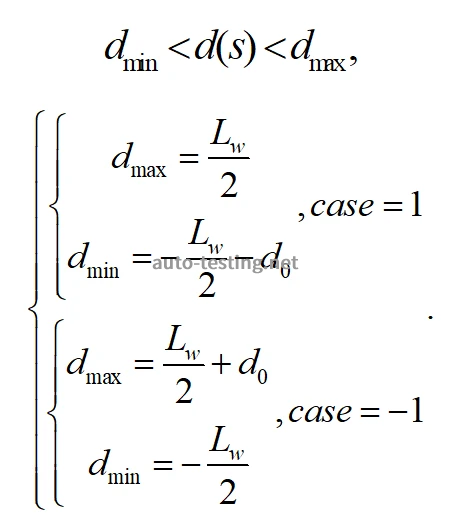
其中

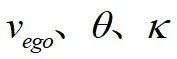
为规划路径上的速度、航向角、曲率。上式中所得的关系变量是以时间t为自变量，转换为曲线坐标系以弧长

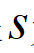
为自变量：

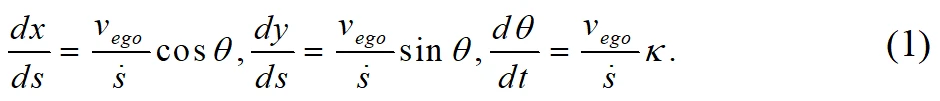
上式中

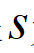
为车道中心线弧长并非局部路径长度。找出规划路径的曲率、速度、

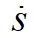
之间关系，即为简化推导过程，如图2所示，可得以下关系：

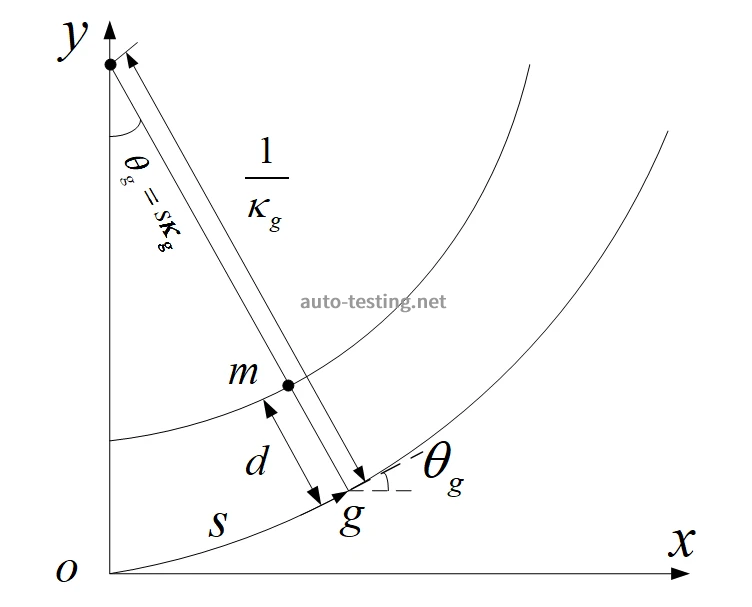
图2 笛卡尔坐标与曲线坐标系的关系

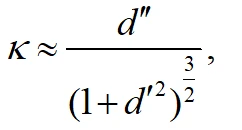
其中在上图中m点下笛卡尔坐标系的曲率，以时间t为参数，可得：

由上式(2)可知，为求m点在笛卡尔坐标系下曲率，需求m点在

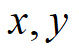
方向上的加速度和速度：

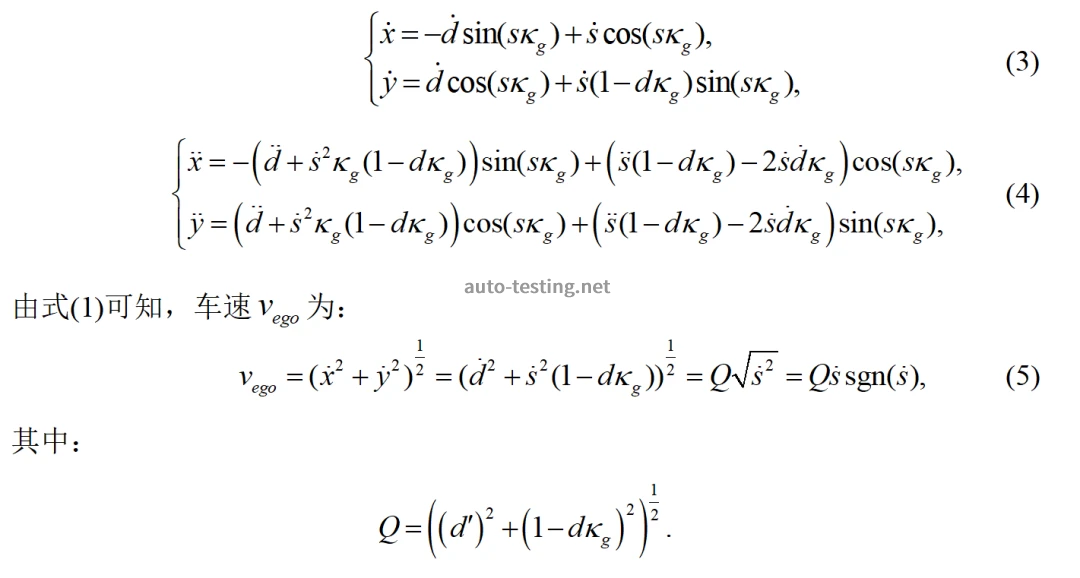
将(3)和(4)代入(2)得：

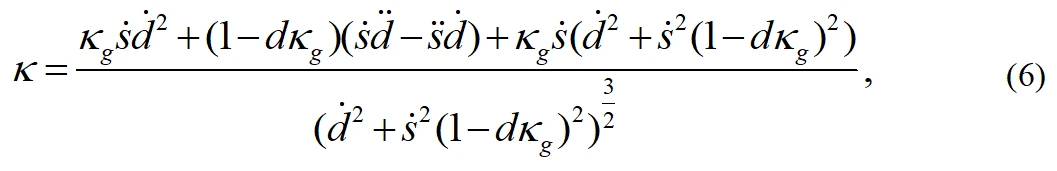
上式是局部路径关于时间t得一阶和二阶导，在Frenet坐标系下关于中心线弧长

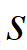
的函数关系为：

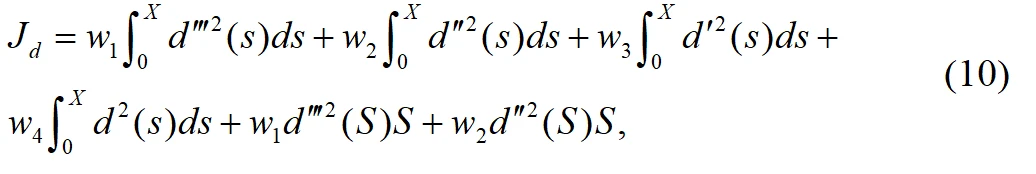
在实际弯道行驶过程中，局部路径的横向偏移量

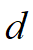
远小于车道中心线半径，故实际应用过程中，针对一个规划窗内的车辆动力学运动状态可忽略不计，即

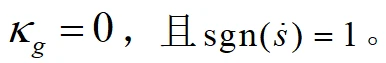
行为决策模型设计

为了设计更为安全舒适的路径，本章节的车辆行为决策以车辆在直道上换道避障为例(弯道情况与其类似)，在Frenet坐标系下进行行为决策规划。假设跟随车辆车宽为1.7m，设计的安全阈值为0.5m，即

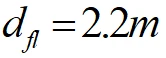
。车辆实际行驶的纵向距离

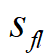
和行驶纵向车速

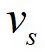
实时计算

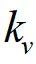
，当

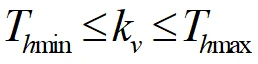
时，可进行换道避障，否则车辆存在碰撞或横向失稳风险。行为决策如下图3所示，详细的决策模型可参考公众号文章：优化思想及KKT原理在换道决策中的应用。

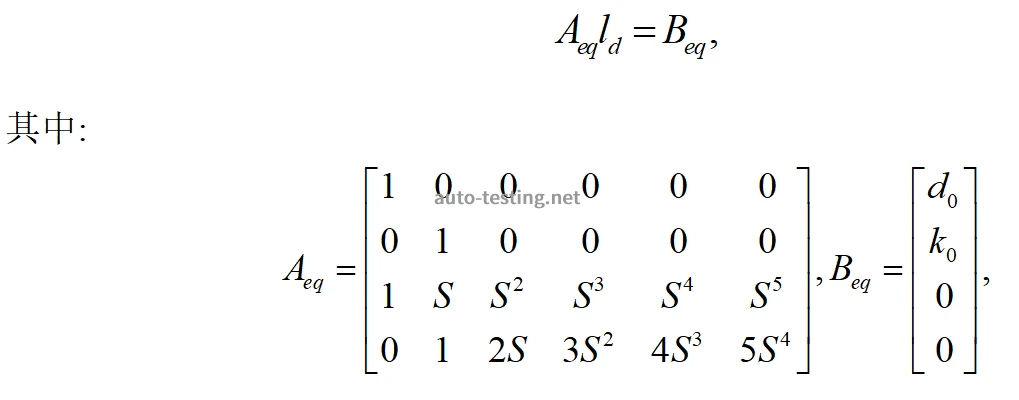
图3 决策规划动作图

——五次多项式路径规划

问题描述

根据行为决策结果，车辆将进行车道保持模式和换道避障模式的切换。其中两种模式在行驶过程中目标和参考线有所区别，本节主要以换道模式下的路径规划为例进行说明。

智能车动力学构型空间包含了时间维度、横向空间维度和纵向空间维度。在Frenet坐标系下既可以将车辆动力学问题优化成横向和纵向两个时空方向相互独立的问题，又可以将车辆动力学问题整合成单个横向时空优化问题，考虑换道过程中的路径的舒适性、安全性和平滑性等问题。

优化目标描述

(1)引导线选择

利用传感器可检测到车道线数据信息，其中相邻车道线目标车道

中心线方程信息：

目标车道中心线为：

其中

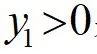
表示向左换道避障，

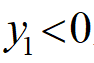
表示向右换道避障，式(8)为换道避障的目标车道线。

目标车道中心线作为参考线并不能直接用于车辆控制，需经优化处理成目标轨迹即引导线方可使用。如图4所示，在Frenet坐标系下，引导线为待优化的期望车辆行驶轨迹。在实际环境下，引导线需满足多重约束条件，并且平滑过渡到参考线上。

图4 规划引导线

(2)优化目标

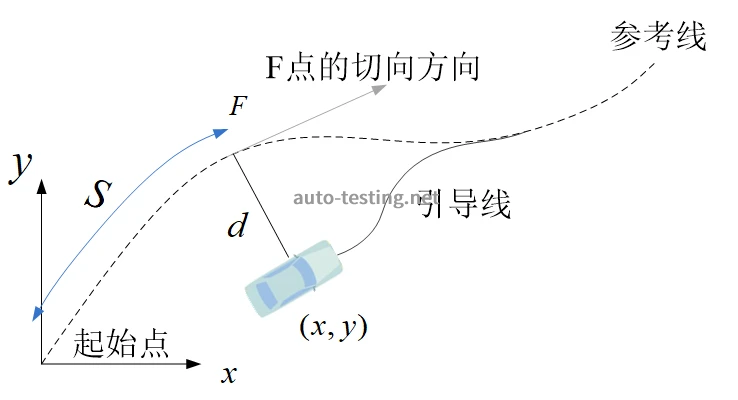
Frenet坐标系下，利用非解耦五次多项式描述目标行驶路径：

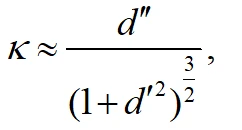
其中，

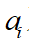
为待定多项式系数。

关于非解耦五次多项式路径规划优化目标主要是换道过程中的误差值、横向位移、航向角、道路曲率、道路曲率变化率以及换到完成后的状态误差组成：

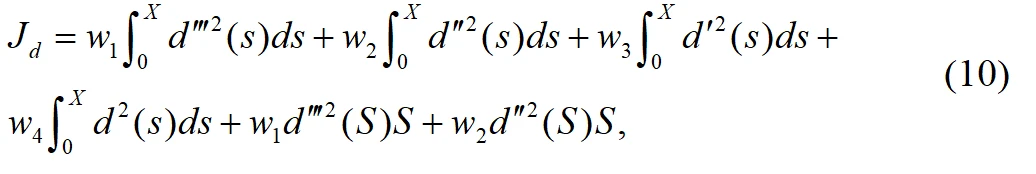
其中，

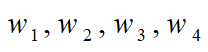
是目标优化过程中的权重系数，X其中是运动过程中的纵向距离窗宽度。

其中定义待优化变量

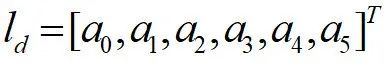
，优化目标可转换为：

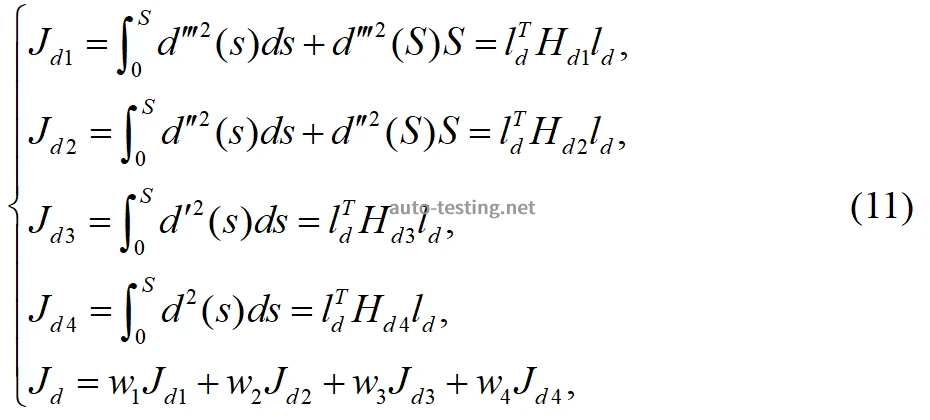
其中，

关于非解耦的五次多项式路径规划的优化目标可等价于：

其中，

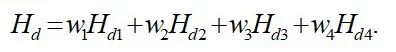
约束条件设置

其中约束主要包括外部、内部约束，内部约束是指车辆动力学或运动学限制从而带来的非完整约束，外部约束主要是外部环境、检测到的障碍物带来的约束。

1. 边界约束：假设车辆实际轨迹会一直沿着规划的路径向前运动，则对应的边界约束条件为

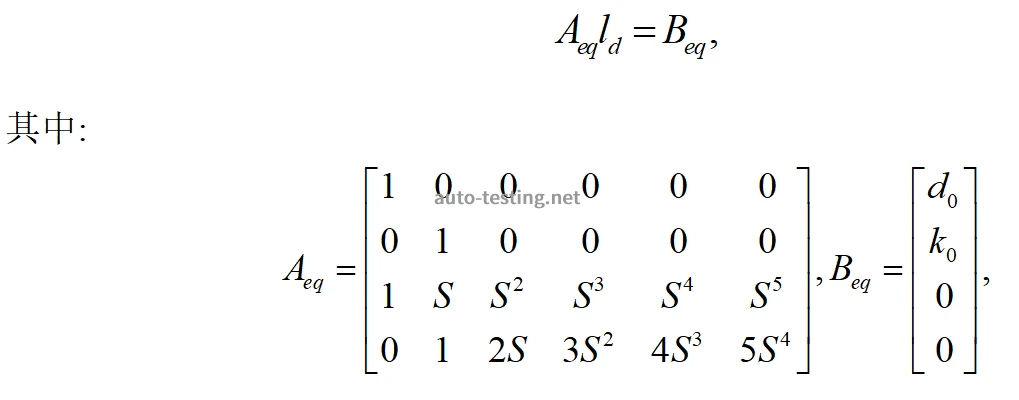
其中

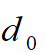
表示横向偏移量，

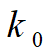
表示航向偏移量。根据边界约束条件，路径规划等式约束等价于:

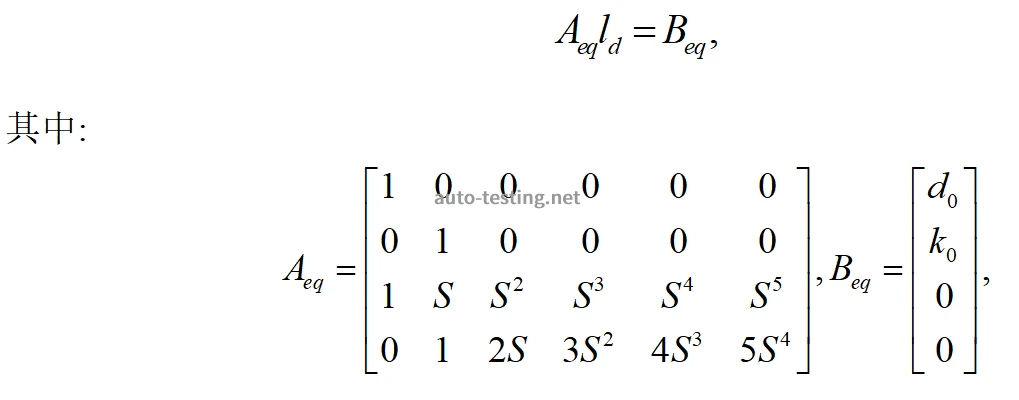
2.安全性约束：在车辆避障换道过程中，为确保换道的安全性，路径规划满足的约束条件为:

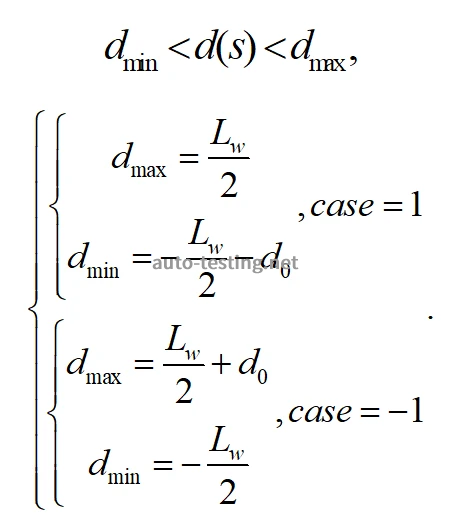
换道过程中以左为正，则以车辆向左换道为例，如图5所示。其中当

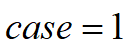
时，表示向右换道；当

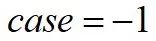
时，表示向左换道。

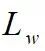
代表路面宽度。

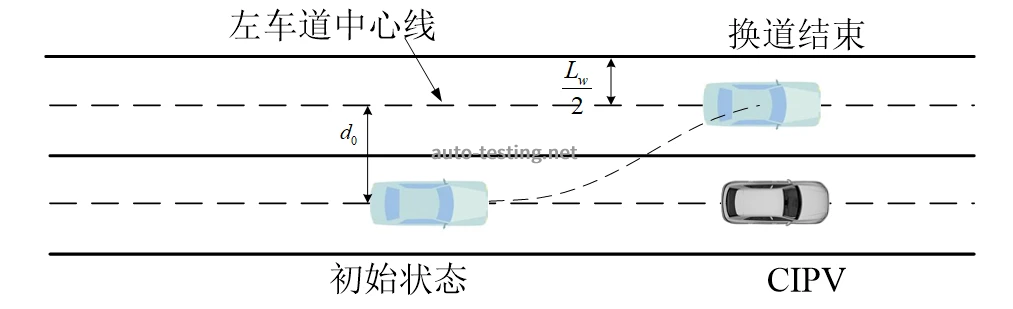
图5安全性约束示意图

非完整性约束：

对于车辆行驶轨迹的曲率约束最主要的是非完整约束。其中考虑到Fernet坐标系下曲率计算的非线性，则在一个规划窗内车辆动力学状态的变化较小可直接忽略，即曲率可表示为：

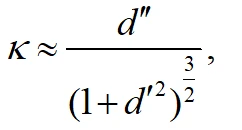
对于车辆Ackerman转向几何的曲率约束最重要的是非完整性约束:

其中，

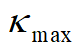
表示与车辆转向相关的最大曲率。即:

非完整性约束即曲率约束主要是针对汽车横向轨迹进行约束，即将非线性的非完整约束(13)转换成非线性约束条件(14)。

依据安全性约束和非完整性约束条件等价于:

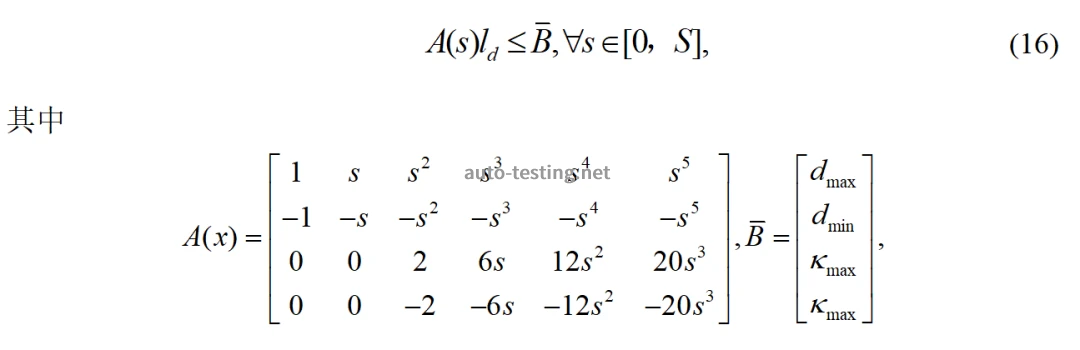
针对非解耦五次多项式路径规划的约束条件包含边界约束、安全性约束、非完整性约束即曲率约束。综上，在Frenet坐标系下，关于车辆非解耦的路径规划可以转换成求解标准的QP问题：

在标准QP模型(17)中，综合考虑非解耦五次多项式拟合目标路径的安全性约束、边界约束以及非完整性约束。因此，本节主要设计了换道过程中非解耦五次多项式路径规划模型，并成功转换为标准QP问题。

小结

在符合交通规则约束和行驶安全约束的条件下设计基于动力学的行为决策风险评估模型，利用非解耦五次多项式进行路径规划设计并将非解耦路径规划的非凸优化问题利用QP转化为标准的凸优化问题，从而求解出最优路径，最后利用已经确定好的LQR控制算法进行横向动力学控制，最终实现车辆的安全换道避障。