摘    要   

锂离子电池的温度监测对于先进的电池热管理系统（BTMS）来说至关重要，以提高性能并确保电池系统的操作安全性和可靠性。在真实的应用中，由于将传感器放置在核心内部的不切实际性，电池的核心温度是不可测量的，但又必须实时地在线估计。同时，在大功率应用中，由于电池表面与内部温度梯度较大，仅测量电池表面温度已不能满足先进BTMS的要求。当遇到传感器偏差和噪声时，电池芯温度估计将变得具有挑战性。为了提高电池核心温度估计的准确性和稳定性，采用基于Rauch-Tung-Striebel平滑技术和Unscented Kalman滤波的方法对电池核心温度进行重构，以应用于电池管理系统，平滑处理可以有效地进一步减小其估计误差。通过优化辨识出非线性热模型中的不可测参数。电-热耦合模型通过实验和CFD模拟进行了验证。仿真结果表明，不同电芯温度的平均误差小于1K。

01  前    言 

锂离子电池由于高能量密度、循环寿命和充电/放电效率而广泛应用于各种能源领域，例如电动车辆和能量存储场所。然而，电池系统的运行性能直接受到温度的影响，例如能量效率、循环寿命、安全性和可靠性。锂离子电池的推荐最佳工作温度范围为25°C至40°C 。当电池温度超过安全温度范围时，电池内部会发生副反应。一旦温度达到热失控临界点，电池的安全性将受到威胁。同时，在实际运行条件下，电池的表面温度和核心温度之间的温差甚至可能超过10°C。它使电池的核心温度提前达到热失控的临界点，从而发生热失控甚至爆炸。因此，核心温度的检测至关重要。通过将温度传感器放置在芯内的方法可以检测电池的电芯温度。但是，这增加了额外的制造挑战、成本和复杂性。而表面温度的测量并不能呈现细胞的全部温度信息。因此，有必要估计电池核心温度以确保电池安全并防止热失控。

一些研究应用电化学阻抗谱来估计电池的核心温度。虽然在实验室条件下可以准确估计核心温度，但将其在线应用于实际车辆具有挑战性。另一种方法是基于数据驱动的方法。Jiang, L.等人利用实际运行数据，通过精英保留遗传算法获得最优时间序列，并结合双向长短期记忆网络对电池的最高温度和最低温度进行预测。Jaliliantabar, F.通过应用人工神经网络来估计具有不同相变材料的电池温度。Mesgarpour, M.通过利用基于物理的神经网络和视觉跟踪方法来实时预测电池的温度分布。然而，数据驱动的方法对应用条件有着很高的要求。热物理模型的方法也得到了广泛的应用。Pang, H.等人基于电化学热耦合模型，考虑到热电偶的测量误差和噪声，仅使用输出端电压数据而不是温度传感器预测电池芯温度。其他研究通过基于降阶电热耦合模型的卡尔曼滤波方法估计电池芯温度。Sun, L.等人利用无迹卡尔曼滤波器（UKF）监测温度状态，考虑到辐射和观测的不确定性。虽然这些方法具有较高的估计精度，但由于对测量噪声的敏感性，在苛刻的外部条件下估计精度和稳定性是具有挑战性的。因此，本文提出了一种结合Rauch-Tung-Striebel（RTS）平滑技术和UKF的温度估计方法来重构电池模块的温度梯度。基于RTS的方法使用当前时刻和未来短时间内的温度信息以获得内部温度。本文的其余部分组织如下：在第二节中，开发了电池模块的多物理模型；第三节介绍参数识别；模型验证见第四节；第五节描述了基于RTS-UKF方法的热状态观测器；温度性能在第六节中讨论；第七部分是结论。

02  物理模型

在本节中，描述了电池模块模型、电池的电模型和热模型。同时，电池芯温度估计的过程呈现如下。图1示出了电池芯温度估计的过程。首先，通过测试不同荷电状态（SOC）和环境温度下的混合脉冲功率特性（HPPC），得到了内阻。在实验测试中，通过测量不同SOC周期内不同温度下的电压变化，计算出开路电压的温度系数。电池的发热量由电气模型计算。然后，模型参数识别的遗传算法（GA）优化方法的基础上的计算流体动力学（CFD）模拟数据的电池组。最后，核心温度估计的RTS-UKF方法的基础上的电池的表面温度。

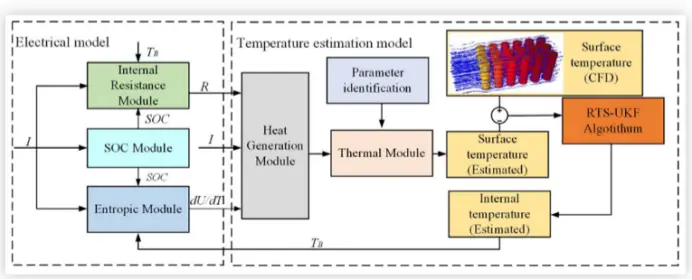
图1 核心温度估计的框架图

电池模块型号

图2显示了基于空气冷却模式的电池模块模型。该模型由m行和n列单电池组成。由于可靠性高，成本低，采用风冷方式。由于对称排列，因此选择虚线框中的一排电池作为研究对象来估计电池组中的核心温度。电池之间的间隔在水平和垂直方向上都是LD。

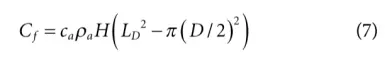
图2 风冷电池模块模型

热模型

电池的热动力学建模的基础上的经典的传热问题。根据能量守恒定律，将两态电池组热分布模型定义为：

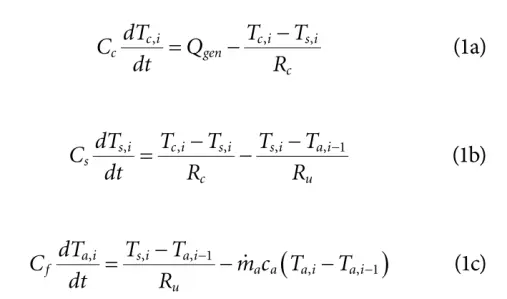
其中核心温度Tc和表面温度Ts是两种状态。i表示电池模块中的第i个电池。Ta是电池周围的空气温度。Qgen是电池的发热量。Cs和Cc分别表示表面和芯集总热容。Cf是电池和空气之间的等效热容量。Rc表示芯和表面之间的热阻。Ru是表面和空气之间的热阻。Ma和Ca是空气的质量流量和比热容。

电模型

电池的发热发生在充电和放电过程中。根据Bernardi的描述，热生成是焦耳热（不可逆）和熵热（可逆）的总和，并表示为：

其中Qirr是由于内部电阻引起的焦耳（不可逆）加热，并且由下式表示：

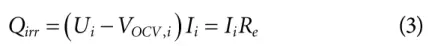
其中，Ui和VOCV是第i个电池的端电压和开路电压。Re是内部电阻。Qrev是可逆熵损失，由下式给出：

其中Ti是电池温度，它的值是核心温度和表面温度的平均值。dVocv/dT是熵系数。在不同环境温度和SOC下，通过实验测试获得了电阻和熵系数，具体过程见下文。

03  系统参数辨识  

电池电阻测试

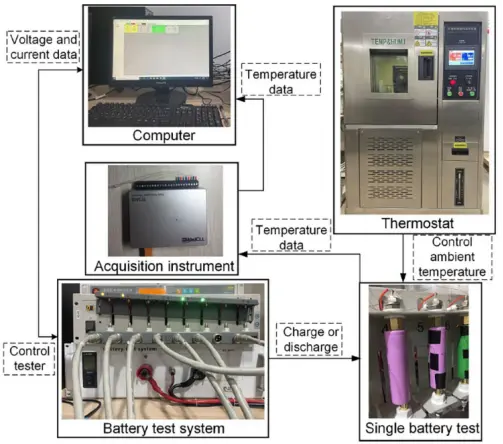
内阻由欧姆电阻和极化电阻组成，这些值通过HPPC测试计算。根据有关文献，发现欧姆电阻和极化电阻两者与SOC和电池温度有关。为了提高内阻模型的准确性，HPPC实验在不同的环境温度下进行了测试。操作温度设定为298.15K至318.15K，放电速率为0.5C至2C。所有HPPC实验涵盖0.1至1的SOC。图3展示了实验设备。

图3 实验设备示意图

根据HPPC的实验数据，应用多项式响应面模型（PRSM）建立了不同SOC和温度下的HPPC内阻。PRSM给出如下：

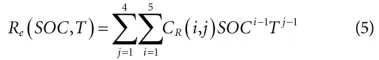
其中CR如下给出：

熵系数检验

熵系数与SOC有关。因此，在实验测试中通过在不同SOC周期期间在不同温度下的电压变化来获得该值。应用PRSM对实验数据进行拟合，熵系数模型由下式给出：

其中系数Ccoeff如下给出：

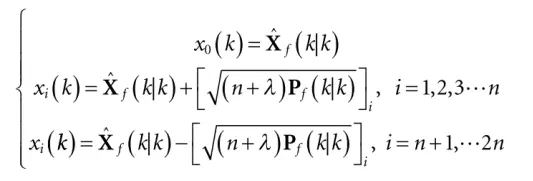
参数辨识

参数辨识的方法有很多种，如广泛使用的递推最小二乘法。但该方法精度较差，无法满足模型的要求。因此，基于遗传算法的优化算法应用于参数识别。根据等效热容的描述，按下式计算：

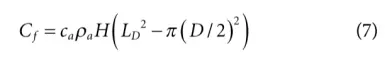
其中ρa是空气的密度。H和D是电池的高度和直径。LD是电池单元之间的间距。模型参数和确定的参数列于表1中。

表1 本研究中的参数

   04  验    证   

CFD模拟验证

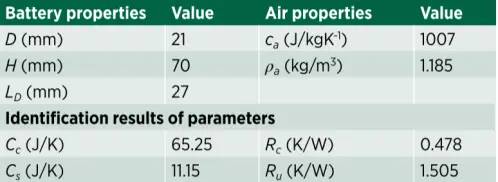
在本研究中，使用4.8Ah NMC 21700圆柱形锂离子电池。为了验证发热模型，通过Lanb电池测试系统（BT-2018）在不同放电速率（0.5C、1C、1.5C、2C）下对电池单元进行测试。测试电池放置在恒温器中以保持所需的环境温度。图4表明模拟数据与实验数据一致。

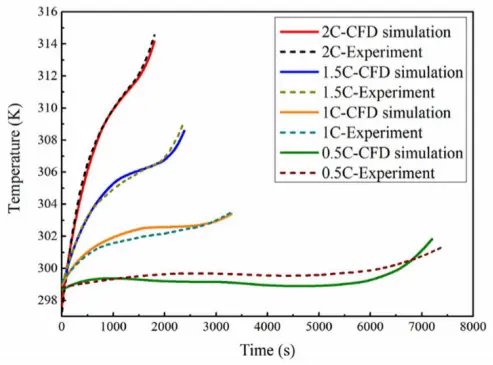
图4 单电池在不同放电率下的实验和模拟

电池模块热模型的验证

在本节中，DST循环用于电池模块热模型的确认。通过比较电池的热模型数据和CFD模拟数据，验证了电池的热模型。由于电池的内部核心温度在实际应用中是不可测量的，因此表面温度的准确性代表热模型的准确性。初始环境温度（Ta，0）和电池温度（Tc，0，Ts，0）被设置为298.15K。

图5显示了电池1和电池6的表面温度。可以看出，模型的温度接近CFD模拟的温度。误差性能如图6所示。与电池1的误差相比，电池6的误差由于环境温度计算中的计算误差而具有更高的误差。由于流体计算的复杂性和困难性，在计算电池周围环境温度时会出现一定的误差。然而，平均误差小于1K，显示了热模型的高精度。

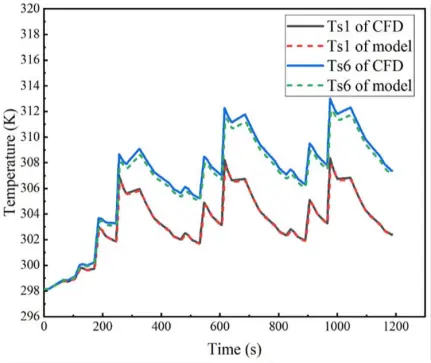
图5 电池1和电池6的表面温度

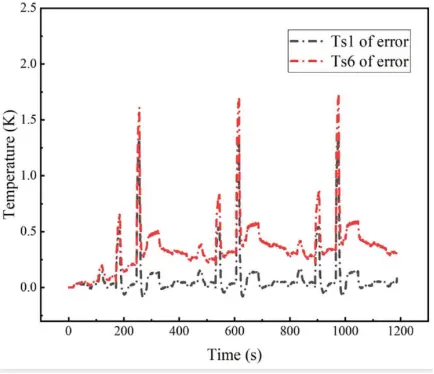
图6 电池1和电池6的模型误差

05  热状态观察器

对于实际应用，电池内部的核心温度难以测量。如果将热传感器设置在电池内部，将引起不可逆的变化。有效的方法是基于电池的表面温度来估计核心温度。本节详细介绍RTS-UKF方法来估计核心温度。

RTS-UKF方法

根据有关文献，RTS-UKF的核心思想是利用固定区间内的所有测量信息，在区间内的所有时刻获得最优估计。该方法由前向滤波和后向递归两部分组成，其原理图如图7所示。前向滤波由UKF（对于i=k，k+1，......，k+n）进行，以获得状态估计和误差协方差的先验估计、后验估计和互协方差矩阵。状态估计和误差协方差存储在前向滤波过程中。这些存储的值将被用作后向递归中的输入，并且将在后向平滑过程期间通过状态向量的后验估计获得最优结果（对于i=k+n，k+n-1，......，k）。

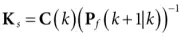
图7  RTS-UKF方法的示意图

RTS-UKF算法的具体步骤如下：

Step 1:在时间步长k处生成sigma点和权重因子

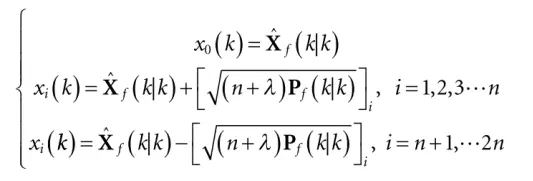
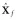是状态向量，Pf是误差协方差。

Step 2:通过动态模型更新sigma点

Step 3：计算预测均值

     计算预测协方差Pf

      计算互协方差C

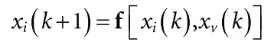
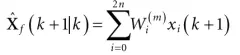
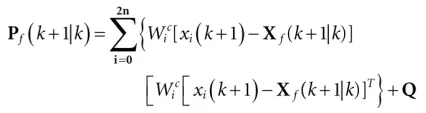
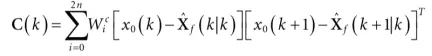
Step 4：计算平滑器增益Ks

       计算平滑均值Xs

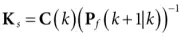
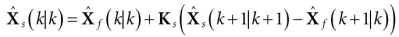
                计算协方差Ps

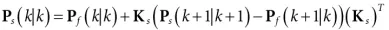
 06  结果和讨论  

在本节中，讨论电池1和电池6的内部温度估计。同时，对估计的误差进行了分析。最后，将RTS-UKF方法与仅使用UKF的方法进行了比较。计算流体力学模型排列成一条直线，如图2所示。对CFD模型中的固体和流体区域进行网格划分，并进行网格独立性检验。在DST放电条件下计算电池模块中的电池单元的相同热生成。空气的入口温度设定为298 K，空气的入口速度为0.5m/s。由于雷诺数小于2300，因此在CFD模拟中选择层流。液体区设置质量流量入口和压力出口。通过CFD模拟得到了各电池的表面温度和核心温度。

内部电池温度估计

本节使用DST循环。初始温度设定为298.15K。基于CFD模拟数据，核心温度作为真实的值获得。为了验证核心温度估计的准确性，电池1和电池6的核心温度及其估计误差在图8和图9中示出。图8显示了在DST循环下电池温度快速上升。比较电池1和电池6，核心温度随着流体流动的方向显著增加，特别是在多个循环之后。

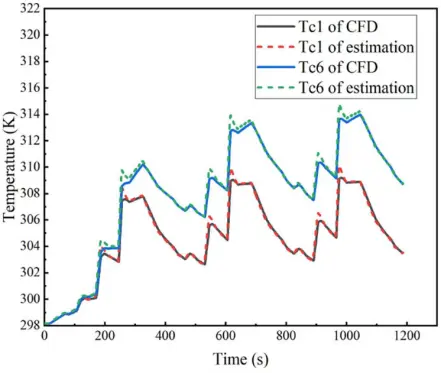
图8 电池1和电池6的电池芯温度

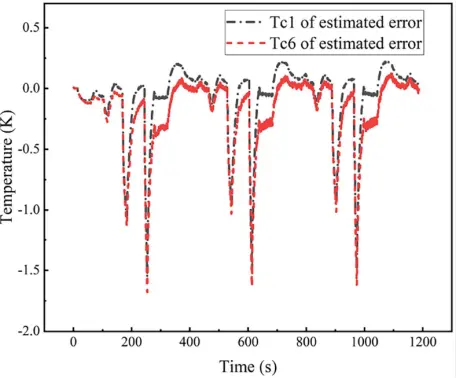
图9 电池1和电池6的电池芯温度估计误差

电池1或电池6的核心温度估计接近CFD模拟数据。与表面温度的情况类似，电池6的核心温度估计的误差高于电池1的核心温度估计的误差。然而，平均误差小于1K。估计结果表明，在核心温度估计的良好性能。该方法能够准确估计电池模块的核心温度。同时，通过比较核心温度和临界点温度，可以有效地防止热失控。

RTS-UKF与UKF的比较

在本节中，与RTS-UKF方法相比，UKF被实施用于核心温度估计。图10和图11描述了通过这些方法的温度估计及其误差。虽然RTS和UKF方法都具有低估计误差，但是RTS方法具有更高的估计精度，特别是对于电池6。对于时间步长k处的估计，RTS方法使用跨时间间隔的测量和估计数据，而UKF仅使用时间步长k-1处的测量和估计数据。通过增加平滑间隔时间来提高温度估计的精度。

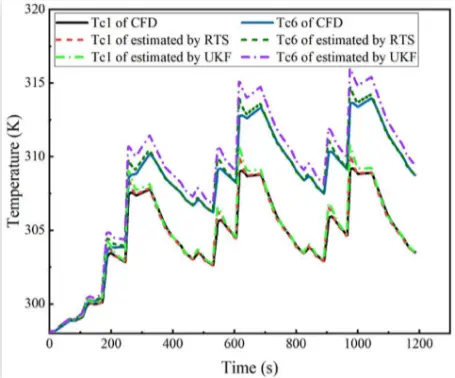
图10  RTS-UKF和UKF方法之间的比较

图11  RTS-UKF和UKF方法之间的估计误差

07  结    论 

电池芯温度估计对于电池系统的安全性和可靠性至关重要。在本文中，模块化和可扩展的电池热模型建立的核心温度估计。首先，在HPPC测试的基础上，选择PRSM来描述作为温度和SOC的函数的内阻和熵系数。其次，利用遗传算法对电池热模型的未知参数进行辨识。通过CFD仿真对电池热模型进行了验证，平均误差小于1K。最后，电池的核心温度估计应用RTS-UKF方法。结果表明，RTS-UKF方法具有较高的估计精度，估计误差小于1K。对UKF和RTS-UKF两种方法进行了比较。结果表明，RTS-UKF方法的附加平滑比UKF方法具有更低的估计误差，特别是对于电池6。此外，所获得的结果表明，在电池1和电池6之间观察到6K的最大温度均匀性。同时，还监测电池的核心和表面温度之间的温度差，以避免热失控。该研究可为热管理系统的温度控制提供参考，有效提高安全性和可靠性。

文献来源:

Zhu, W., Li, B., and Zhong, H., “Lithium-Ion Battery Module Internal Temperature Estimation based on Rauch-Tung-Striebel Smoothing Technique,” SAE Technical Paper 2023-01-0770, 2023, doi:10.4271/2023-01-0770.