寻找供应商
广告
首页 > 汽车测试技术 > 正文

基于仿真的自动驾驶可靠性估计（二）

2023-10-27 09:13:04·  来源：赛目科技  
　

前 言 

基于仿真的自动驾驶可靠性估计（一）中已经介绍，使用定步长泛化、朴素蒙特卡罗等方法生成验证自动驾驶系统的仿真场景难以在可以接受的成本内精确估计被测试系统在指定逻辑场景即测试空间内的失效概率。本文将由此出发，介绍若干可以用来估计罕见事件发生概率的可靠性分析方法。


01. 问题定义


我们将一个拥有D个可泛化参数的逻辑场景等价于  维参数空间  ，其中  是一组随机变量，其分布函数由逻辑场景决定，而  的一组具体取值  即为此逻辑场景下的一个具体场景。

被测试自动驾驶系统或车辆在某一具体场景  中失效，指该系统及车辆的某项评价指标（kpi）处于失效域中。我们用  表示某项kpi在场景  上的取值，不失一般性地用  表示此项kpi处于失效域中。故被测试系统或车辆在某一逻辑场景中的失效概率等价于对应测试空间中，参数组合落入失效域的概率，即


其中为此逻辑场景中参数的联合分布。

本文剩余部分将介绍若干精确高效估计此概率的可靠性分析方法并通过数值实现说明其效率。一般我们会在标准正态空间中使用这些可靠性分析方法，故我们提前使用Rosenblatt变换将测试空间转化为标准正态分布空间，之后的讨论均基于标准正态分布空间。


02.一阶可靠性分析方法（FORM）


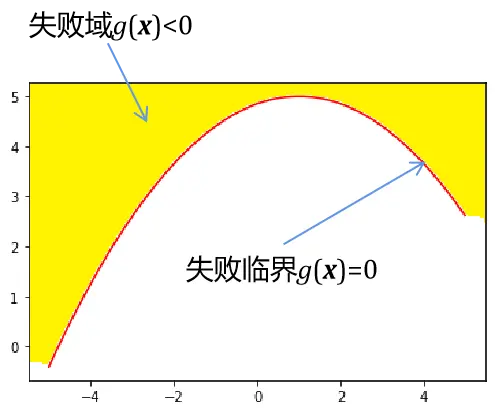
一种经典的可靠性分析算法是将  在失效临界面（即  的区域）上的一个点  利用泰勒展开进行线性近似，即  再通过  来估计  。如下图所示，右上角的区域为失效域，FORM用线性展开即黄色线以上的区域来代替实际失效区域。

图片

显然失效临界的形状及  的选取对近似的结果有很大的影响，直观想来我们会选取失效临界中最可能的点（实际是似然函数最大的点）MPP做为展开的中心  ，即      此时利用正态分布的性质及  的约束可以证明  其中  为标准正态分布函数的概率分布函数，  为原点到MPP的距离。可以看出FORM的精度取决于失效临界与线性边界的差距，而FORM算法的效率只取决于寻找MPP算法的速度。最早使用Rackwith-Fiessler算法来快速寻找MPP点，然而此算法并不能保证收敛，故在Rackwith-Fiessler算法不收敛时可以使用更为复杂的优化算法来实现，例如NLPQL。


03. 方向采样算法


将测试空间考虑成一个多维球体，若在每个方向上存在最多一个失效临界时，可以通过方向采样算法估计失效概率  。其基本原理是

1. 在半径为  的层球面进行均匀采样，并记录其中的失效场景；

2. 对失效场景所在的方向插值求解此方向的失效临界场景；

3. 注意测试空间为  维标准正态分布空间，故其中任意一点与原点距离的平方服从自由度为的卡方分布（  ），故可对失效概率估计如下


其中  是总采样数，  是失效方向数，  是第  个失效方向的临界场景与原点间的距离。

图片

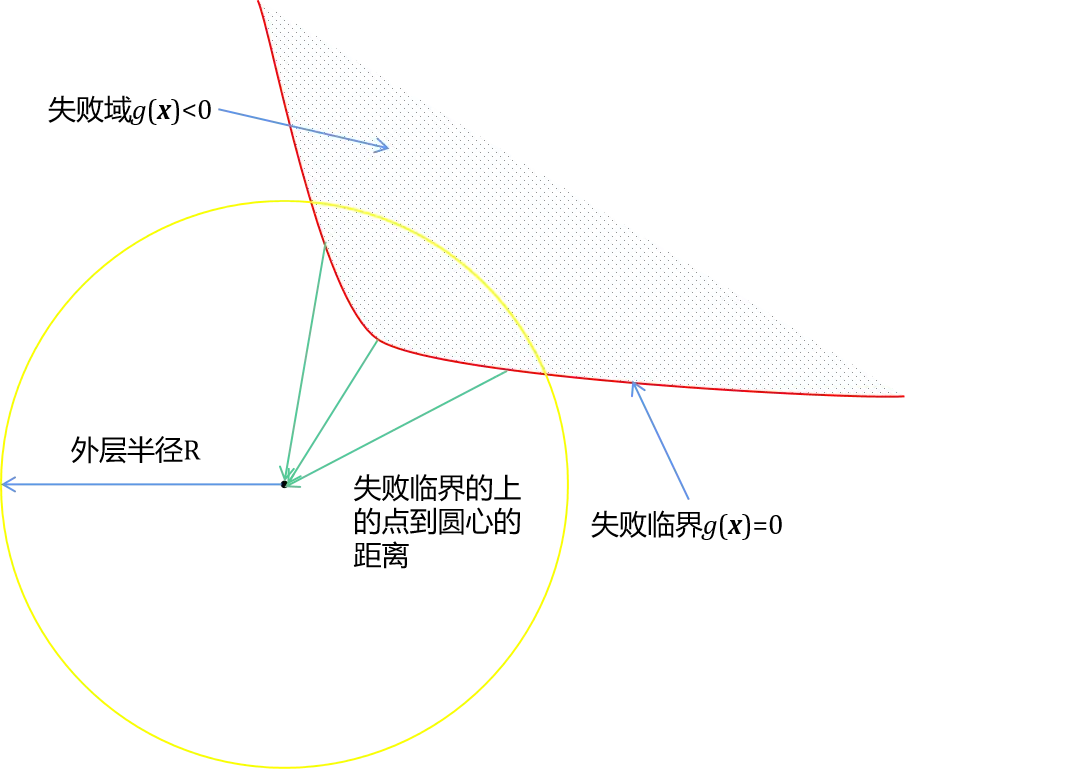
通过上面的介绍可以看出，方向采样算法无法观察到距离原点超过R的失效场景。在标准正态分布空间中无法观测的失效场景概率占比小于等于  ，故往往  取比较大的值例如  至  ，如此漏掉的失效场景占比仅在  至  ，是完全可以接受的。影响此算法精度的另一个因素是在外层球面采样的均匀程度，我们使用球面拉丁超立方采样代替传统的方法获取高维球面上的超均匀样本，用相同数量的样本实现对球面更好的覆盖。

图片

三维球面的均匀采样，左侧为传统方法，右侧为球面拉丁超立方采样，红色为寻找到的危险场景


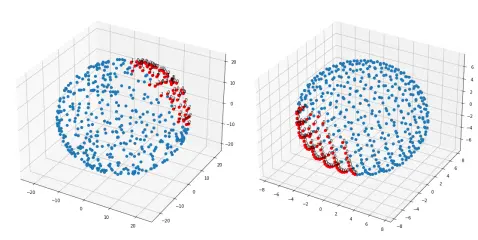
04. 重要性采样算法


重要性采样算法直接从蒙特卡罗方法失效的原因出发，使用提议分布  来代替真实分布  以期采集到更多的失效场景，并根据下面的方法估计失效概率  其中  是根据提议分布  的采样数，  是其中的第  个样本观察值。可以简单的看出重要性采样算法是失效概率的无偏估计，但算法的精度（相对误差）主要取决于提议分布的选取，在最优提议分布，  ，下  的相对误差是0！但是这样的提议分布显然是无法获取的，因为分母  本身就是我们要估计的量，所以实际应用中会采用各种方法来逼近  。我们选取混合高斯分布作为提议分布，使用交叉熵优化的方法基于每轮采样的结果自适应调整提议分布中的参数，实现对全部主导失效域的覆盖及失效概率的估计。下面的图说明了使用重要性采样的方法，自适应调整提议分布寻找失效样本和失效临界场景的过程。图片

重要性采样算法。其中蓝色点为安全场景，黄色点为本轮采样中较危险场景，红色点为失效场景，紫色点为失效临界场景。其中左上和右小角的是小边界为线性，左下和右上角的失效边界为非线性。


05. 数值实验


下面将用2个数值实验，证明不同可靠性分析算法的有效性。

数值实验一：

可靠性分析方法 FORM
测试空间
kpi函数
理论失败概率

图片

由于kpi函数的连续性及凸凹性较好，使用Rackwith-Fiessler算法快速迭代寻找MPP，得到如下实验结果

失败概率估计
相对偏差 16%
相对误差 0，FORM方法不使用随机采样
kpi函数调用次数 5次，5次迭代寻找MPP

图片

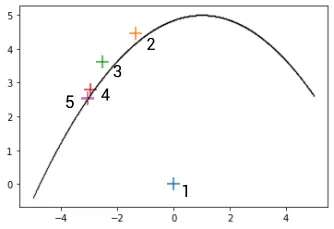
可以看当线性展开可以比较好的逼近失效临界是，FORM方法可以很好的估计失效概率。此例中虽然无法在全局使用线性展开逼近失效临界，但在MPP点附近逼近效果较好，即在对失效概率贡献最大的区域逼近效果较好，故可以得到较好的估计效果。

数值实验二

实验二中我们使用  测试空间中的Katsuki函数作为kpi函数，即          Katsuki函数通过是具备了不同形状的失效临界，其理论失效概率为  。使用方向采样及重要性采样对其进行估计，下面将展示两种算法的结果

图片

图片

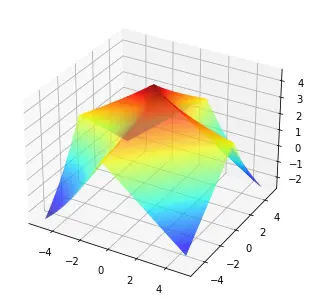
此实验中方向采样算法的球面采样数为100，临界面寻找的最大迭代次数为10；重要性采样每轮采样数为500。因为测试空间维度较低，方向采样有着非常优秀的表现，同时两者对比蒙特卡罗方法都体现出了超高的效率。需要注意的是，虽然重要性采样使用的kpi函数平均次数更多，但在并行仿真下实际只有4轮仿真；而kpi调用次数较少的方向采样因为缺乏并行仿真支撑能力，耗时反而更长。

最后对不同的可靠性分析算法能够适应的情景做出分析，需要注意的是蒙特卡罗方法或拉丁超立方/sobol方法虽然不受测试空间的限制，但其效率仅能应对概率在  及更大的情况。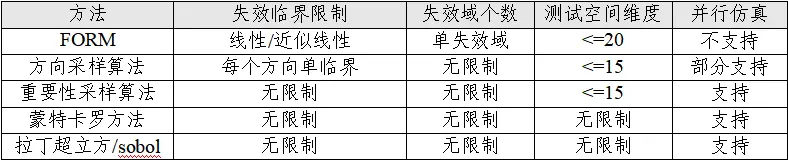图片


分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• 新型BREZZA和FRONX的空气动力学发展 • 一文讲清中、欧、美对智能远光控制IHBC的法规要求
• 理工雷科：电磁环境建模技术在智能网联汽车仿真测试中的应 • 测试基础｜汽车软件测试术语解释
• 带载温度循环耐久（PTCE）的深度解读 • 400公里/时，超级跑车选用imc验证车辆行驶安全
• 关于汽车电子电磁兼容系列标准大盘点 • 一些关于实现整车级SOA软件架构的建议
• 近距离横向行驶道路车辆的气动阻力 • 一文讲清欧美日澳对倒车影像的法规要求
0 条相关评论
  • 广告
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026917号-25