电动汽车电池包随机振动疲劳及优化分析

摘 要：电池包作为电动汽车重要的组成部件，路面传递的随机激励是电池包失效的重要原因。本文根据有限元建模，单位载荷的应力响应求解及疲劳损伤的计算。对电池包存在疲劳损伤值过大的情况，研究了通过提升电电池包模态频率以改善随机振动疲劳特性的优化思路。最后再通过进行台架实验，验证了所分析思路和优化效果的有效性。

关键词：电池包　随机振动　疲劳　功率谱密度

近年来，汽车行业面临巨大变革，产业生产模式、竞争格局都在发生深刻变化，全球电动汽车销量再创新高，电动汽车将成为制造业核心竞争力提升中的重要一项。由此可见，在市场及政策引导下电动车将替代燃油车成为主要的交通运输工具，其相关技术的开发也成为车企重点摸索的方向。

电池包系统作为不可缺少的核心部件，是车辆运行提供动力的心脏，其结构安全至关重要。在车辆行驶过程过程中，受路面传递而来的外部振动载荷复杂，且随机性大。因此，研究电池包在随机外部振动载荷下的结构特性，具有重要的工程意义[1]。戴江梁等[2]基于随机振动理论与频域疲劳分析法，研究了电池包结构的失效机理。王文伟等[3]基于三区间法计算了测试标准下电池包结构的振动疲劳特性。孙小卯等[4]基于电池包动态特性，研究了电池包在振动过程中产生的疲劳问题。本文将主要从电池包结构的随机振动疲劳方面进行分析研究。

1　电池包模型建立

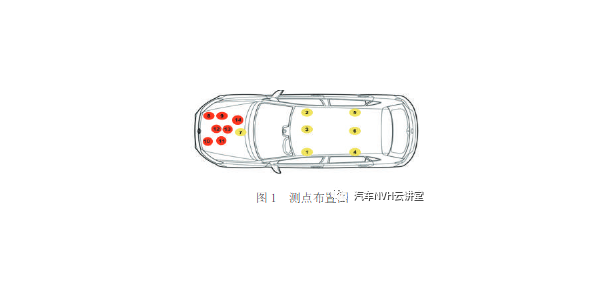
本文研究的电池包结构主要包括了电池包箱盖，电池模组，箱体及电池包底板等，为提升计算效率，建模之前，将电池包中包含的线缆、接口、继电器等对电池包结构性能影响不大模块省略。本文采用Hypermesh软件进行建模，建模过程中将尺寸较小的结构如圆角、翻边进行适当简化[5]。电池包整个箱体材料为AL6061，电池包箱盖和底板材料为Al5083，电池包整体重量545kg。电池包本体结构通过抽中面及壳单元对电池包进行网格划分，单元平均尺寸取8mm。对箱体结构中一体成型的部分，在公共边处采用共节点的方式连接，对焊接形式的连接结构，采用焊缝单元（Hexa+Reb3）进行连接。电池模组采用六面体单元进行网格建模。对于安装孔，根据螺栓选型的尺寸添加washer，并采用全约束的Reb2单元抓取washer上的单元节点。通过bar单元模拟螺栓连接。检查网格单元质量，不能存在重叠或无连接的孤立单元等。基于上述建模规范及标准，建立好的电池包网格模型如图1所示。。模型共有单元数1002423个，包含节点数896291个，其中三角形单元占比为0.2%。

2　电池包随机振动疲劳分析

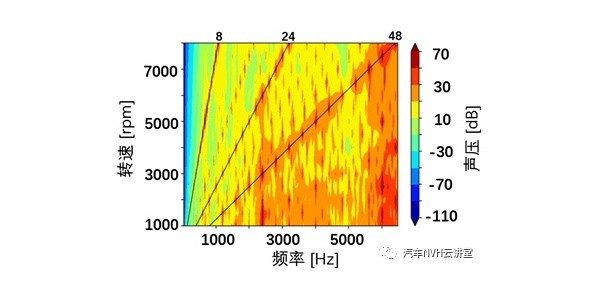
基于随机振动疲劳的理论分析，首先需获得在频域内，单位载荷下电池包结构的应力响应。本文采用Nastran求解器，约束电池包26个安装点（箱体22个，箱盖4个）的全自由度。根据国标GB/T31467.3-2015要求，求解频率范围为0~200Hz，并分别从X、Y、Z三个方向加载单位加速度（1G）激励，进行模态频率响应分析，最终获得电池包的三方向载荷- 应力响应的传递函数曲线，如图2所示。

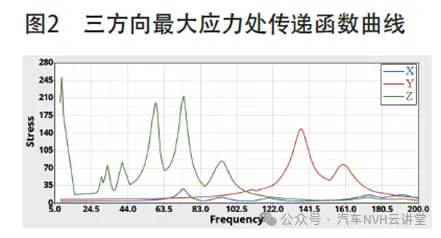
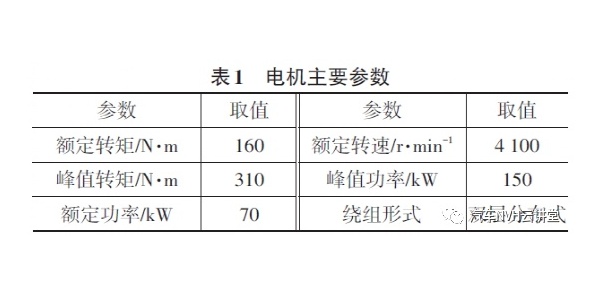
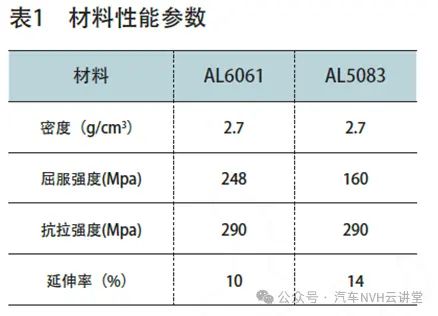
由计算结果可知单位载荷在电池包Z向产生的应力较大，与其他两方向相比，Z向工况较为恶劣。在得到传递函数的基础上，对电池包随机振动疲劳的求解，还需要通过材料性能近似推算材料的SN曲线。电池包材料参数如表1所示。

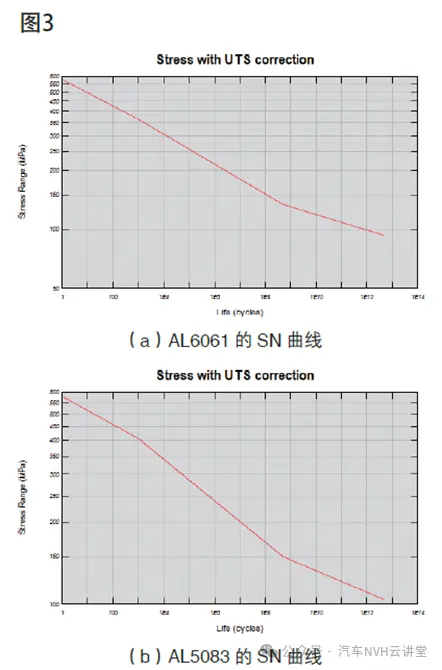
通过材料参数近似拟合的SN曲线如图3所示。

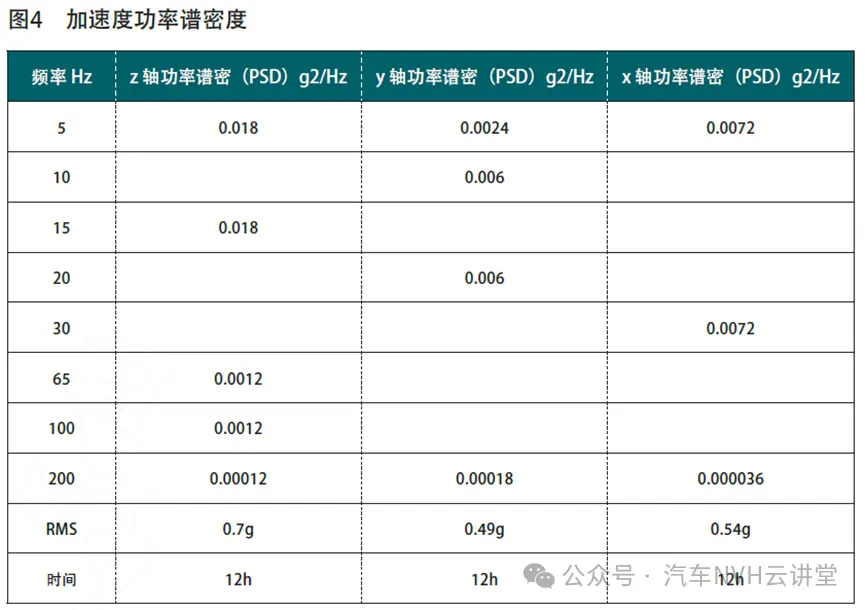
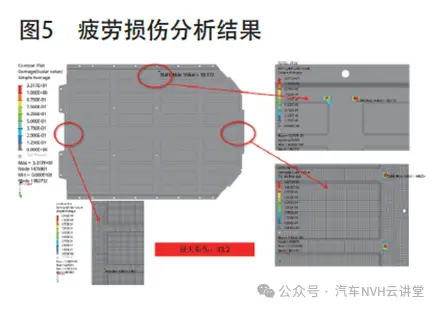
本文参照企业实验标准的加速度激励功率谱密度，如图4所示，并基于Dirlik法及goodman平均应力修正法，在Ncode软件Vibration模块中对电池包疲劳损伤进行求解计算。计算结果如图5所示。从分析结果中可知。电池包损伤值为33，远超过损伤值小于1的要求，最大位置位于底板的前、后、中部的固定孔处，并呈现对称式分布。通过图4发现，Z向功率谱密度在频率5～15Hz区间内最大，正好与传递函数中Z向的最大应力响应相重合，两者叠加可造成应力功率谱密度在5～15Hz频率区间内峰值变大，最终造成电池包结构的损伤出现失效风险。因此，对于电池包振动疲劳性能的优化主要从避免传递函数的最大应力响应频域区间与激励载荷的峰值频域区间重合。

3　电池包疲劳性能优化

为使得传递函数的频域响应区间避开5～15Hz范围，可通过提升电池包结构的刚度，以增加电池包在低频区间内的局部模态。由于电池包底板的损伤值较大，重点提升底板的局部刚度。为此，在底板与箱体部分可接触范围内增加玻璃胶粘接。采用同样的分析方法，求解电池包单位载荷应力响应的传递函数，如图6所示，并计算电池包的疲劳损伤，如图7所示。

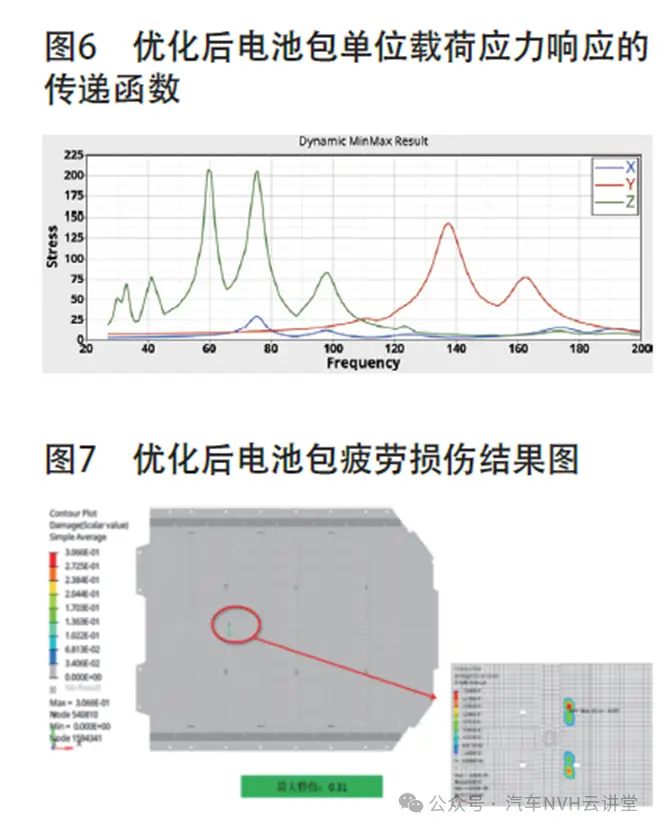
由图5、图6结果可以看出，在20～50Hz内单位载荷的在三方向的应力响应都比较低，Z项的响应峰值出现在60Hz左右处。而最大损伤位置也不在底板处，而是发生在箱体内部，并且最大损伤值只有0.3，满足设计要求。由此可见，本文提出的优化方法有显著效果。

4　实验验证

根据优化方案的结论，制作电池包样件。按图4中加速度激励功率谱密度作为台架随机振动激励输入，分别进行Z向12h，X向12h，Y向12h实验。台架实验过程如图8所示。

整体实验完成后，经检查，未发现电池包结构存在裂纹或变形等形式的结构损伤。证明了优化方案的可靠性，也间接证明了优化分析思路的有效性。

5　结语

本文基于随机振动疲劳理论，通过建立电池包有限元模型，从振动疲劳的角度介绍了电池包随机振动疲劳的仿真方法，对于电池包存在疲劳失效风险的情况，进行了理论分析。并提出了改善电池包局部刚度以提升电池包模态频率的优化思路，从仿真结果来看，传递函数最大应力响应的频率范围避开加速度功率谱密度峰值频率区间，可有效降低电池包疲劳失效的风险。最后基于企业实验标准进行台架实验，验证了所提优化方案和优化思路的有效性。

邹宾兴

江铃汽车股份有限公司　江西省南昌市　330052

汽车零部件