广告
基于相平面的车辆稳定性分析与预判
车辆的操纵稳定性包含相互联系的两部分：操纵性与稳定性，指的是车辆的本身属性。车辆作为一个强耦合的非线性系统，在高车速、低附着、大转向及转向制动/加速等极限工况下，当其本身的操纵稳定性不足以保持车辆正常行驶时，则其失去稳定，失稳主要源于轮胎力饱和。研究发现，初始状态在相平面稳定区域的车辆趋向于自行达到稳态行驶，初始状态在相平面不稳定区域的车辆只有通过施加主动控制（如直接横摆力矩控制，DYC）才能达到稳态，否则将会发生失稳。通过车辆稳定性分析的解析法或稳定边界拟合法能够更为准确地判断车辆的运动状态，甚至提前预测失稳的发生，可用于车辆运动失稳风险的实时预报，对于主动安全控制技术的进一步发展有重大意义。
相平面法是一种适用于二阶非线性系统的稳定性分析方法，具体说是一种图解法，其稳定边界需要拟合。本文通过质心侧偏角相平面分析车辆稳定性，在不失准确性的前提下对相平面进行适当简化，以便于实际应用，同时，揭示相平面上车辆稳定区域随行驶状态的变化规律，构造边界方程并进行参数拟合，最终得到一种动态的稳定边界，可用于实际车辆的稳定性预判。
1.质心侧偏角相平面
汽车的航向角由质心侧偏角和横摆角组成，选取质心侧偏角β和横摆角速度 γ两个状态变量便可反映车辆的侧向稳定性。只考虑轮胎部分的非线性特性，本文基于非线性二自由度动力学模型作为相平面分析用的车辆模型，前、后轴轮胎侧向力由UniTire稳态纯侧偏轮胎模型进行表达，以表征被控对象的最基本侧向动力学特性，则非线性二自由度车辆模型可表示为：
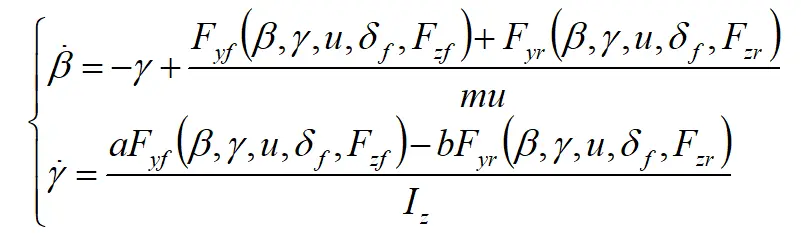
用于车辆稳定性分析的相平面方法主要有：
相平面，
相平面，
相平面。根据非线性二自由度车辆模型可得，
可表达为轮胎侧向力和横摆角速度的函数；另外，与
相平面不同，
相平面内的车辆系统平衡点（奇点）位置在β轴上，即
，便于确定平衡点坐标。
因此，本文选择
相平面进行车辆稳定性分析，以便于划分稳定区域和拟合失稳边界。基于非线性二自由度车辆模型，通过赋予变量β和γ不同的初始状态组合，即可获得完整的相平面图；之后，研究车辆行驶参数对
相轨迹走向的影响；最后，根据奇点位置将
相平面划分为稳定区域和不稳定区域两部分，并结合实际应用对相平面图进行简化。如下图所示，蓝色边界线为车辆的稳定边界，蓝色边界线以内为车辆的稳定区域，蓝色边界线以外为车辆的不稳定区域。
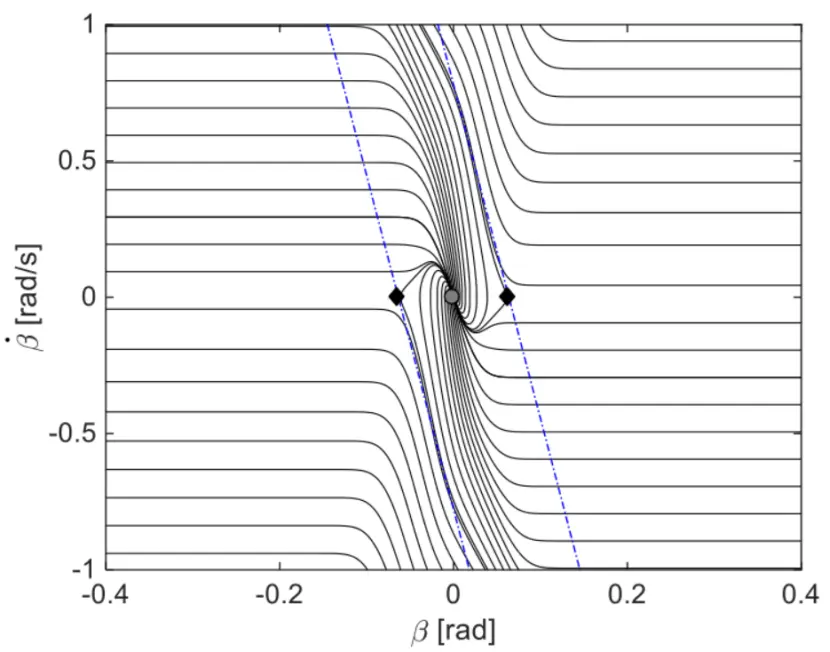
图1 简化的
相平面
2.质心侧偏角相平面
本文提出一种计算简单的边界方程形式，并通过拟合确定方程参数，得到一种车辆稳定性动态辨识方法。将车辆
相平面稳定区域边界近似简化为如图1中所示的两条直线。根据UniTire轮胎模型，当垂直载荷Fz固定时，轮胎侧向力主要由纵向车速u、路面摩擦系数μ及前轮转角δf共同决定。在此基础上，本文研究了u、μ及δf三个输入对
相平面稳定边界的影响，及其影响规律的耦合关系。对稳定边界表达式结构进行改进，并利用曲线拟合工具箱对边界方程函数进行拟合。与现有的
相平面稳定边界描述方法相比，本文提出的方法准确性更高，且建模考虑的行驶工况范围更广，可准确表达车速0~40m/s、摩擦系数0~1及前轮转角0~10deg范围内的边界位置。动态变化的车辆稳定边界拟合公式为
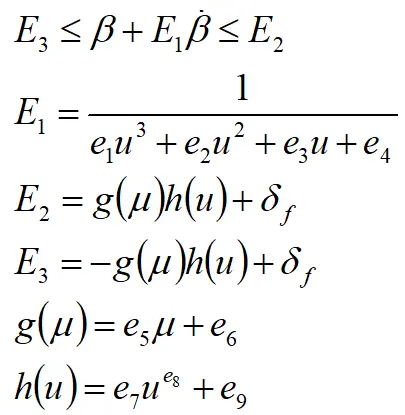
其中，E2和E3代表
图中鞍点的位置，其受u和μ的共同影响；边界参数e1-e9如下表所示。结合图1可以看出，当上述稳定区域边界的斜率及鞍点的位置均为已知时，则车辆稳定区域便得以确定。
表1 边界方程参数e1-e9的值
车辆稳定边界公式中关键参数的拟合值如下图所示。由图可见，车速越大、摩擦系数越小，稳定边界的斜率越小，鞍点位置约靠近稳定零点，则车辆稳定区域越小，车辆行驶风险越大。
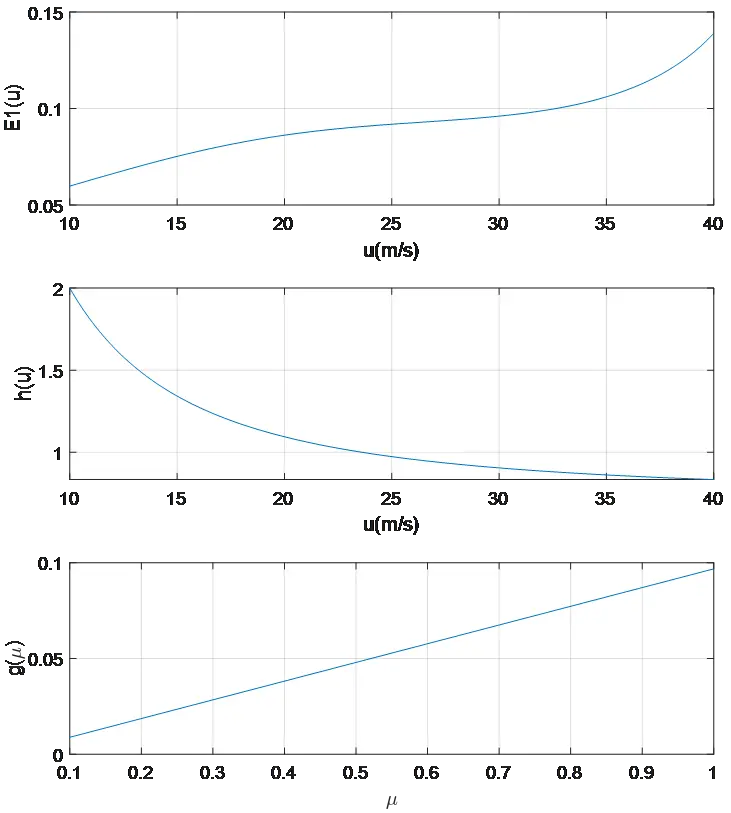
图2 车辆稳定边界公式中关键参数的拟合值
广告
最新资讯
-
高压蒸煮试验在汽车密封性能及组件耐用性评
2024-06-17 09:35
-
温湿度堆码试验在汽车可靠性综合环境测试中
2024-06-17 09:33
-
高度加速应力审计（HASA）在汽车产品寿命评
2024-06-17 08:45
-
新能源汽车用电动压缩机与电子膨胀阀匹配研
2024-06-17 08:43
-
车联网：隐私保护与技术便利的平衡探索
2024-06-17 08:24
广告
广告
