广告
振动实验经常用到的计算公式，建议收藏！
1、求推力(F)的公式
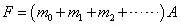
式中：
F — 推力(激振力)(N)
m0 — 振动台运动部分有效质量(kg)
m1 — 辅助台面质量(kg)
m2 — 试件(包括夹具、安装螺钉)质量(kg)
A — 试验加速度(m/s²)
2、加速度(A)、速度(V)、位移(D)三个振动参数的互换运算公式
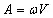
式中：
A — 试验加速度(m/s²)
V — 试验速度(m/s)
ω — 角速度，ω=2πf
f — 试验频率(Hz)
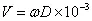
式中：
V — 试验速度(m/s)
D — 位移(mm，0-P)单峰值
ω — 角速度，ω=2πf
f — 试验频率(Hz)
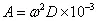
式中：
A — 试验加速度(m/s²)
D — 位移(mm，0-P)单峰值
ω — 角速度，ω=2πf
f — 试验频率(Hz)
上式亦可简化为：
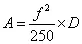
式中：
A — 试验加速度(g，1g=9.8m/s²)
D — 位移(mm，0-P)单峰值
f — 试验频率(Hz)
上式也可以改写为：
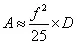
A — 试验加速度(m/s²)
D — 位移(mm，0-P)单峰值
f — 试验频率(Hz)
3、定振级扫频试验平滑交越点频率的计算公式
(1) 加速度与速度平滑交越点频率的计算公式
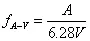
式中：
fA-V — 加速度与速度平滑交越点频率(Hz)
A — 试验加速度(m/s²)
V — 试验速度(m/s)
(2) 速度与位移平滑交越点频率的计算公式
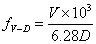
式中：
VD-f — 加速度与速度平滑交越点频率(Hz)
V — 试验速度(m/s)
D — 位移(mm，0-P)单峰值
(3) 加速度与位移平滑交越点频率的计算公式
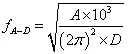
式中：
fA-D — 加速度与位移平滑交越点频率(Hz)
A — 试验加速度(m/s²)
D — 位移(mm，0-P)单峰值
上式可以简化为：
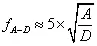
4、扫描时间和扫描速率的计算公式
(1) 线性扫描比较简单：
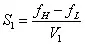
式中：
S1 — 扫描时间(s或min)
fH-fL — 扫描宽带，其中fH为上限频率，fL为下限频率(Hz)
V1 — 扫描速率(Hz/min 或Hz/s)
(2) 对数扫频
倍频程的计算公式：
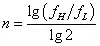
式中：
n — 倍频程(oct)
fH — 上限频率(Hz)
fL — 下限频率(Hz)
扫描速率计算公式：
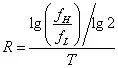
式中：
R — 扫描速率(oct/min或s)
fH — 上限频率(Hz)
fL — 下限频率(Hz)
T — 扫描时间(min或s)
扫描时间计算公式：
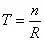
式中：
T — 扫描时间(min或s)
n — 倍频程(oct)
R — 扫描速率(oct/min 或oct/s)
5、随机振动试验常用的计算公式
(1) 频率分辨力计算公式：
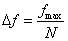
式中：
△f — 频率分辨力(Hz)
fmax — 最高控制频率(Hz)
N — 谱线数(线数)
fmax是△f的整倍数
(2) 随机振动加速度总均方根值的计算
A、利用升谱和降谱以及平直谱计算公式
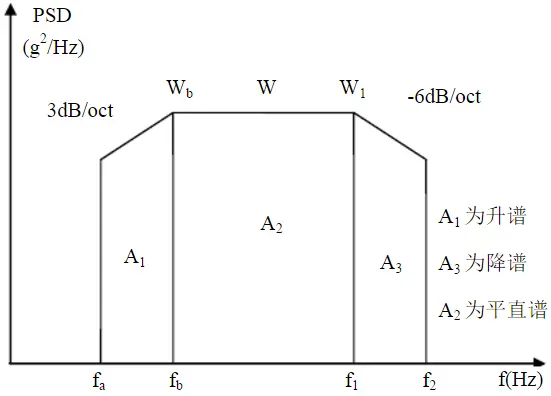
功率谱密度曲线图(a)
平直谱计算公式：
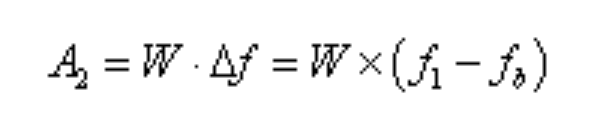
升谱计算公式：
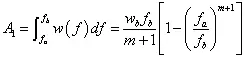
降谱计算公式：
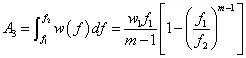
式中：m=N/3，N为谱线的斜率(dB/octive)。
若N=3，则m=1时，必须采用以下降谱计算公式：
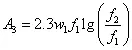
加速度总均方根值：
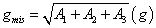
B、利用平直谱计算公式：计算加速度总均方根值
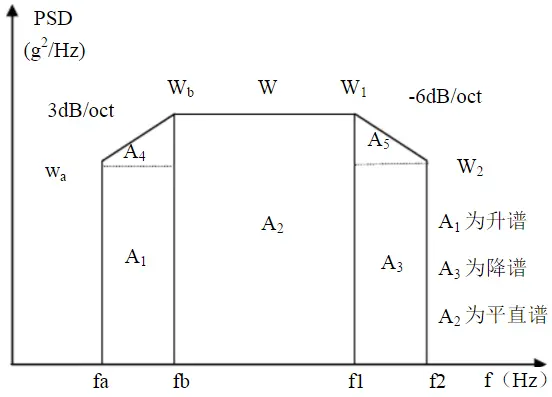
功率谱密度曲线图(b)
为了简便起见，往往将功率谱密度曲线图划分成若干矩形和三角形，并利用上升斜率(如3dB/oct)和下降斜率(如-6dB/oct)分别算出wa和w2，然后求各个几何形状的面积与面积和，再开方求出加速度总均方根值：
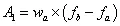
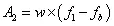
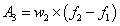
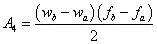
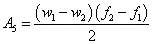
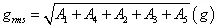
注意：第二种计算方法的结果往往比用升降谱计算结果要大，作为大概估算可用，但要精确计算就不能用。
(3) 已知加速度总均方根g(rms)值，求加速度功率谱密度公式
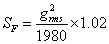
(4) 求Xp-p最大的峰峰位移(mm)计算公式
准确的方法应该找出位移谱密度曲线，计算出均方根位移值，再将均方根位移乘以三倍得出最大峰值位移(如果位移谱密度是曲线，则必须积分才能计算)。在工程上往往只要估计一个大概的值。这里介绍一个简单的估算公式
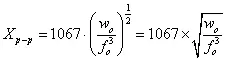
式中：
Xp-p — 最大的峰峰位移(mm，p-p)
fo — 为下限频率(Hz)
wo — 为下限频率(fo)处的PSD值(g²/Hz)
(5) 求加速度功率谱密度斜率(dB/oct)公式
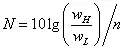
式中：n为oct倍频程
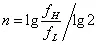
wH — 频率fH处的加速度功率谱密度值(g²/Hz)
wL — 频率fL处的加速度功率谱密度值(g²/Hz)
广告
广告
最新资讯
-
直播｜中国汽研：重型车温室气体企业平均方
2024-11-23 17:42
-
美国FCC正式划定5.9GHz频段用于C-V2X技术
2024-11-23 17:41
-
标准立项 | 《自主代客泊车 预期功能安全测
2024-11-23 16:13
-
长三角（盐城）智能网联汽车试验场气象多级
2024-11-23 16:11
-
CSAE汽车可靠性技术分会第二届委员会第二次
2024-11-23 16:09
广告
广告
