广告
感应电机NVH仿真分析
1. FFT窗函数
（1）Maxwell中的7种窗函数
Rectangular(default)
Triangular
Van Hann
Hamming
Blackman
Lanczos
Welch
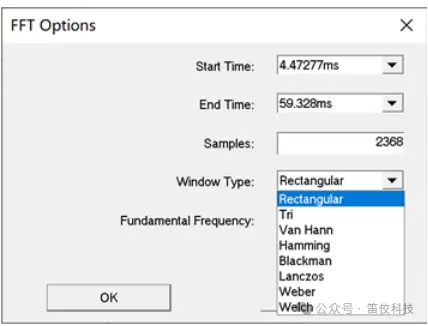
（2） FFT加窗的作用
当信号采样为非整数周期时，FFT会产生本不存在的频率分量(频谱泄露)，而原本幅度比较小的频率分量就可能会被掩盖，加窗的目的就是抑制这些本不该存在频率分量，减小频谱泄露现象。
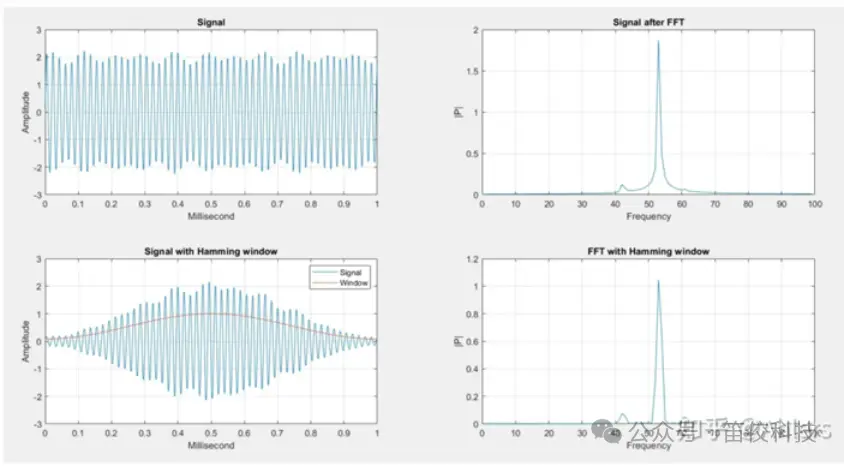
非整数周期信号加Hamming窗
总结：
▪ 加窗会极大缓解FFT的频谱泄露效应，使得频谱泄露只在于附近几个分辨点，且幅度进行了衰减，但无法完全消除；
▪ 其缺点是对时域信号进行了整形，功率进行了衰减，但是其谱线反映的幅度(或者功率)已经不在能表征为原始信号的频率了；
▪ 电机电磁场仿真通常求解整数个电周期，即使是感应电机也可使用稳态检测功能使结果尽量逼近稳态，再获取整数个周期的近似稳态数据，此时频率泄露现象很小，如果对电磁力数据加窗会导致主波幅值下降，频域电磁力的计算结果不准确；
▪ 加窗比较适用于对噪声或振动等时域信号进行短时傅里叶变换STFT。
2. 感应电机电磁力FFT研究
（1）感应电机电磁力分析
感应电机主要电磁力波
▪ 由基波产生
- 2f1
▪ 由定转子齿谐波相互作用产生
- k2*Z2/p*(1-s)*f1+2f1
- K2*Z2/p*(1-s)*f1
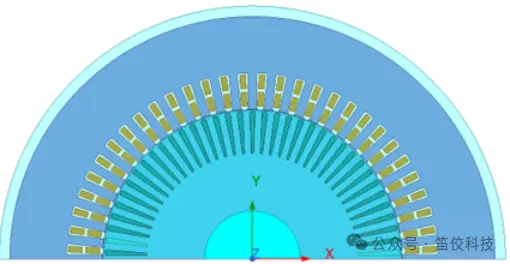
4极，定子60槽，转子74槽
（2）感应电机仿真求解时间设置
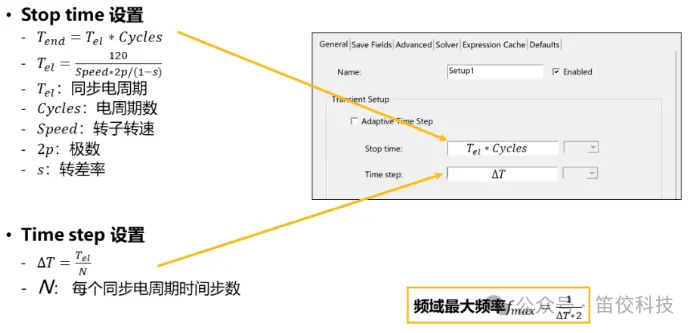
（3）电磁力采样设置
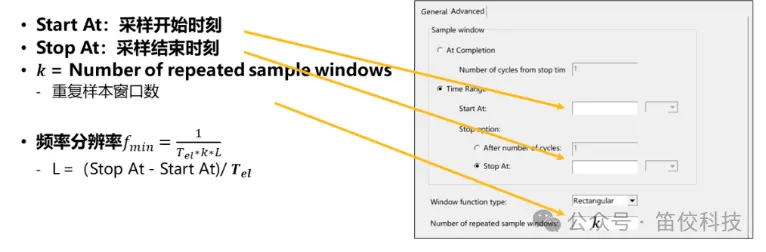
（4）最佳采样周期数研究
▪ 对于感应电机，应令k=1，通过增加L提高频率分辨率
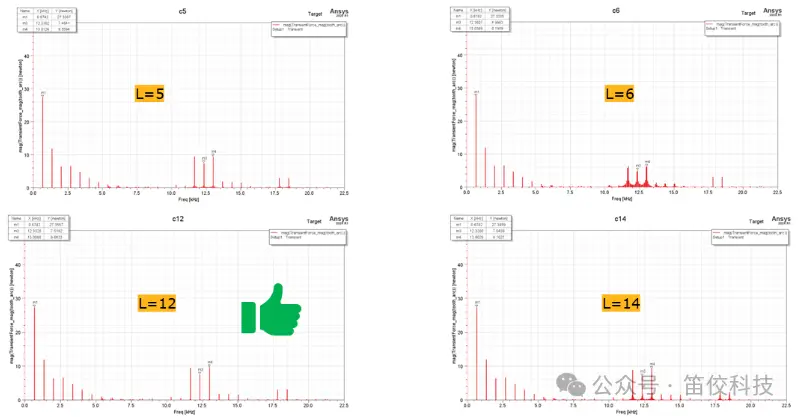
▪ 如需精确捕捉 k2*Z2/p*(1-s)*f1 谐波
-应使k2*Z2/p*(1-s)*f1/fmin = k2*Z2/p*(1-s)*L=n，n为整数
- 由于s为小数，绝大多数情况下，L和n不能同为整数
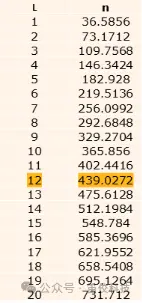
▪ 可通过选择合适的整数L，使n最接近整数
- 高频电磁力计算频率尽可能接近理论计算结果
- 尽可能减小频谱泄露现象
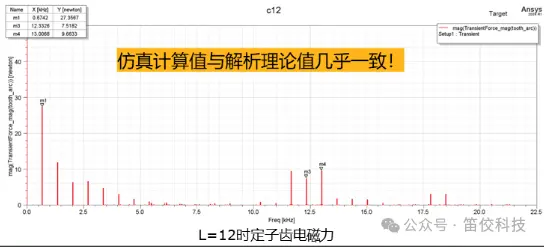
此例中，L=12时，n=439.0272，为L<20以内的最佳值，仿真计算频率:
2f1 =674.2Hz
k2*Z2/p*(1-s)*f1+2f1=13006.8HZ
k2*Z2/p*(1-s)*f1=12332.6HZ
▪ 本例不同转差率s对应的最佳采样周期数L
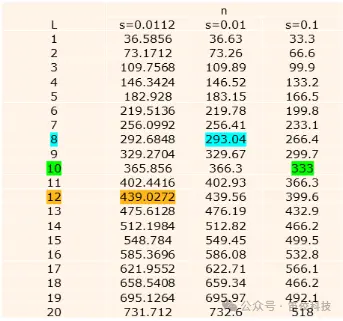
结论
▪ 感应电机仿真时，一般将求解时间设置为同步周期的倍数；
▪ 感应电机关键电磁力谐波频率与转差率相关，且频率较高；
▪ 不同转速工况的转差率不同，最佳采样周期数也不同。
- 注意:计算多转速NVH瀑布图时，由于当前版本的限制，必须设置统一的采样周期数，否则瀑布图阶次是乱的。推荐的采样周期数为:n*p个同步周期(n个机械周期)
3.感应电机NVH案例
（1）感应电机NVH案例
Tesla lDM
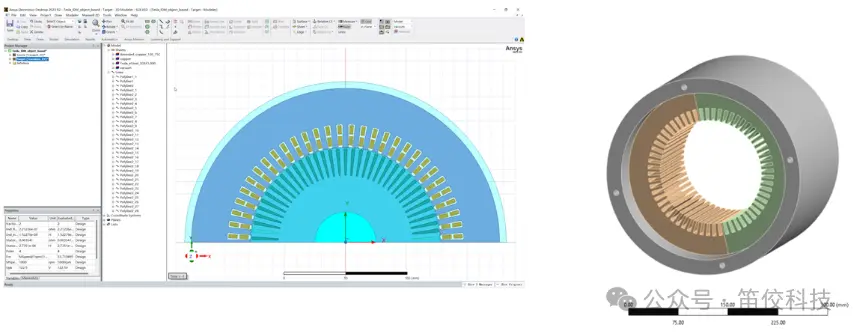
▪ 对转速、电压、转差率参数化
▪ 各个工况点统一计算20个同步周期取最后10个同步周期的结果用于NVH仿真
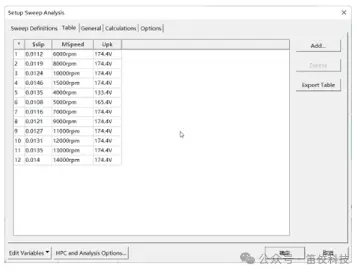
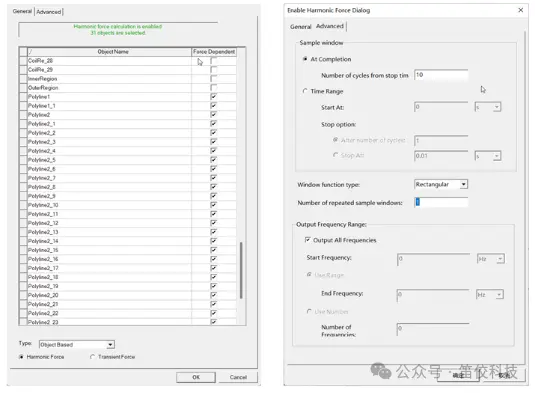
▪ 使用激励波形优化+Source&Target法加速求解多转速稳态工况
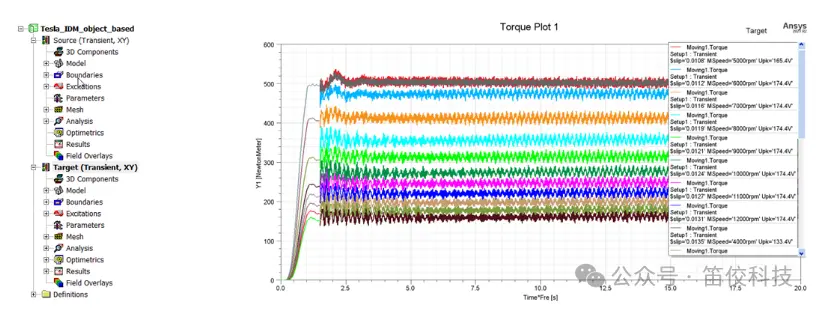
（2）Maxwell 输出XML文件
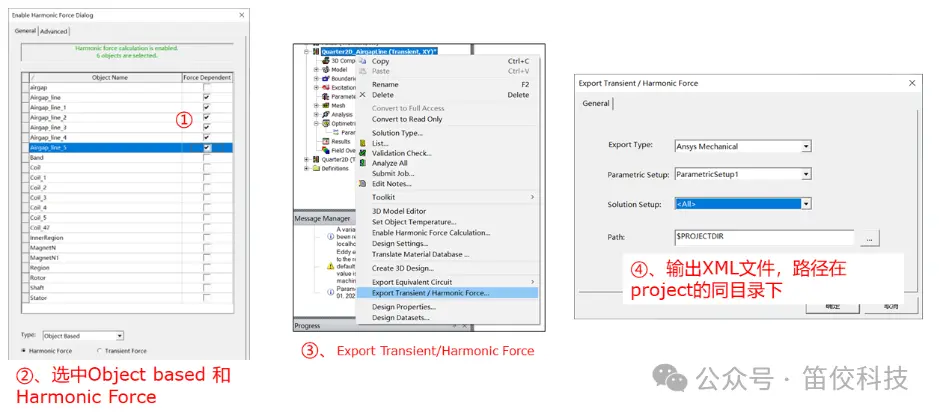
（3）XML文件的查看
▪ 用户可以查看输出的XML文件信息
▪ 文件中包含了NVH分析所需的转速、位置、频率、频率电磁力和转矩的XYZ分量和Re/lm等信息
广告 
广告
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
广告
广告
