寻找供应商
广告
首页 > 汽车技术 > 正文

常见的阻尼类型

2024-06-24 08:10:40·  来源：模态空间  
　

在振动领域中，经常认为阻尼是粘性阻尼，粘性阻尼正比例于运动的速度，又称为线性阻尼。但实际上，振动中的阻尼是一个难点，可能不完全是粘性阻尼。阻尼有不同类型的模型，但对于在一个实际结构中如何计算不同类型阻尼的总效应的知识有限。很多已知类型的阻尼，如库伦摩擦，是非线性的。很多时候，特别是小阻尼时，通过一个线性模型来近似不同类型的阻尼是相对合理的。因而，通常不管结构中的实际阻尼类型，而是使用粘性阻尼来近似。这样的近似是合理的，但除了粘性阻尼之外，还有一些常用类型的阻尼，如迟滞阻尼，也称之为结构阻尼，以及一般阻尼等。


振动领域中普遍采用的粘性阻尼假定阻尼力Fc 与速度 v 成正比，即 



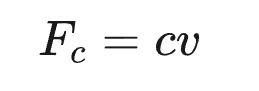
无论是简谐振动还是非简谐振动都可得到线性方程，求解方便，且能方便地表达阻尼对频率、共振等的影响，是应用最为广泛的阻尼模型。对于单自由度系统，使用粘性阻尼获得位移的频响函数（动柔度）为 



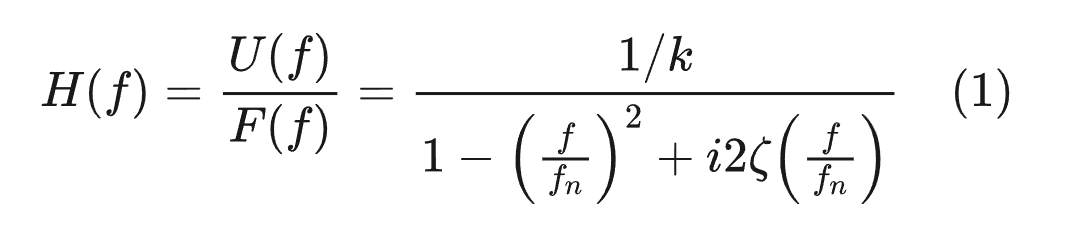
粘性阻尼中的特例是比例阻尼，也经常称为瑞利阻尼，即阻尼矩阵  正比例于质量矩阵  和刚度矩阵   



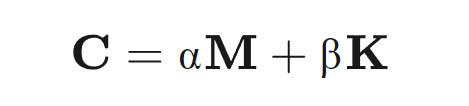
式中，α  和  β是实常数。换句话说，阻尼矩阵是质量矩阵和刚度矩形的线性组合。这是因为材料或结构的实际阻尼机理与质量或刚度相关，对于摩擦而言，阻尼正比例于质量；对于内部材料阻尼而言，阻尼正比例于刚度。因此，如果按瑞利阻尼来考虑，在有限元计算中，只需要输入系数α和β，这样的形式更简单。


我们知道，无阻尼系统的模态求解是一个特征值问题。当使用瑞利阻尼时，同样也是特征值问题，得到的特征向量与无阻尼系统的相同，模态振型为实数。


在机械系统的仿真中，最常用的比例阻尼也称为模态阻尼。对无阻尼系统的每个极点和模态振型添加单个阻尼比，获得模态阻尼。这是因为在有限元动力学方程中，直接构造模态阻尼矩阵非常困难。但如果我们假定阻尼矩阵为比例阻尼形式，即阻尼矩阵可以通过模态向量  正交化为对角阵，即



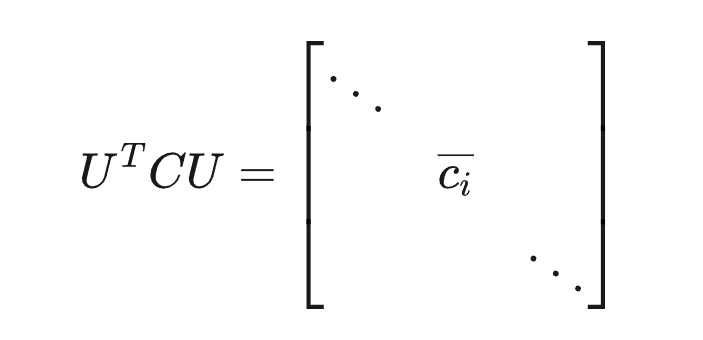
同时，质量矩阵和刚度矩阵也通过模态向量转换成为了对角阵，则动力学方程可以在模态空间进行解耦，将运动方程转化为以模态坐标表示的一系列解耦的单自由度方程。这样，无需直接构建复杂的阻尼矩阵，只需要提供各阶模态阻尼比，然后求解这个单自由度方程，就能得到结构的动力学响应。所以，模态阻尼的本质仍然是粘性阻尼，但它通过定义模态阻尼比来体现粘性阻尼的作用，避免了直接构建阻尼矩阵。


结构阻尼不同于粘性阻尼，它具有频率依赖性，定义如下： 



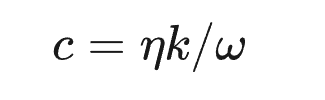
式中，

分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• ENCAP2026对撞后安全的要求（中） • 汽车智能座舱分级与综合评价白皮书
• 一文详解安全分析方法STPA：以自动紧急制动系统（AEB）为 • 新品上市 | Fusion-LN 数据采集的下一个飞跃
• 车规级V2X芯片- 汽车移动通信功能核心 • BEV端到端视觉论文合集|从不同的视角解析BEV感知技术
• 新能源汽车应用中的【夜视系统】与【雨夜系统】 • 汽车安全基础
• 极氪007电驱动系统拆解，看到了啥？ • 长安汽车申请具备单换热器的空调总成的车辆热管理系统专利
0 条相关评论
  • 广告
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026917号-25