【管路】汽车空调低压管路流固耦合振动特性分析

摘要：汽车空调管路的振动与噪声直接影响车内舒适度。基于计算流体力学和结构有限元的流固耦合方法分析了某型汽车空调低压管路系统在制冷剂作用下的振动特性；建立低压管路系统的有限元模型，进行空管模态分析和流体作用下的预应力模态分析，针对橡胶管结构采用分层建模方法进行模态试验验证；使用流体动力学方法分析了制冷剂的流场特性，获取管壁压力，进行流固耦合作用下的管路振动特性分析，分析了流体脉动频率和橡胶管硬度对流致振动特性的影响。结果表明：空调低压管路的模态表现为低频振动的特点，且模态振型主要体现在橡胶管上；考虑制冷剂与管路的流固耦合作用后，模态固有频率增大，最大增加43.83%；靠近压缩机的橡胶管在脉动压力激励下表现出周期性的振动，远离压缩机的橡胶管振动逐渐衰减；管道应力与压缩机工作频率成正相关关系，管道振动位移随着橡胶管硬度增大而减小。

管路模态分析与验证

1.1 空调低压管路

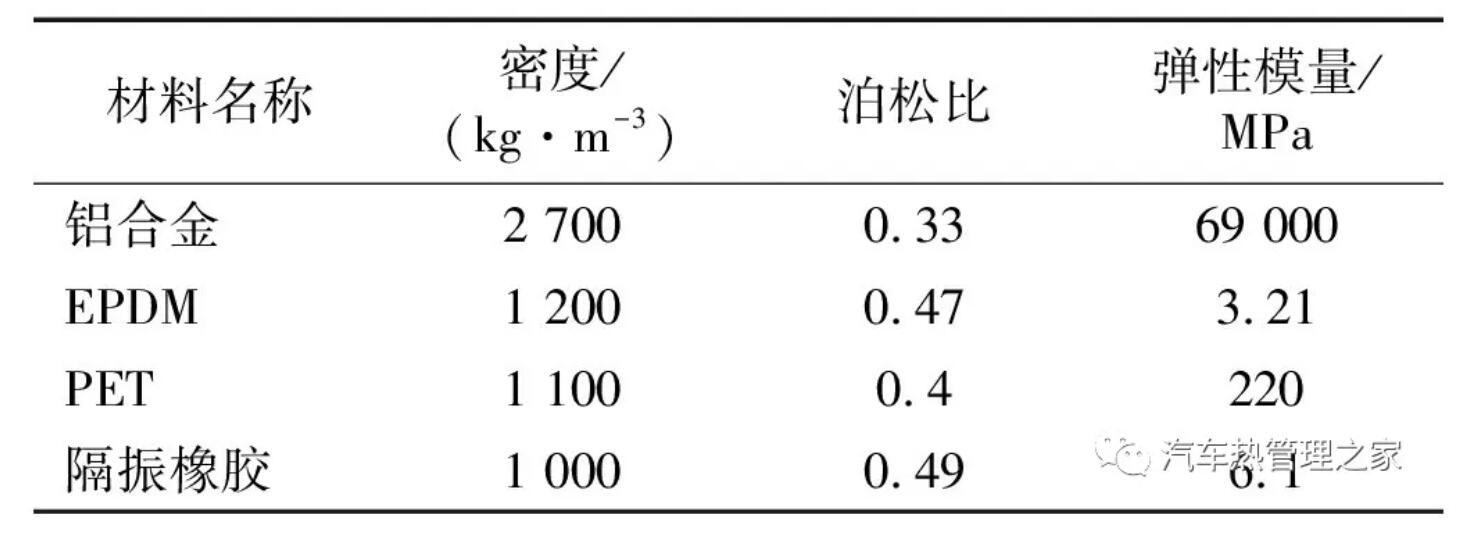
建立空调低压管路三维模型，如图1所示。低压管路系统主要由铝管、橡胶管、消音器、安装支座及隔振橡胶等组成，铝管、消音器和安装支座均为铝合金，橡胶管主体为三元乙丙橡胶材料(ethylene propylene diene monomer,EPDM)，内含聚酯纤维编织层(polyethylene terephthalate,PET)，各材料具体参数如表1所示，本构关系为线弹性模型。低压铝管的内径为13 mm，外径为16 mm；橡胶管厚度为3.5 mm。管道左端连接蒸发器出口，右端连接压缩机入口。

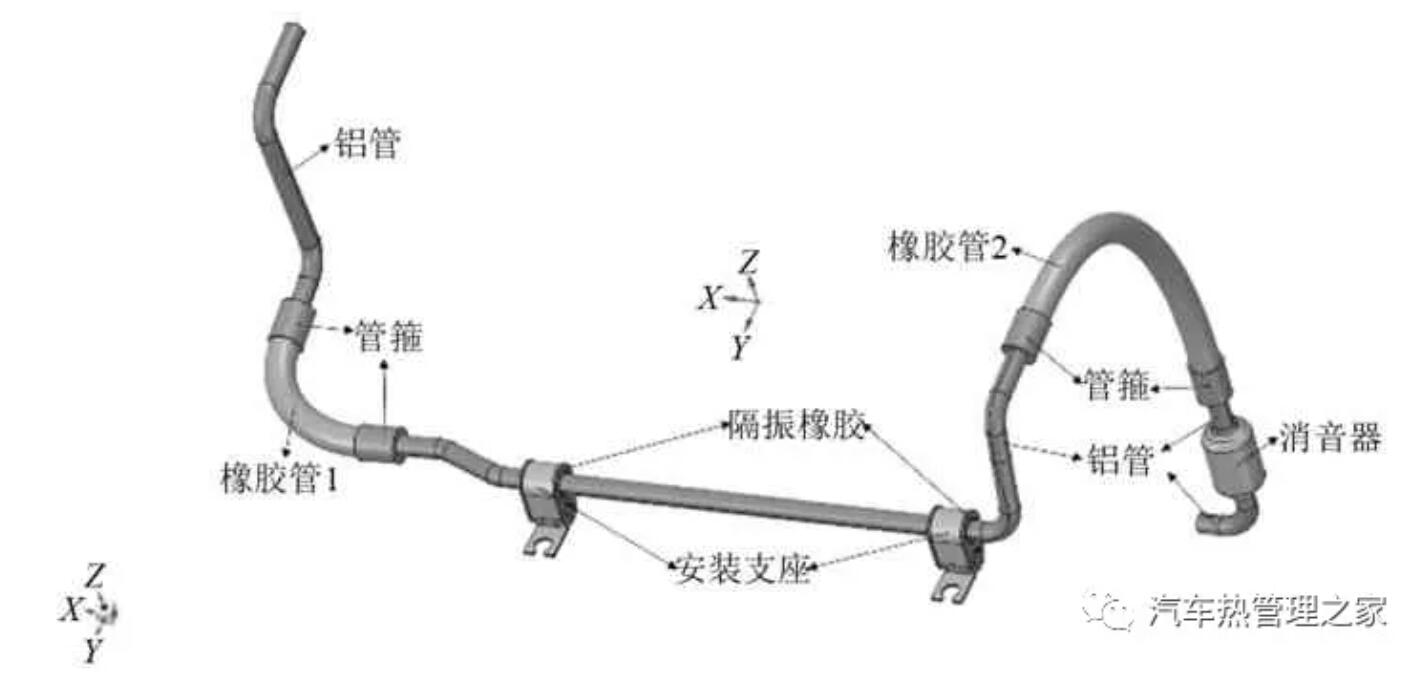
图1 空调低压管路三维模型

表1 空调管路材料参数

1.2 橡胶管2模态分析与试验验证

汽车空调橡胶管是具有多层结构的细长柔性管，主要由两层橡胶和一层聚酯纤维编织层组成，PET编织层的主要作用是防止管路在内部压力作用下发生过度径向膨胀，橡胶管具体结构如图2所示。为保证分析的可靠性，将橡胶管进行分层建模，选取橡胶管2以及相连的两段铝管进行模态试验验证。

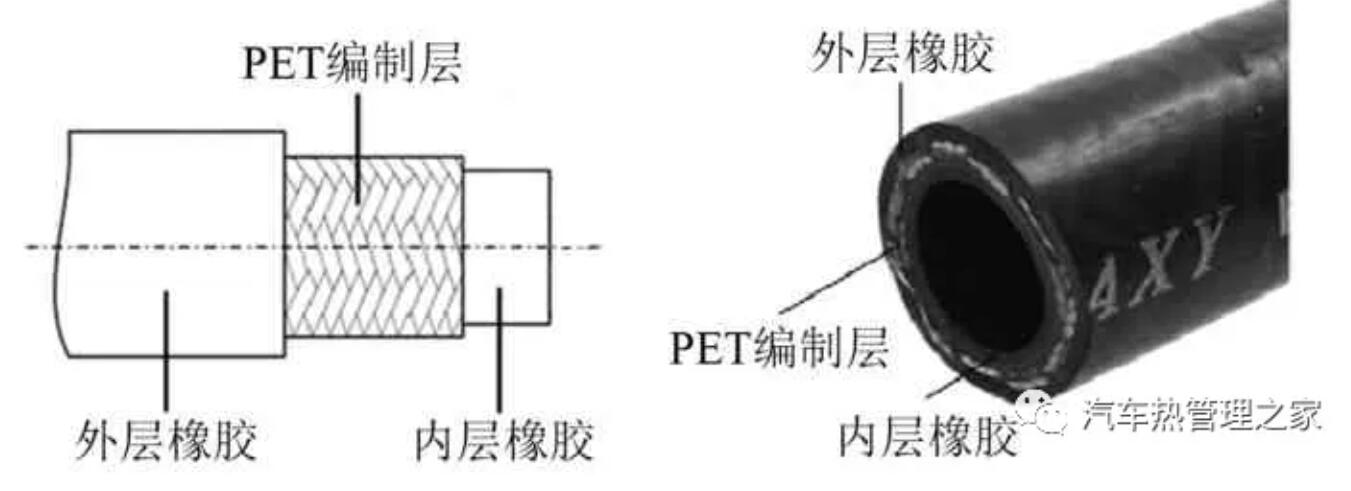
图2 橡胶管结构示意图

橡胶管模态试验分析采用LMS SCR02型16通道数据采集器和LMS Testlab模态测试软件，试验方法为移动加速度计法，传感器类型为BK 4524B三轴加速度传感器。模态试验现场如图3所示，在管道轴向上选取了7个测试点测量结构振动响应，得到频率响应函数如图4所示。

图3 模态试验现场图

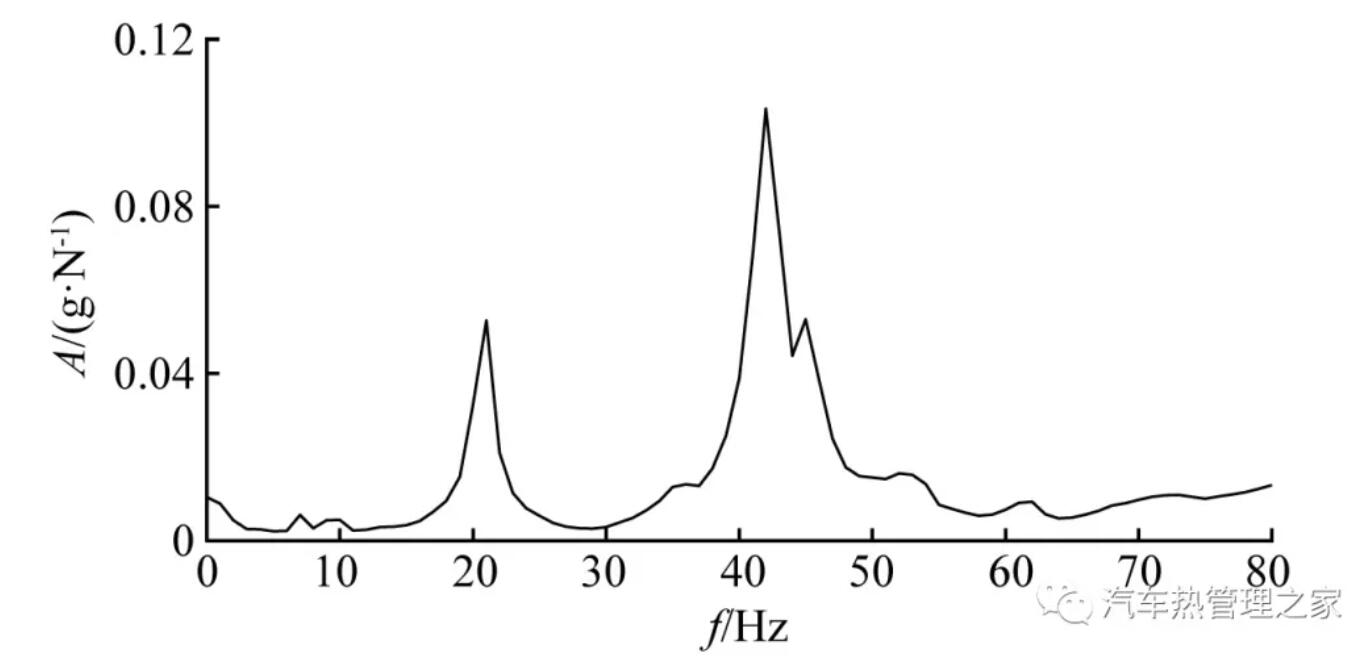
图4 橡胶管频率响应函数

对橡胶管2及相连的两段铝管进行有限元建模，边界条件与模态试验一致，模态仿真和试验结果如表2和图5所示。结果表明有限元计算结果和试验结果吻合较好，固有频率误差在9%以内，最大相对误差为8.75%，并且模态振型也基本一致。证明了橡胶管建模方法的可行性与准确性。

表2 橡胶管固有频率对比

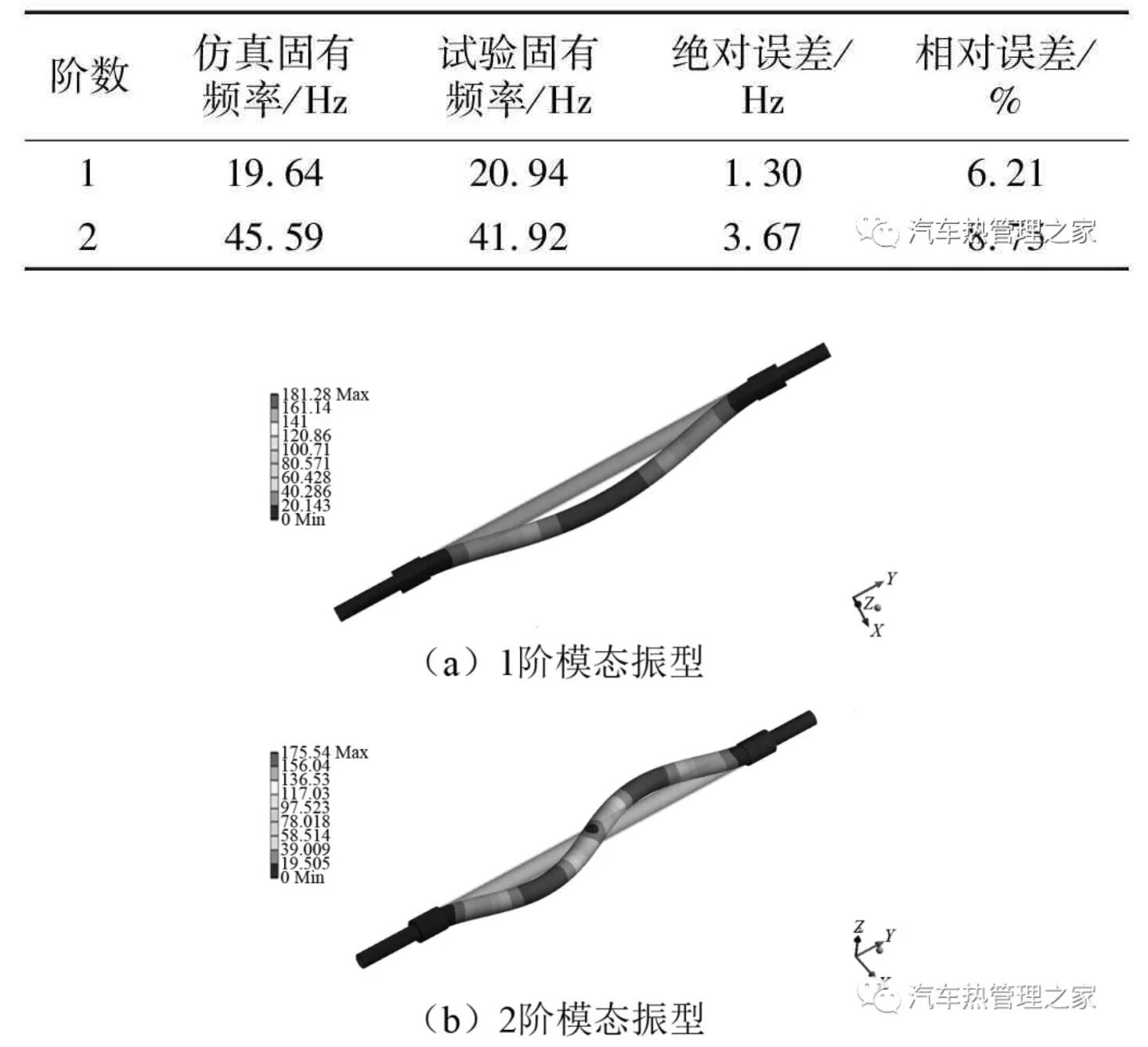
图5 橡胶管模态振型对比

1.3 低压管路模态仿真分析

建立整个低压管路有限元模型，对安装支座内圆面和管道两个端面进行固定约束，采用子空间法对空调管路进行约束模态求解，提取得到前14阶模态参数，固有频率如表3所示。

表3 空调管路固有频率

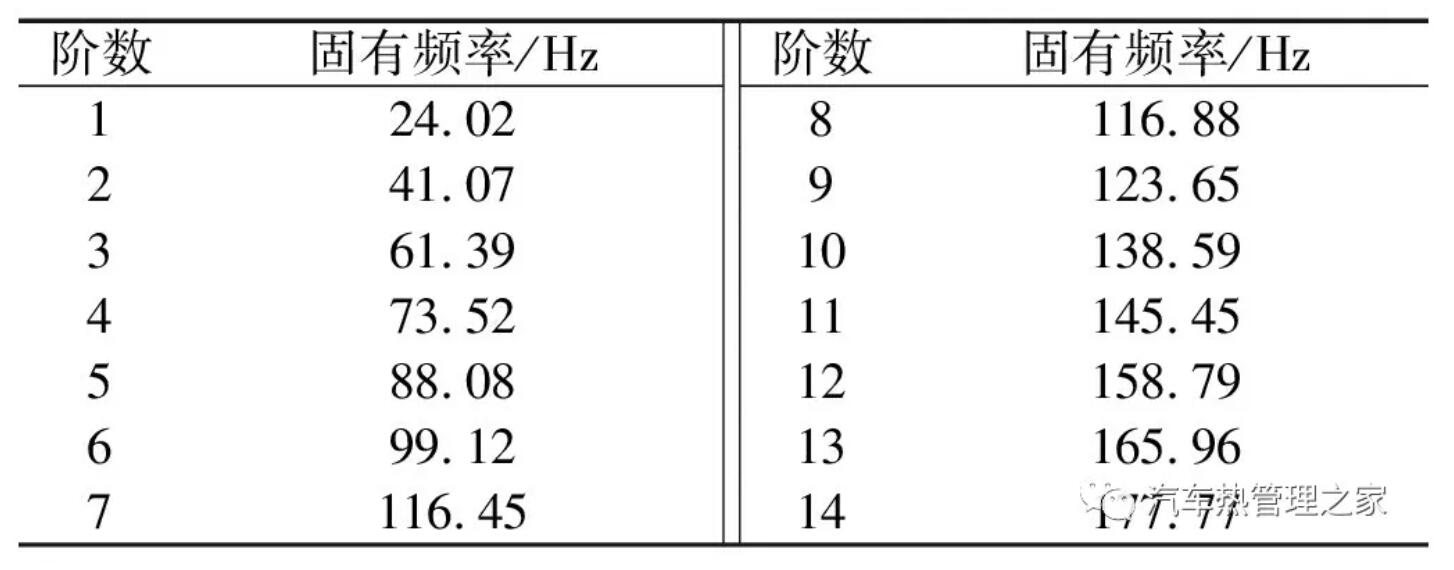
由表3可知，管路前6阶固有频率小于100 Hz，表现出低频振动的特点，管路很容易在外界激励下引起共振。空调低压管路前4阶模态振型，如图6所示。图6中：1阶振型表现为橡胶管2在X方向的摆动；2阶振型为橡胶管2沿Y方向的一阶弯曲；3阶振型为橡胶管2沿X方向的2阶弯曲;4阶振型为橡胶管1在Z方向上的摆动和橡胶管2沿X方向的2阶弯曲。在低频激励下，空调低压管路系统的振动主要体现在橡胶管上，尤其是橡胶管2，这是由于橡胶管自身材料偏软和橡胶管2具有较小的曲率半径所引起的。

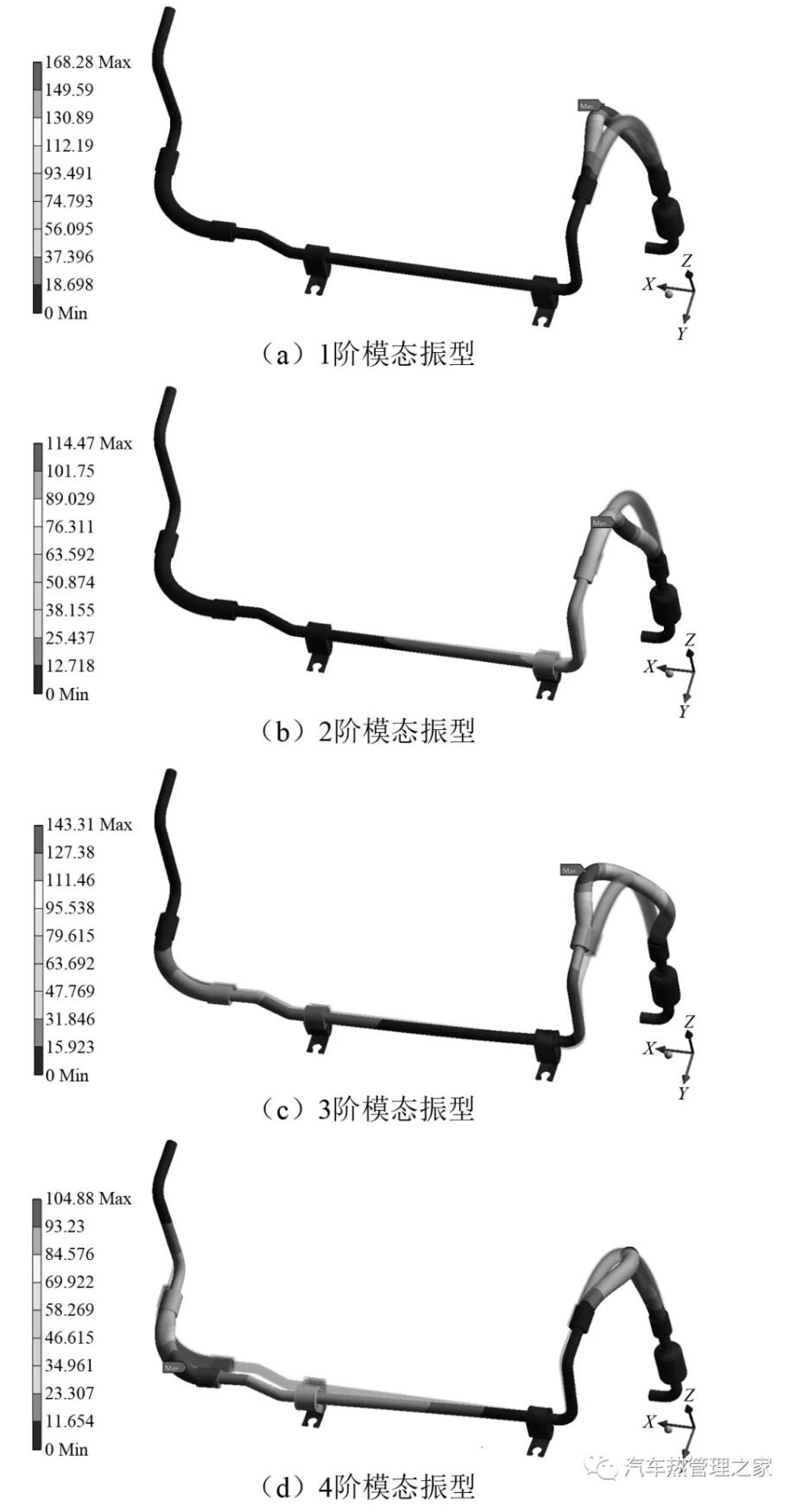
图6 管路模态振型

流体动力学分析

汽车空调系统工作时，在压缩机的吸排气作用下制冷剂在管路内循环流动，流体的压力和内部冲击会导致管路系统的振动，对流体区域进行流体动力学求解，分析内部流动情况，进一步分析流体和管路的相互作用。

2.1 流体网格划分

提取低压管路内部流道，建立流体动力学模型，流体网格单元为四面体，单元类型为Fluid30，为了获得准确的流场特性和壁面压力，进行边界层网格划分，第一层网格厚度为0.026 mm，增长率为1.2，总层数为5层。流体网格对流场计算结果影响较大，为了保证计算的精度以及协调计算时间，对出口流量和出口平均流速进行监测，得到不同单元尺寸下的流场计算结果，如表4所示。

表4 网格无关性验证

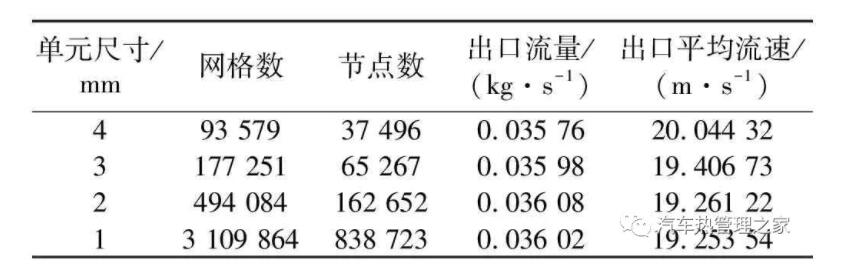
从表4中可知，1 mm和2 mm网格单元尺寸下流场的出口流量和出口平均速度已经基本稳定，差值均小于0.2%，满足网格无关性的要求，为了减少计算时间，网格单元尺寸选择2 mm，最终生成的网格数约为50万，流体网格模型如图7所示。

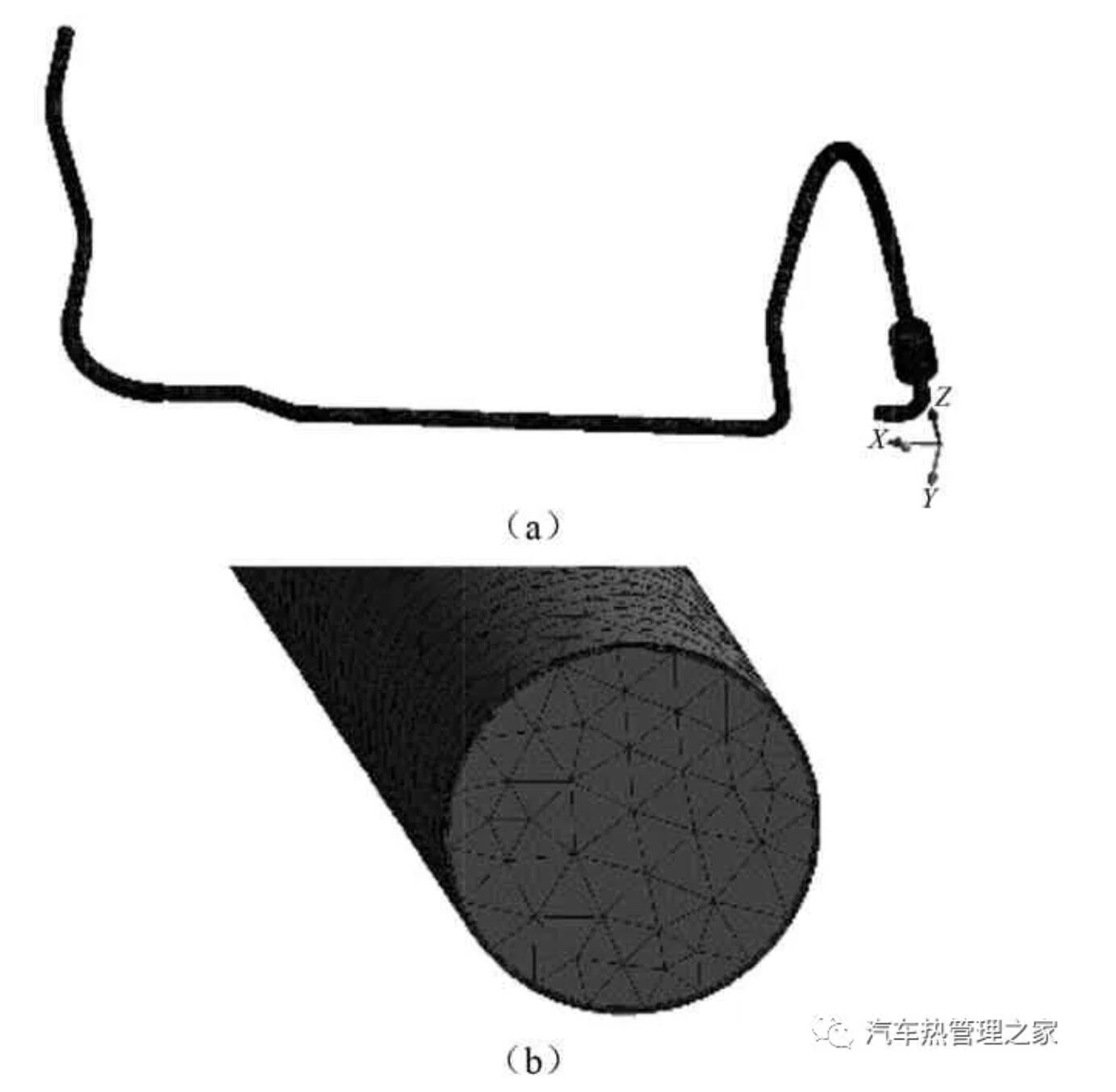
图7 流体网格模型

2.2 边界条件和物理条件设置

汽车空调低压管道左端连接蒸发器出口，设为质量流量入口，根据实车台架测试得到制冷剂质量流量为0.036 kg/s。管路右端连接压缩机入口，由于压缩机间歇性的吸气与排气，管道内的制冷剂速度和压力也会产生周期性的变化。空调低压管内的压力平均值为0.2 MPa，压缩机的最大压力不均匀度为5%，由式(1)可以求得压力脉动幅值ΔP=0.005 MPa。

式中：δ为压力不均匀度；Pmax为最大压力值;Pmin为最小压力值;P0为压力平均值。

非定常压力值记为P(t)，设其为关于时间的正弦函数，表达式为

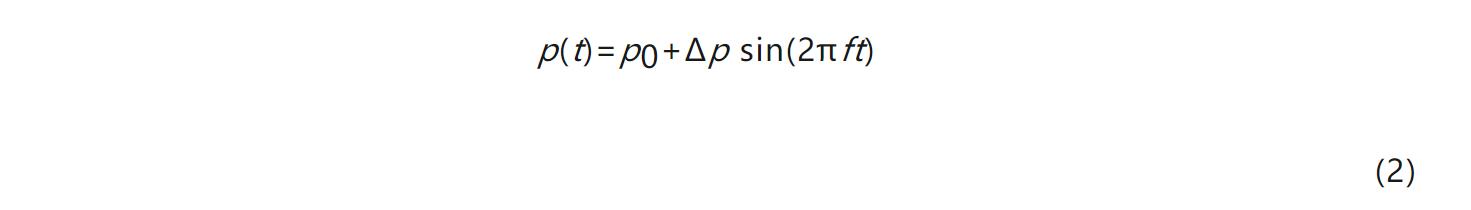
式中：P0为平均压力值；ΔP为压力脉动幅值；f为气流脉动频率，可由式(3)进行计算。

式中：n为压缩机转速；i为压缩机叶片数量。

通过用户自定义函数(user defined function，UDF)进行编辑，得到出口(即压缩机入口)压力脉动函数曲线，如图8所示。

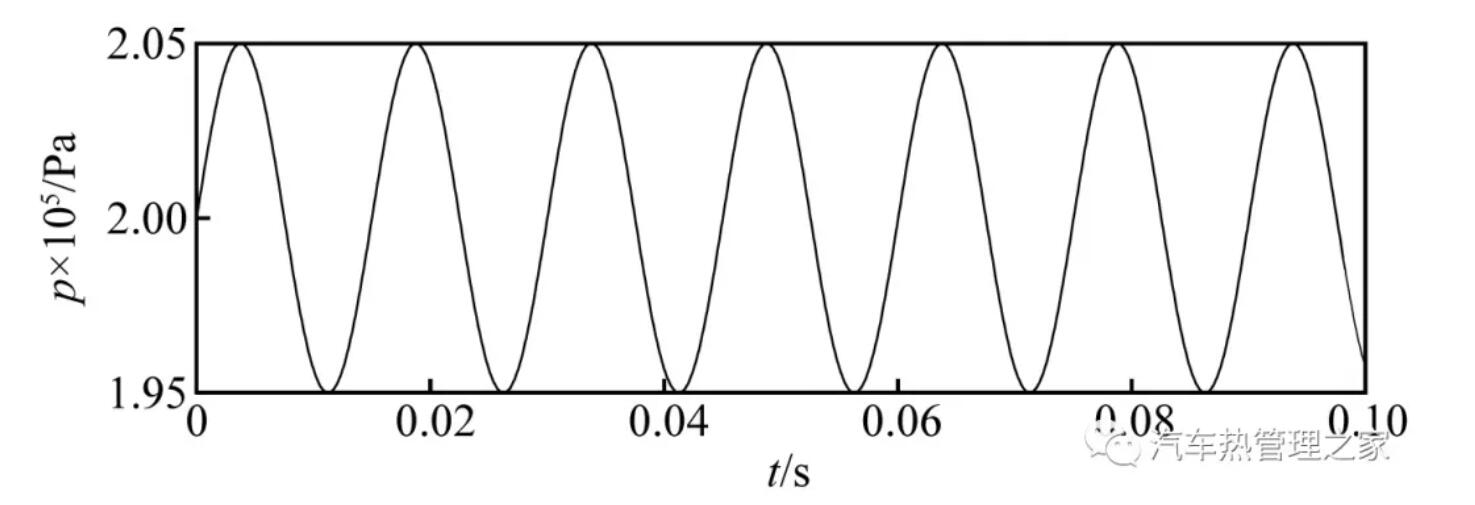
图8 出口压力边界示意图

制冷剂种类为R134a，密度为14.457 kg/m3，动力黏度为1.09×10-5 Pa。管内流动雷诺数Re为1.96×104，为典型的湍流流动，湍流模型选用Realizable k-ε模型，采用Coupled耦合求解算法，空间离散采用First/Second Order Upwind格式。

2.3 流动特性分析

流体动力学分析得到管内流动情况和壁面压力，分别如图9和图10所示。从流动速度矢量云图可知(见图9)，直管段的流体速度较为稳定，而在管路的弯头处出现明显的加速，最大流速达到26.63 m/s，特别是外壁面受到较大的流体冲击，这也是流体引发管道振动的主要原因；橡胶管段由于直径增大流体速度得到一定程度的减小；消音器的扩张效应使得流体速度大幅减小，并出现部分回流现象，流动状态较为紊乱。从壁面压力云图可知(见图10)，平均压力在0.2 MPa左右，最大压力出现在入口段，在流体作用下弯头外侧压力高于内侧，由于压力损失的存在，出口段的压力略低于入口段。

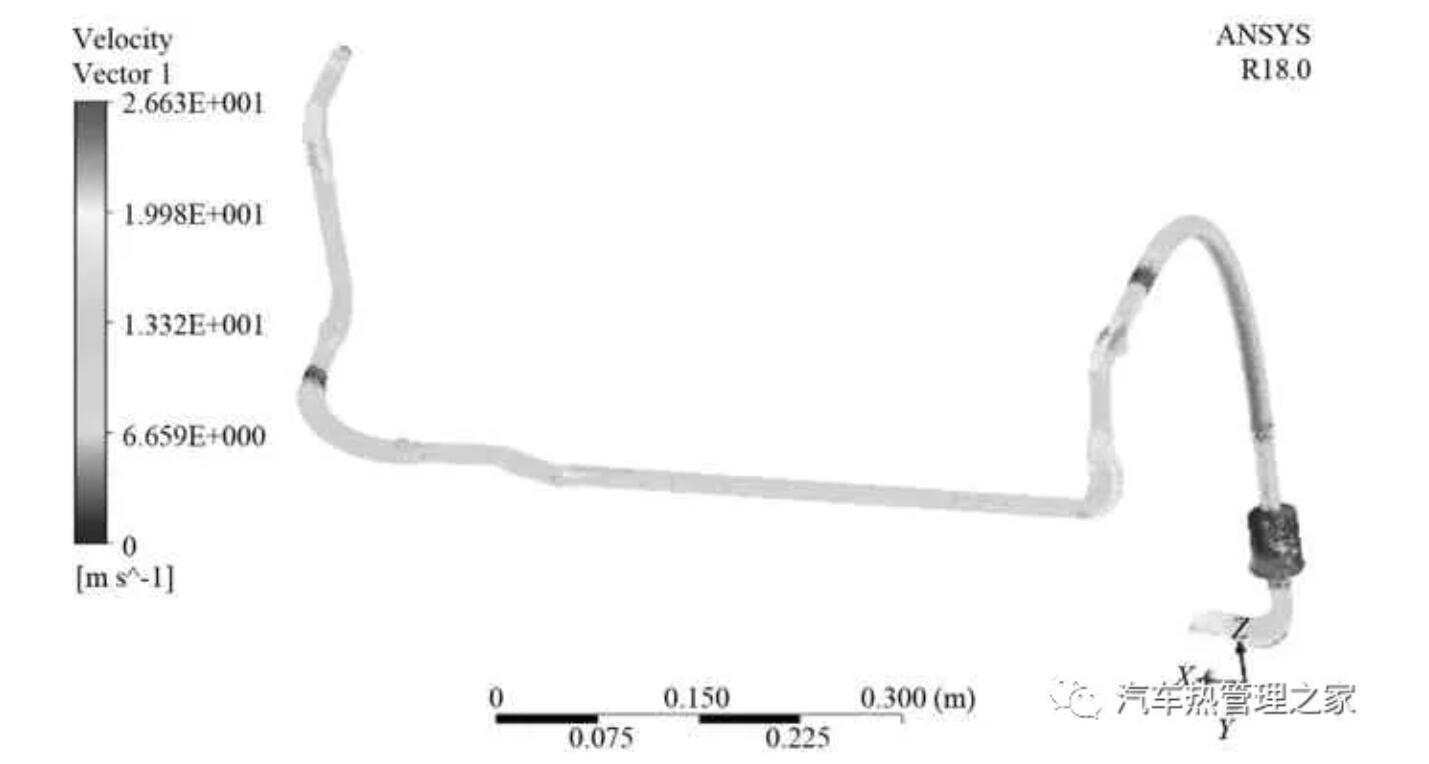
图9 流体速度矢量云图

图10 壁面压力云图

流固耦合振动特性分析

流固耦合问题分为直接求解法和分离求解法，在实际工程应用中通常采用分离求解法。流体区域与固体区域之间通过流固耦合(fluid structure interface,FSI)交界面进行数据的传递，需要满足基本的守恒定律，即交界面处的热流量、温度、位移、应力等参数相等。

3.1 流体激励预应力模态分析

空调低压管路内部充满气态R134a制冷剂，制冷剂的流动和压力会对管路内壁产生冲击。通过流体动力学分析获取流体表面压力，然后通过FSI进行数据传递，进行制冷剂压力下的管路静力学和预应力模态分析，仿真结果如表5所示。从表5可知，在考虑制冷剂对管路的冲击和压力后，各阶固有频率明显提高，最大变化率发生在第1阶固有频率处，为43.83%，这是因为在流体作用下加入了预应力刚度矩阵，使得管路结构等效刚度增大，并且等效刚度的变化大于管路质量的变化。因此，在空调管路的结构振动分析中，应当考虑内部流体作用对管道固有频率的影响。相比之下各阶模态振型变化不大。

表5 固有频率对比Tab.5 Comparison of nature frequency

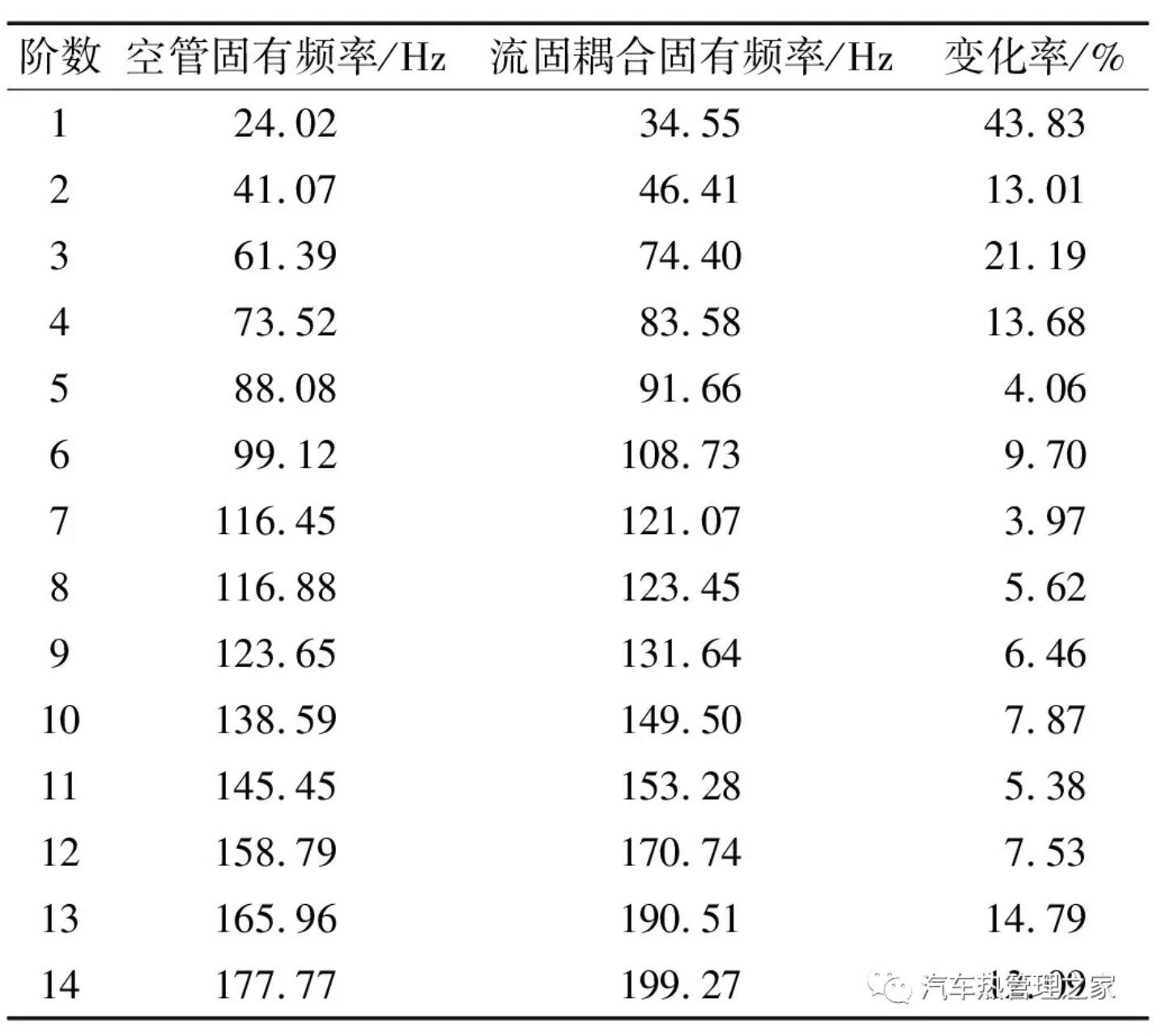
3.2 流体激励谐响应分析

为进一步分析管路在制冷剂冲击和压力作用下的振动特性，进行了空调低压管路的谐响应分析。分析方法选用基于流固耦合模态分析结果的模态叠加法，激振幅值为0.2 MPa，分析频率带宽为0～200 Hz，包括了管路前14阶固有频率；管路阻尼比为0.03，该值广泛用于流固耦合系统和包含橡胶件的结构振动系统。由于橡胶管材料比铝管更软，在制冷剂的压力作用下更容易发生变形和剧烈的结构振动，因此提取橡胶管1和橡胶管2的频率响应曲线，如图11和图12所示。

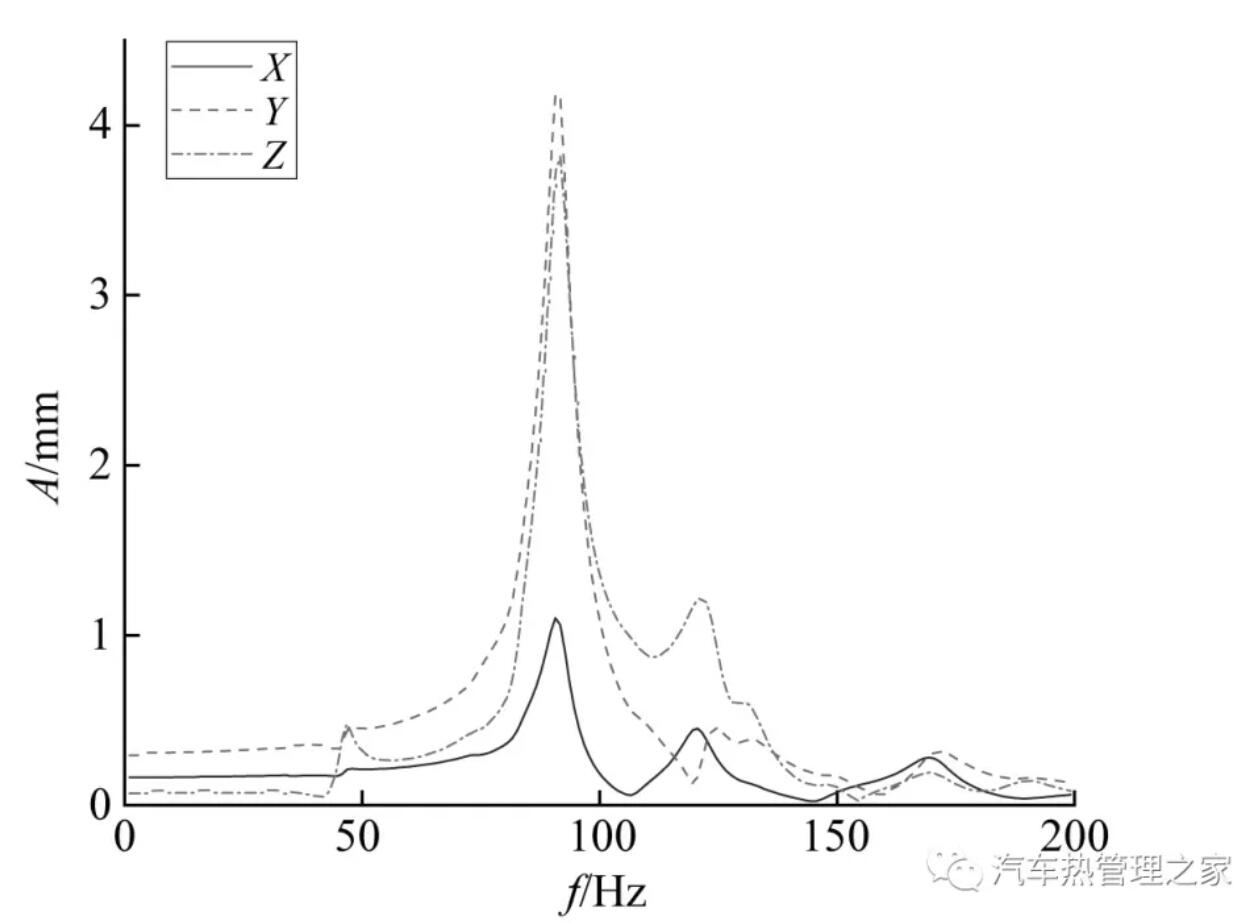
图11 橡胶管1振动特性频率响应曲线

从图11可知，在考虑流固耦合作用后，橡胶管1在管路的第5阶固有频率(91.66 Hz)附近发生了明显的结构共振现象， Y方向的振动位移最大为4.18 mm，其次是Z方向为3.82 mm，X方向为1.09 mm。由图12可知,橡胶管2的振动主要发生在第2阶固有频率(46.41 Hz)附近，具体表现为Y方向上的振动位移达到8.74 mm，其次是Z方向为2.43 mm，X方向为1.22 mm。结果表明：当激励频率在第2阶和第5阶固有频率附近时，管路会发生剧烈的结构共振现象，在工作中应使激励频率尽量远离这两阶固有频率；橡胶管1在X和Y方向上的振动特性比较明显，而橡胶管2的振动主要体现在Y方向上，这与管路的走向和制冷剂的流动方向有关，在管路系统的设计和结构优化中可以考虑增加Y方向上的约束条件，减小振动；同时，橡胶管2与橡胶管1相比振动更加剧烈，这是由于橡胶管2的管长更大，并且具有更小的曲率半径。因此，在进行空调管路的设计与布置时，应当充分考虑管路的长度以及走向，合理增大曲率半径。

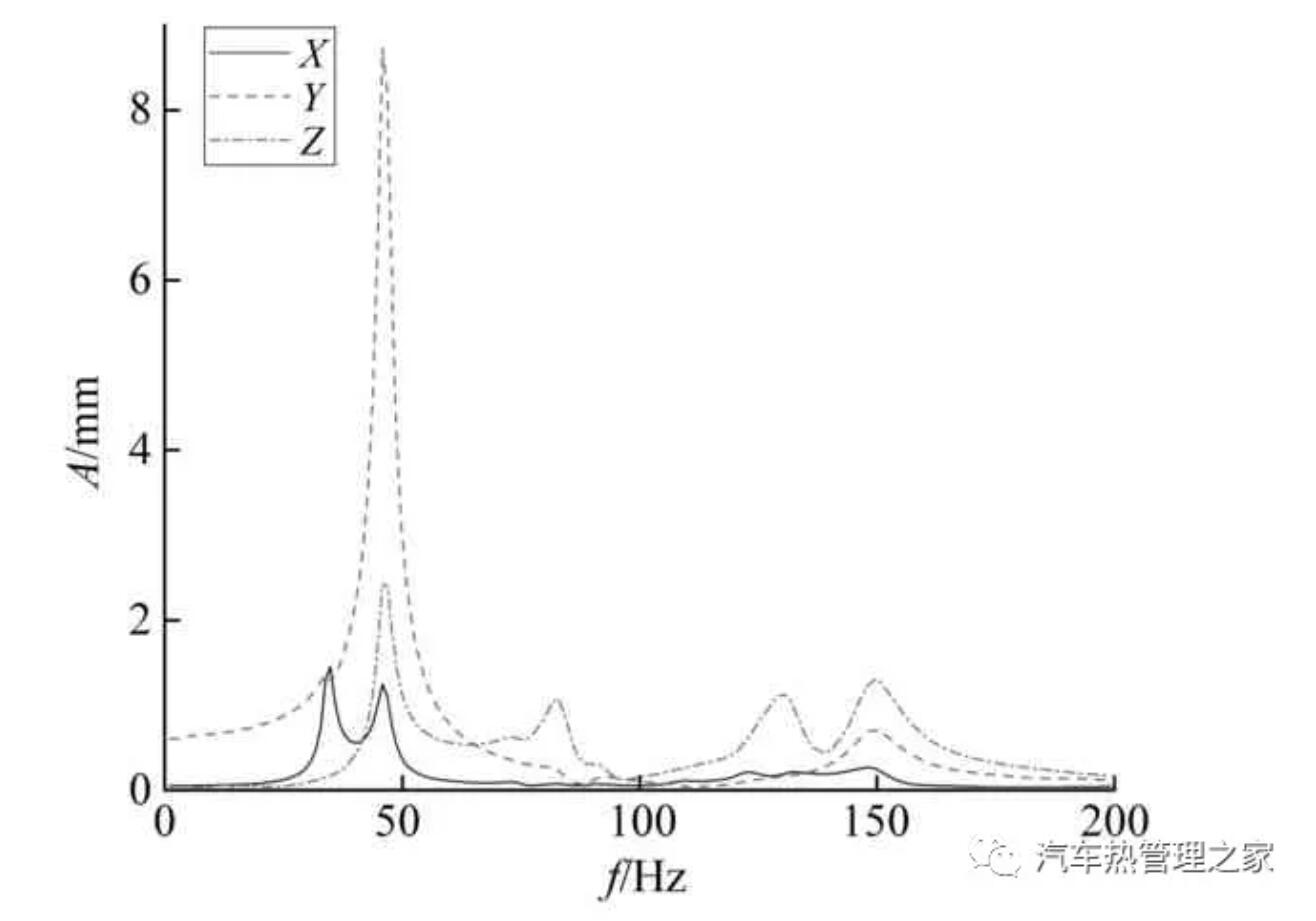
图12 橡胶管2振动特性频率响应曲线

3.3 脉动频率对管路流固耦合振动的影响

汽车空调系统工作时，压缩机转速随着发动机工况的改变也会发生动态变化。为了分析压缩机不同工作频率下的制冷剂流动状态和管路振动特性，压缩机实际工作转速800 r/min,1 200 r/min和1 500 r/min时，由式(3)可求得对应流体脉动频率分别为66.67 Hz，100 Hz和125 Hz，分别进行流固耦合动态仿真。在流固耦合交界面上布置监测点得到特征点压力时间历程曲线，如图13所示。并提取管道振动响应，如图14所示。

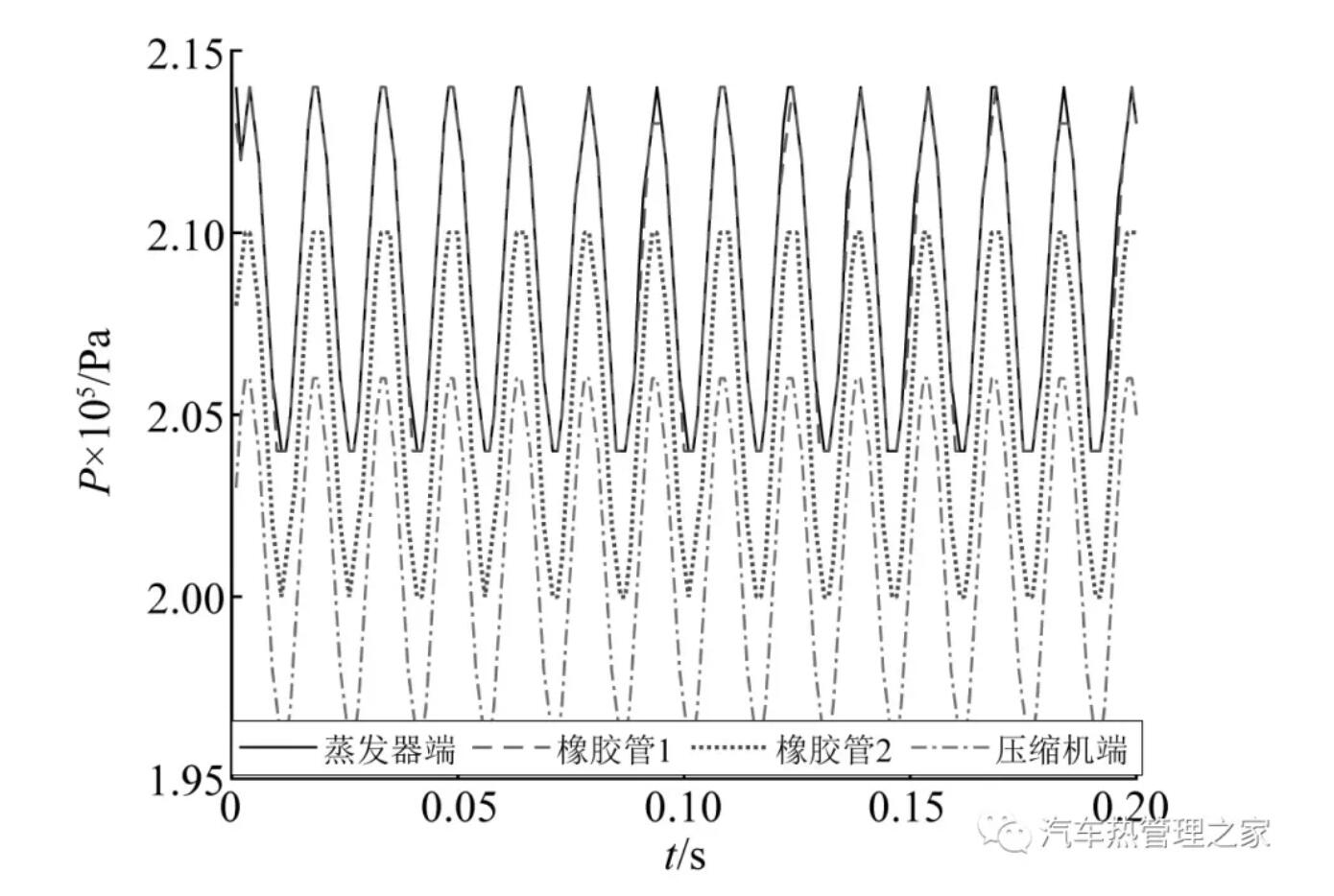
图13 特征点壁面压力图(66.67 Hz)

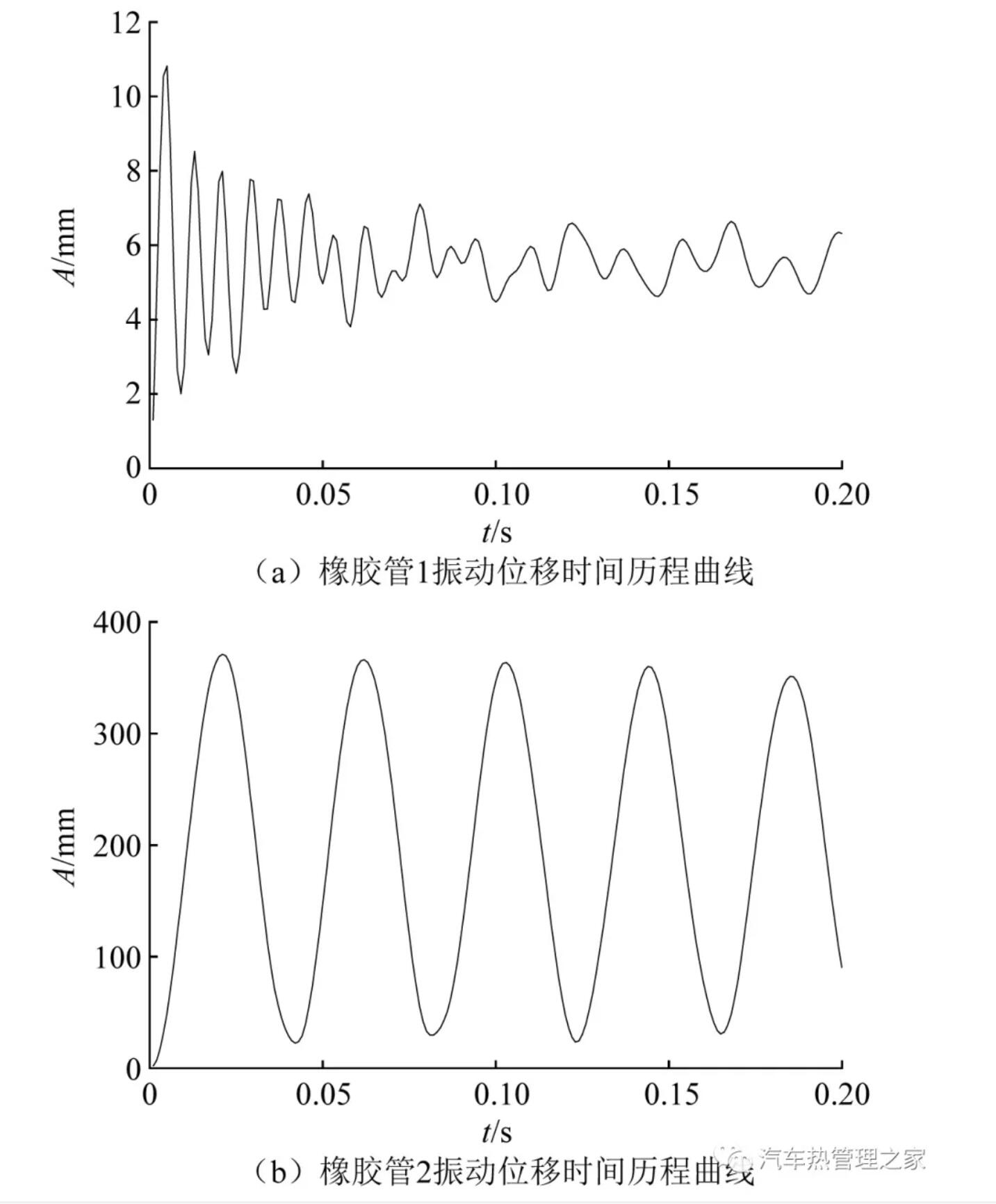
图14 管道流固耦合振动位移结果(66.67 Hz)

从图13中可知，随着压缩机周期性的吸排气，管道特征点的壁面压力也整体表现出周期性的波动，且脉动频率与压缩机工作频率一致。在靠近蒸发器端，管道壁面压力最大，在靠近压缩机端时，压力值降为最小，这与前面制冷剂流动特性分析结果一致，由于流动过程中压力损失的存在，管道壁面压力呈现出整体下降的趋势，但是压力脉动规律不变。

从图14可知，橡胶管1的最大振动位移为10.816 mm，由于橡胶管1远离压缩机，整体位移表现为衰减趋势，并在0.08 s后趋于稳定，平均值为5.53 mm。而靠近压缩机的橡胶管2振动表现得非常明显，整体表现为周期性的位移波动，峰值位移达到371.13 mm，位移均值为196.75 mm。表明在压缩机的周期性压力脉动下，空调管道的振动响应表现出不同的特点，相比之下橡胶管2的振动更加明显和剧烈，原因主要有两点：①橡胶管1离压缩机较远，而橡胶管2靠近压缩机，更容易受到压缩机的脉动激励影响，因而表现出较强的周期振动特性；②橡胶管2比橡胶管1的管长更长，两侧的安装支撑更远，所以在内部制冷剂的冲击下振动更加剧烈。

为了分析压缩机工作频率对管道振动特性的影响，提取了不同脉动频率下管道的应力响应，如图15所示。从图15可知，流体脉动频率对管道应力有着直接的影响，随着脉动频率的增大，管道应力均呈现上升的趋势，并且连接压缩机的管道应力明显大于其他管道。因此在空调管路的结构分析中，不能忽略制冷剂压力脉动对管路的振动响应影响，此外，压缩机附近的管道应当是重点分析的对象。

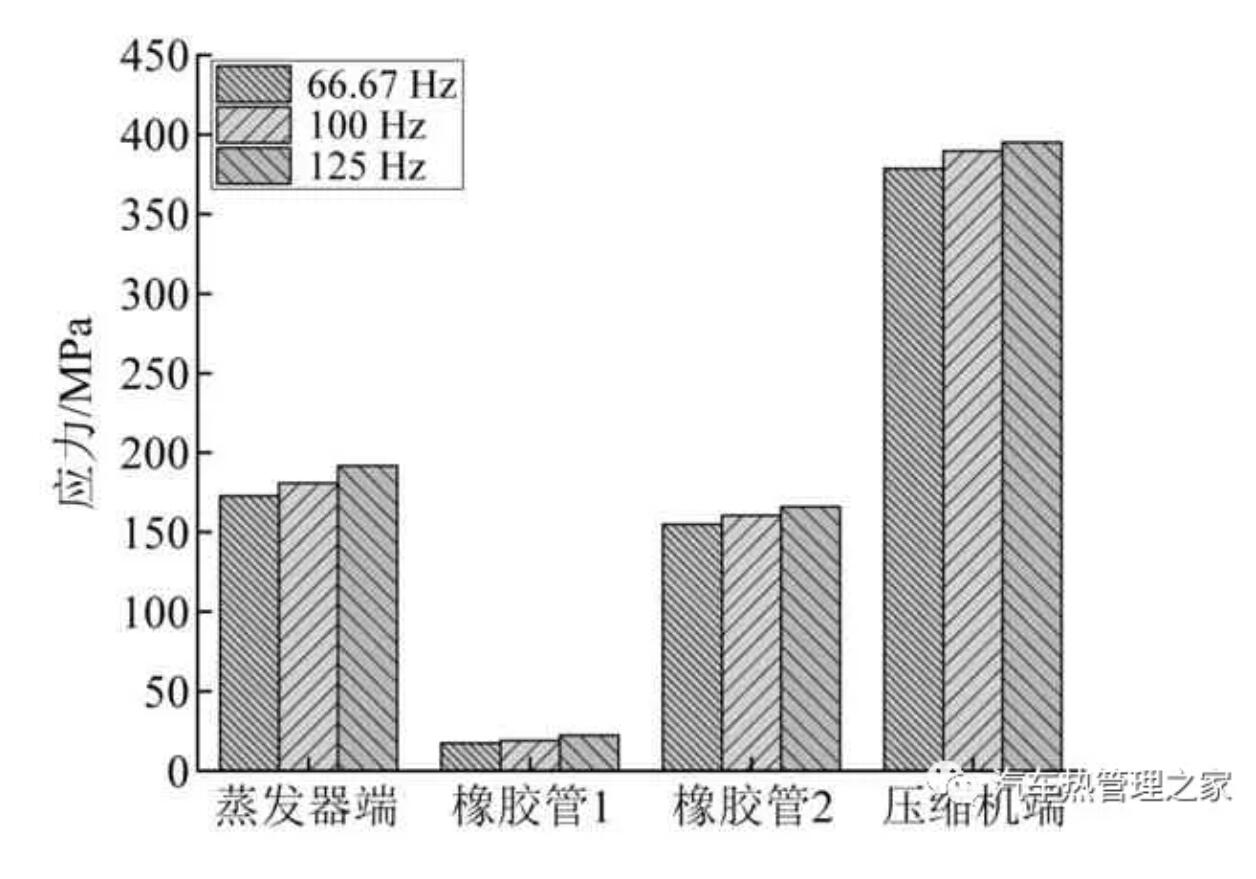
图15 不同脉动频率管路应力响应

3.4 橡胶管硬度对管路流固耦合振动的影响

橡胶管的结构布置对汽车空调管路的振动特性有着重要影响，同时橡胶管的硬度也是影响管路振动重要因素。橡胶管为多层复合结构，其硬度受中间PET编织层的材料性能影响较大，因此以PET的杨氏模量为变量，分析管路在不同橡胶管硬度下的流固耦合振动特性。

不同PET杨氏模量下橡胶管的位移振动情况，如图16所示。从图16可知，橡胶管硬度对管路的流固耦合振动特性有着重要的影响，随着PET杨氏模量的增加，管路的振动位移出现明显下降的趋势，通过改变橡胶管的硬度可以实现管路振动性能的优化。

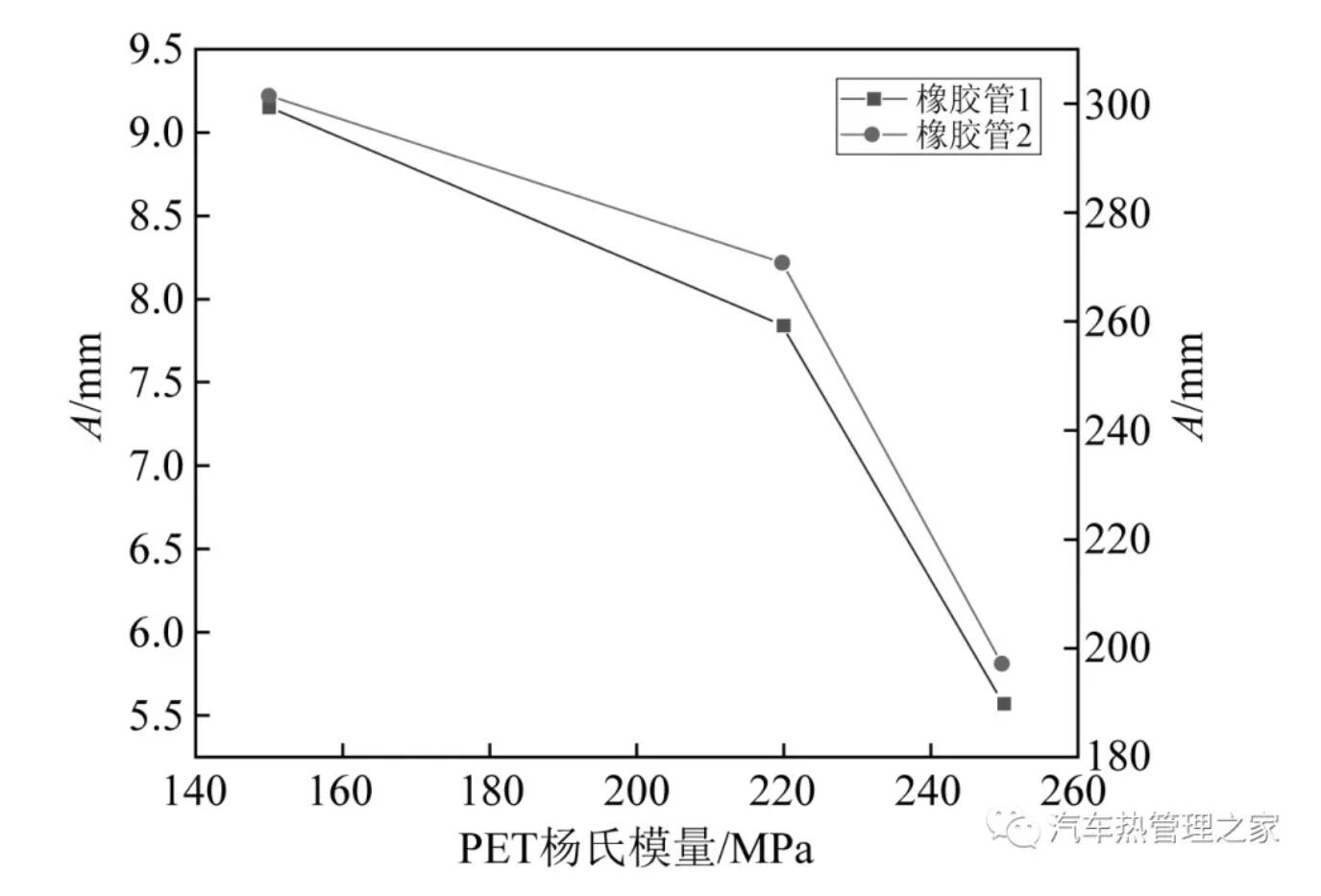
图16 橡胶管硬度对管路振动的影响

结 论

建立了某型汽车空调低压管路模型和制冷剂流体模型，采用流固耦合分析方法对管路进行振动响应分析和流场特性分析，主要结论如下：

(1)汽车空调管路表现为低频振动特点，主要振型发生在橡胶管上；在考虑流固耦合作用后，管路固有频率增加。

(2)流体压力脉动会与管路产生较强的耦合作用，特别是空调橡胶管的振动更加明显，靠近压缩机的橡胶管表现出周期性的振动，远离压缩机的橡胶管振动响应逐渐衰减。

(3)在空调管路的流固耦合分析中，不能忽略流体脉动频率的影响，流体脉动频率越高，管路应力越大，且连接压缩机的管道应力最大。

(4)橡胶管硬度对汽车空调管路流固耦合振动特性有较大影响，管路的振动位移随着橡胶管的硬度增加而减小。

本文来源：赵 勤1,2， 黄云伟1， 徐中明1， 贺岩松1， 张志飞1，1. 重庆大学 汽车工程学院，2. 重庆长安汽车股份有限公司。