寻找供应商
广告
首页 > 汽车测试技术 > 正文

悬置动刚度 - 1

2024-08-01 07:57:11·  来源：NVH老枪  
　

对于悬置动刚度的测试，传统方法是用动刚度试验机来完成。但动刚度试验机的频率范围通常只能到几百Hz，而且只能得到平动方向的动刚度，无法考虑旋转自由度。


近年来，随着电动汽车的迅猛发展，电驱悬置的设计需要更宽频的动刚度特性数据。此外，为了在研发过程中，能够更早期的预测和把控整车NVH性能，部件TPA（C-TPA）技术以及虚拟样车装配（Virtual Prototype Assembly，简称VPA）技术的应用越来越广泛，而VPA中往往还需要考虑旋转自由度。因此，动刚度试验机的局限性就越发凸显了。而近年来，基于频域子结构理论的一些新的悬置动刚度识别方法，逐渐成为了研究的热点。


1  悬置动刚度理论模型


悬置动刚度的理论模型如图1所示，2为悬置主动端，3为悬置被动端，F2为电驱作用到悬置上的载荷，F3为被动端结构（如副车架、车身）的反作用力，u2、u3分别为主被动端的振动位移。（F2、F3、u2、u3均为对应6个自由度的向量）


图片

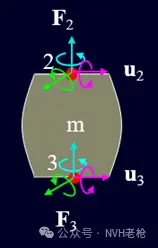
图1 悬置模型


根据动刚度的定义，有：

图片

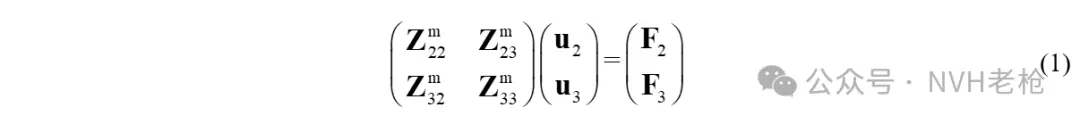
其中：Z_22是主动端原点6×6刚度矩阵；Z_33是被动端原点6×6刚度矩阵；Z_23和Z_32则是主被动端的6×6跨点刚度矩阵（根据互易性原理，二者应相等），上标m代表悬置（mount）。


F3实际上就是TPA中所说的被动端结构所承受的接触力（Contact Force）或界面力（Interface Force）。显然此时的F2和F3并不一定相等，也就是悬置主被动两侧所承受的载荷是不同的。这一点和TPA中的常规假设实际上是不一致的。例如，我们在经典TPA的悬置动刚度载荷识别中，用到的公式：


图片


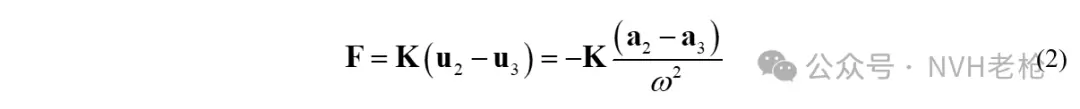
实际上是基于如下两个假设条件：


1）弹性元件质量可忽略；


2）弹性元件各自由度间不存在耦合。


满足上述两个假设条件时，公式 (1) 动刚度矩阵中的各块阵就会有如下关系：  ，此时就有了  ，即公式 (2) 。


2 子结构理论中的动刚度


子结构A、B与悬置m构成一个系统。假设在A的悬置连接2的位置，以及B的悬置连接3点位置分别作用有激励 F2A 和 F3B。


图片

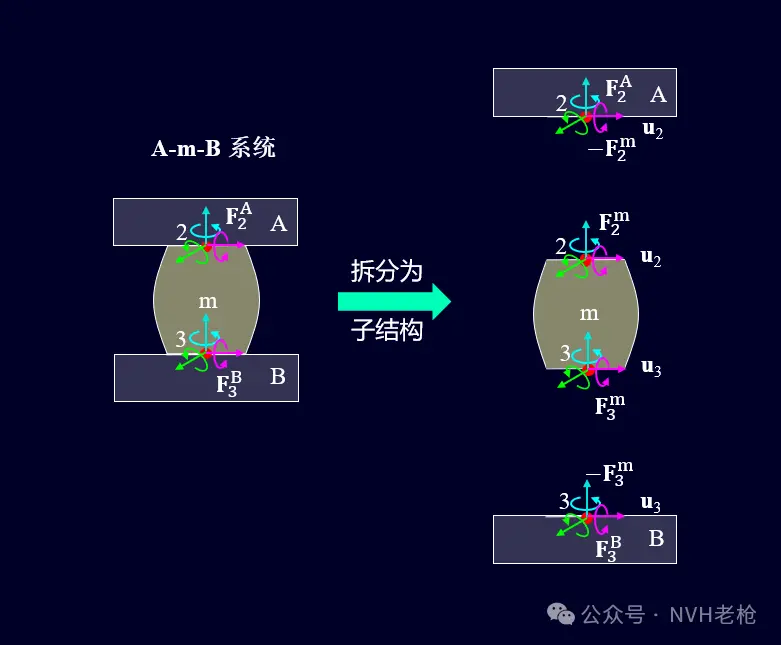
图2 A-m-B系统动刚度分析


将A-m-B系统，拆解为各个子结构，并分别进行受力分析，可得到如下方程：


图片



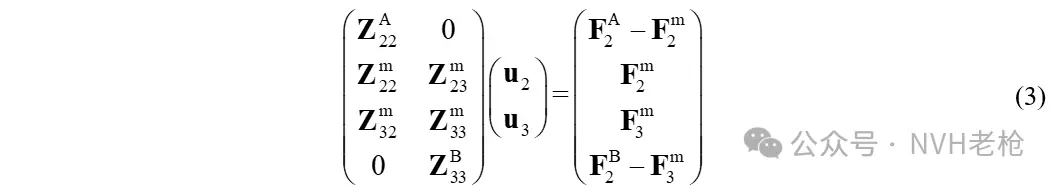
进行如下变换：等式左边刚度矩阵的前两行相加，后两行相加，对应等式右边力向量的前两行相加，后两行相加，可以得到：


图片



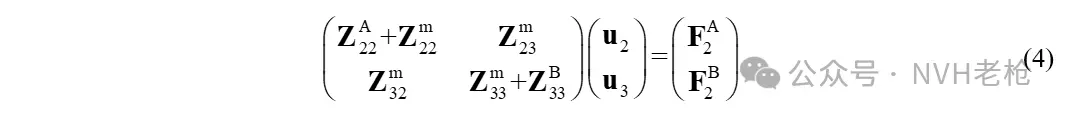
式右边对应的就是A-m-B系统的刚度矩阵 ZAmB，而这个系统动刚度矩阵是可以通过实测的系统传函矩阵 HAmB 求逆得到：



图片


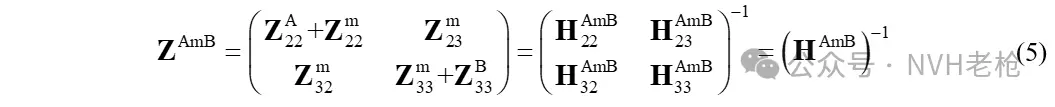
观察系统动刚度矩阵中的各块阵，可以看到非对角位置的块阵只与悬置动刚度有关，而与A、B结构无关。而这就是基于子结构理论的悬置动刚度识别方法的根本。

分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• 用户之声 | 了解HARMAN如何重塑车内音效，引领消费者新期 • 太阳光辐射实验之老化原理和自然模拟
• 车用串行总线：从特性评估到协议分析，打造测试强者之路！ • R100中规定的氢气排放测试方法（中）
• R100中规定的氢气排放测试方法（上） • 电机噪声的秘密：如何分类和解决
• 大众的疲劳强度验证及认证体系 • 联合国R100法规规定的新能源车辆动力电池的测试方法
• 基于复杂场景的结构耐久工况开发及应用 • 汽车耐久性和可靠性理论基础概述
0 条相关评论
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026620号