广告
扫频速度及扫频方向和振动响应的关系（续）
上文中，主要讨论正弦扫频振动试验中，扫频速度及扫频方向和振动响应之间的关系，并结合个人经验提供了一种比较可靠的扫频方法来寻找共振点。文中提到一个无量纲参数η和两个半经验公式，如下式（1）（2）（3）所示，式中A0为共振时振动响应完全饱和时的振幅，f0为试验体的共振频率（和本文中的fn是一个概念），本文就这三式的由来，理论上和试验上进行说明。
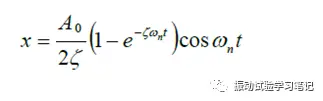
前文所述，用试验体的共振频率直接给试验体正弦定频加振（扫频速度为零），试验体的振动响应会慢慢成长，一定时间加振持续，试验体的振动响应饱和（完全共振），振幅达到Q值（Q=1/（2ζ）），如下图1所示，
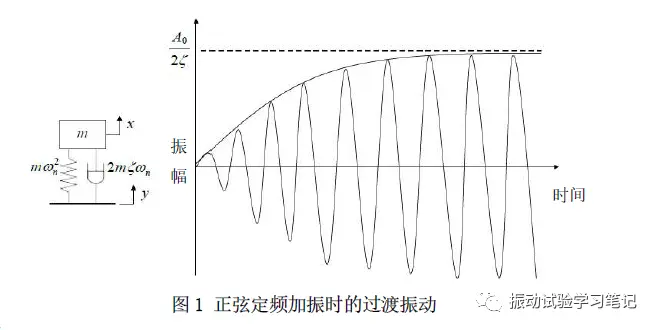
并得到，
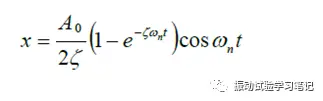
上式中可以看出，定频加振时过渡状态的振幅与ζωnt有依存关系，由试验体的Q（Q=1/（2ζ））值和负载的循环数N（N=ωnt/（2π））决定。通过以下变形可得到，
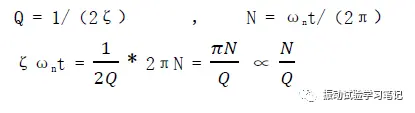
引入无量纲参数η，
正弦振动试验时的η如果可以定量评价的话，那么就能对正弦振动试验时的响应就行评价。η可以通过以下的顺序进行算出。
（1）试验体的Q值，从低量级的加振（特性确认加振）结果，利用半功率法的共振频率fn和半功率带宽Δf可以求出，如下图2，
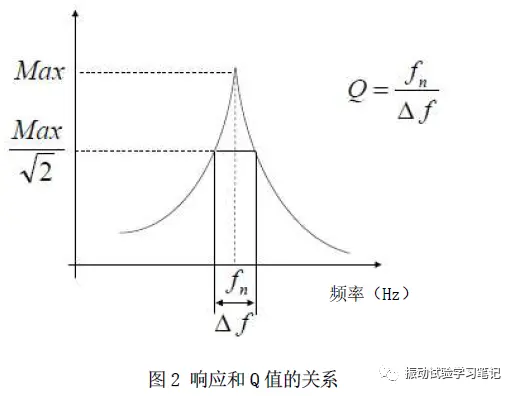
（2）正弦振动试验时的循环数是通过试验体的共振频率fn及Q值求出的半功率频带（Δf=fn/Q）内的循环数。
（3）半功率频带内的加振时间为Δt（sec），假定带宽内的扫频速度一定，则通过试验体的共振频率时的扫频速度为df，
另外，df和扫频速度β（oct/min）的关系如下，
频率和时间的函数式
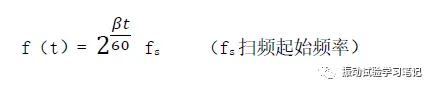
微分可得
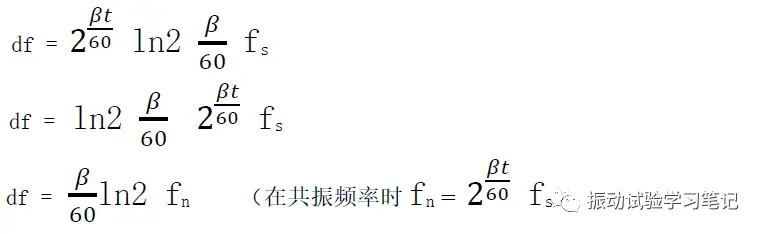
将上式代入（5）式，得到半功率频带
（4）利用试验体的共振频率fn和（6）式，可得到在Δt内的循环数N为，
最后，将（7）式代入（4）式，得到，
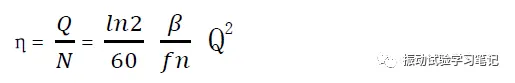
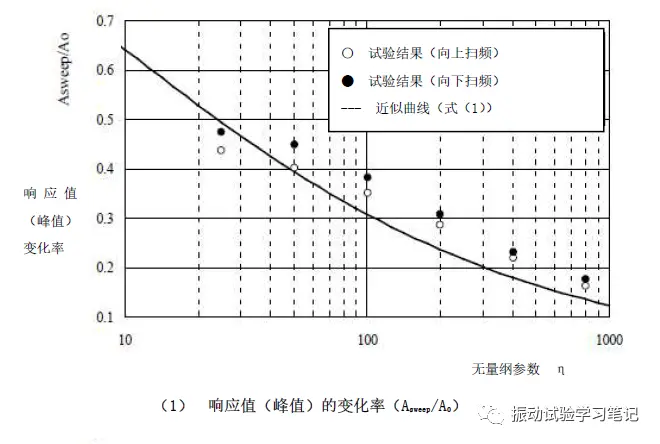
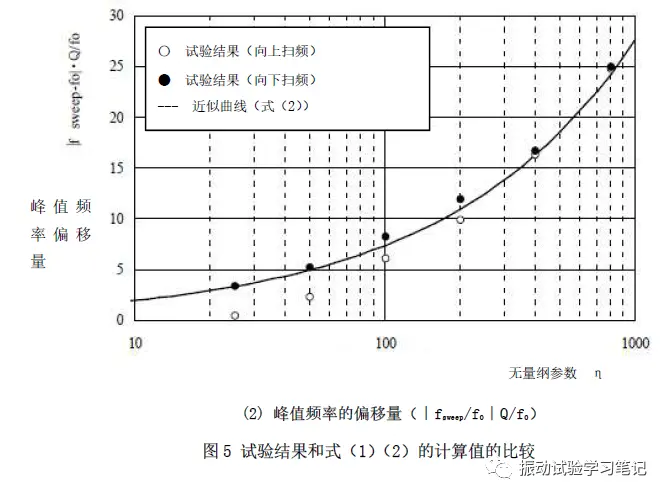
利用无量纲参数η可以对单自由度振动模型进行模拟，得到加速度响应峰值变化率及频率变化量和η的关系，如下图3所示，本模拟是将单自由度振动模型的Q值作为参数，η从0.1～1000变化得到的结果。通过模拟结果，利用最小二乘法得到近似曲线，导出半经验公式（1）和（2）。图中可以看出，峰值频率的偏移量，η越大，偏移量也越大。
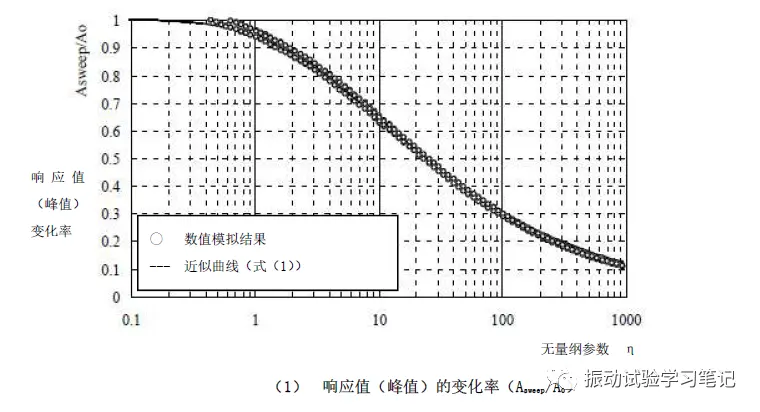
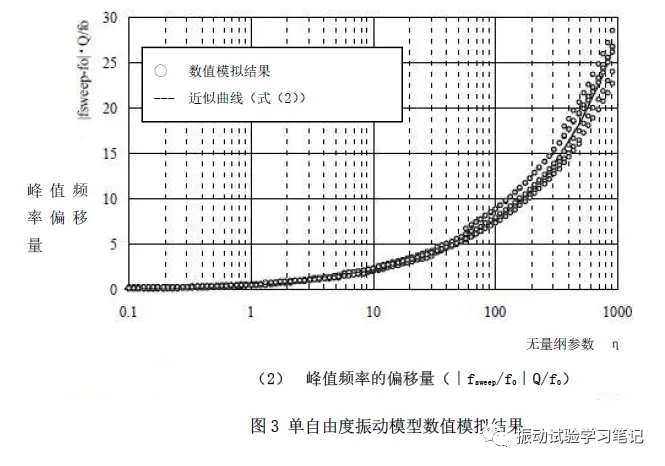
对于式（1）和（2）的精度可以通过下面的简易试验得到验证。试验体的共振频率和Q值如下表1，试验模型如图4所示。
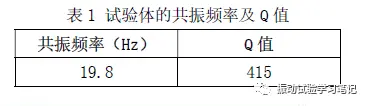
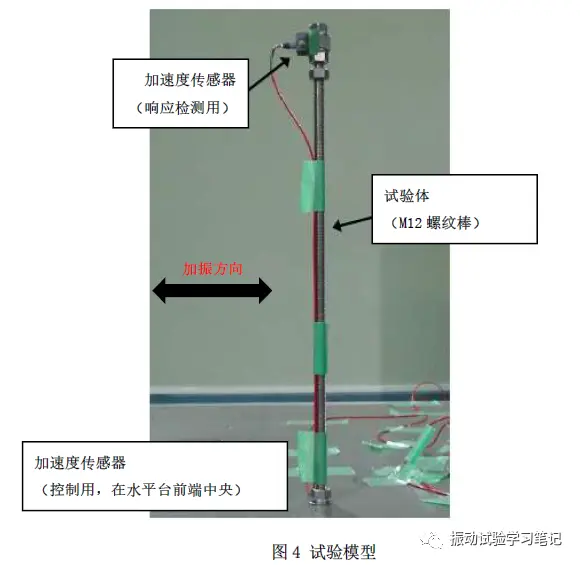
本试验，使用带有表1中动特性的试验体，进行下面6种扫频速度进行加振，
0.25, 0.5, 1, 2, 4, 8 [oct/min]
得到响应值变化率及峰值频率偏移量，扫频方向为向上扫频和向下扫频两种。试验得到的数值结果和式（1）（2）计算值曲线进行比较，如图5。可以看出，试验结果和计算值基本一致，响应值变化率最大约有0.075误差，频率偏移量最大约有2.9误差。误差可能是由试验体的动特性（共振频率、Q值）误差以及非线性造成的。
总结：
扫频速度及扫频方向和振动响应的关系，通过两篇文章来进行说明，相对来说是比较复杂，理解起来也比较吃力，供学有余力的同行者参考。如有时间和兴趣，不妨可以按照文中模型自行进行试验加以验证。
参考资料：J.A.Lollock,THE EFFECT OF SWEPT SINUSOIDAL EXCITATION ON THE RESPonSE OF A SINGLE-DEGREE-OF-FREEDOM OSCILLATOR, AIAA-2002-1230
- 下一篇：倍频程概念在扫频试验中的计算
- 上一篇：扫频速度及扫频方向和振动响应的关系
广告 
广告
广告
最新资讯
-
电动汽车电液制动系统振动和噪音优化
2024-12-25 12:09
-
汽车技术合规与海外市场准入系列：墨西哥
2024-12-25 12:00
-
1.5亿欧元投资！采埃孚西安基地扩能及研发
2024-12-25 08:35
-
车载定位标准GB/T 45086.1-2024测试技术网
2024-12-25 08:33
-
电动汽车爆胎控制系统技术解析
2024-12-25 08:22
广告
广告
