寻找供应商
广告
首页 > 汽车测试技术 > 正文

浅谈随机振动试验6 试验中若干参数说明3 自由度等参数

2024-08-05 09:14:25·  来源：振动试验学习笔记  
　

       本文主要讲述根据随机试验条件如何理解自由度（DOF, degree of freedom）等参数的概念以及一些设定的注意事项，见下图红框处。


图片

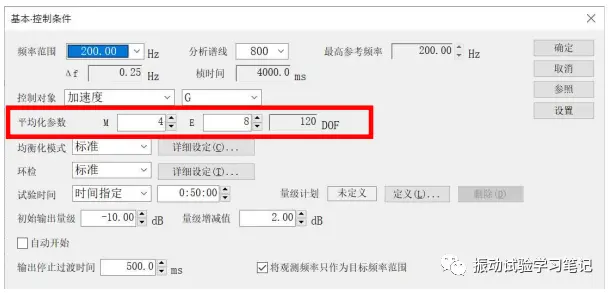
图1 随机试验参数设置界面（IMV公司K2界面）

  

 此处的自由度并非机械原理中的自由度，两者有着本质的区别。它是统计学中的一个概念，是指计算某一统计量时，取值不受限制的变量的个数，主要影响统计性参数的控制精度。在随机振动采样对总体特性参数做出估计时，由于样本的随机性，其结论总是不确定的。但是，采用数理统计中的区间估计法，这个估计值会散落在总体参数周围一定允许的误差范围（置信区间）之内，其相应的概率即为置信度，它表示区间估计的把握程度。DOF越高，得到结果的置信度越高，数据的有效性当然也越好，PSD谱的控制精度越高（当然还受振动控制仪闭环控制能力、功放动态范围等的影响，此处不再赘述。），参见下图2。

   

自由度和置信度的概念相对来说比较难以理解，但是不影响我们做随机振动试验，只要记住上面的黑字结论即可。有余力的工程师建议去看一下关于概率和数理统计的书本，还有《振动与冲击试验技术》第152-164页，以及一些关于随机振动说明的书本。

图片

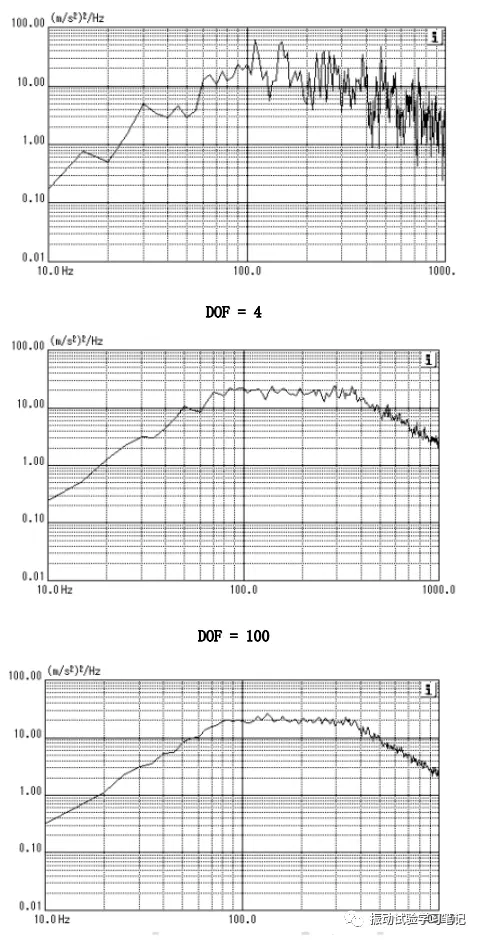
图2 自由度（DOF）和PSD谱精度关系

   

图2中，通过控制PSD响应曲线可以看出，DOF越大，控制PSD谱曲线越接近目标PSD谱，也就是控制精度越高。当然，也不是DOF越高越好，DOF越高也就意味着平均化次数越多，数据处理时间长，另外突变性数据（波形）也越难反映出来。建议随机试验设置DOF时，取100-200之间，个人一般使用120。

   

上面提到平均化的概念，那就再稍微地谈一下提高检测样本的自由度数和在控制过程中消除引入随机误差的方法，也就是图1中M和E的理解。

  

 在利用FFT方法分析随机波形的时候，1次的分析结果肯定误差很大，所以就需要多取数据，进行平均化处理。如下图3，取M帧随机波形数据，

图片

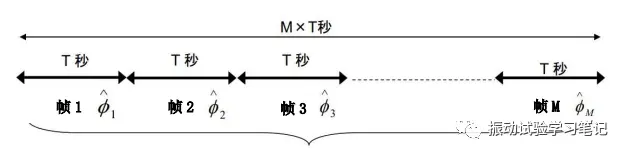
图3 算数平均法示意图


那么，M帧数据平均化后得到的控制响应谱为

图片


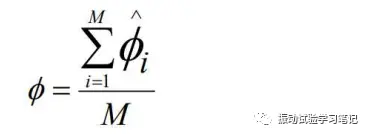
此方法为算数平均法，自由度公式K = 2M，为了使DOF为120，需要M为60，即一次控制循环需要60帧的数据，若一帧数据为1秒，就需要60秒一次来更新控制响应谱。虽然降低了功率谱的随机误差，但振动试验是一个瞬态响应的环境试验，这么长的控制循环时间，不利于振动过程的瞬时控制。

   

于是引入指数平均法，可以在短时间循环内得到较大的DOF。随机振动试验闭环控制过程中会采集到得到n个功率谱数据，其中每一个功率谱数据都包含随机振动实时状态的信息，若能将这些信息累加起来，就可以得到较大的DOF。

  

 第n回的循环，使用算数平均法得到平均值Φn，而n次的控制响应谱利用下式定义，

图片

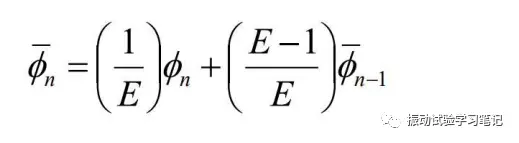
n次平均值数据Φn只使用1/E，

上一次循环的控制响应谱数据使用（E-1）/E,

也就是累积利用之前的数据，使DOF取大。

自由度的公式为

图片

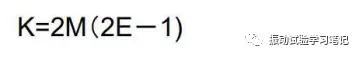
当M取4，E取8时，自由度为120，可见只要4帧数据（4秒），就可以得到自由度120，显然比第一种方法快了很多。

   

通过上述说明，是否对图1中的M和E及DOF有了一定的了解，在实际控制中并没有那么简单，为了提高自由度，还有很多算法，每个振动控制仪内部使用的原理也是有一定差别的。当然，这些处理方法，只需要了解即可对设置和操作随机振动试验有所帮助，对于一般的工程师没有必要深究下去。

   

随机振动功率谱再现是具有一定置信度水平的随机振动环境近似性模拟，需要不断地、深入地去认识它，研发出运算速度更快的随机数据处理器，也需要探讨更有效的随机数据处理算法，以便更有效地模拟产品在外部所经历的振动环境条件。


浅谈随机振动系列文章

浅谈随机振动试验1--随机有效推力和正弦推力的关系

浅谈随机振动试验2  随机振动试验4个域描述1

浅谈随机振动试验2--随机振动试验4个域描述2

浅谈随机振动试验3  频谱分析和傅里叶变换概念

浅谈随机振动试验4  PSD怎么来的？

浅谈随机振动试验5  通过PSD如何求rms值1

浅谈随机振动试验5 通过PSD如何求rms值2

浅谈随机振动试验5  通过PSD如何求rms值3

浅谈随机振动试验6  试验中若干参数说明1 均衡化处理

浅谈随机振动试验6  试验中若干参数说明2 采样频率、分析谱线等概念


参考资料：

1 《振动、冲击环境与试验》，袁宏杰、姚军等编著，北京航空航天大学出版社。

2 《振动与冲击试验技术》，胡志强 编著，中国质检出版社、中国标准出版社。

3 《力学环境试验技术》，本书编著委员会编著，西北工业大学出版社。


分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• 新能源汽车高寒环境可靠性行驶试验研究 • 充电技术揭秘 | 小小补能焦虑，拿捏！
• 探索IDIADA滑台测试设施 领略汽车安全领域创新 • ENCAP2026对自适应巡航ACC和转向辅助SA的要求（上）
• ENCAP2026对智能限速辅助ISA的要求 • 驱动电机系统与动力电池系统试验实例
• 标准研究 | 新能源越野能到什么level？快进来划重点了！ • 捷豹路虎基于R290应用于汽车热泵系统的性能实验研究
• 汽车网络安全法规(R155&R156)和标准(ISO 21434&GB 44495) • 汽车动力电池系统试验综述
0 条相关评论
  • 广告
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026917号-25