广告
浅谈随机振动试验8 非高斯型平稳随机振动试验介绍
随着可靠性试验和环境试验的要求以及计算机技术的发展，振动试验从一开始的简单正弦定频试验到正弦扫频试验，然后再发展到随机振动试验，一步步地提高着振动试验的精度。
但是，最近的随机振动试验，尤其在运输振动试验中，不仅没能再现实际负载环境条件，而且即使试验合格还会出破损事故。也就是说，对试验精度的要求越来越严格。因此，急切需要对现在的随机振动试验进行改良，提供一种更接近实际负载情况和满足高精度试验要求的试验方法。于是，非高斯型随机振动试验方法便被逐渐地提上了应用的日程，随着技术的发展，现如今较好的振动控制仪基本上都能对应此种试验方法。
先来谈谈现在应用最广的随机振动试验（高斯型），是一种含有各种频率波形成份的不规则振动。通过设定试验条件的加速度密度谱（PSD），然后通过振动控制仪按照此PSD产生随机波形进行振动。如下图1便是一般的运输试验规格PSD曲线（JIS Z 0232）。
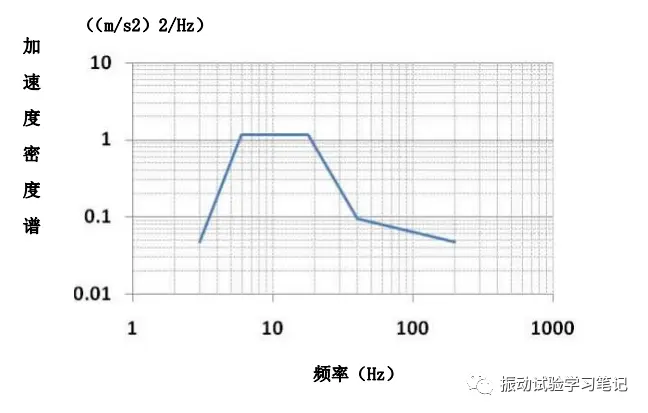
图1 加速度密度谱示例
随机振动试验，加速度的概率密度函数分布为正态分布（高斯分布，高斯型命名的来源），一般用下式表示，
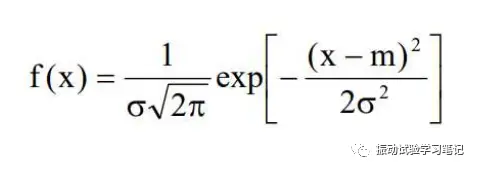
式中，x为加速度，m为加速度的平均值，f（x）为概率密度分布，σ为标准偏差。图2为其概率密度分布曲线，图中可以看出随机振动试验的加速度符合高斯分布，超过3σ的大加速度出现的概率极低，仅有0.3%。
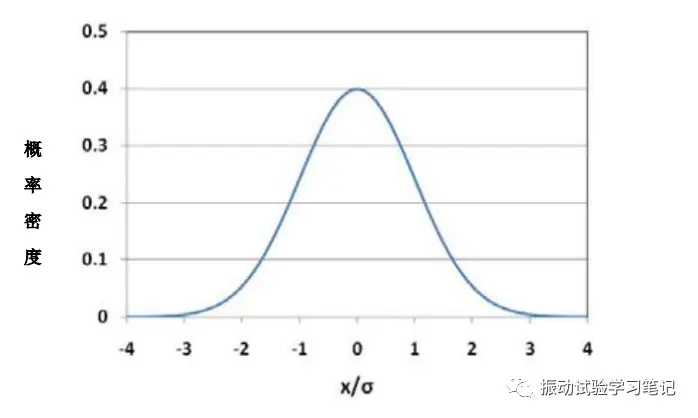
图2 高斯分布
接着再来看实际情况下发生的振动，以运输试验为例。在实际运输中，由于路面凹凸等的影响，加速度不满足高斯分布的情况很多。比如图3显示的是某货车架上的振动波形，图4是其振动加速度的概率分布情况。图4中可以看出实际分布不满足高斯分布，超过3σ的大加速度出现的概率有1.5%，相当于高斯分布的5倍。
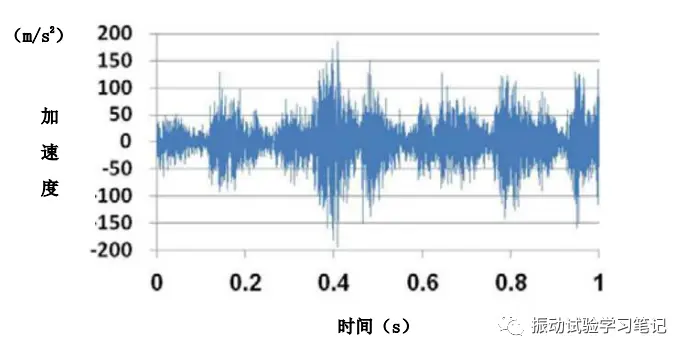
图3 某货车架实际振动波形
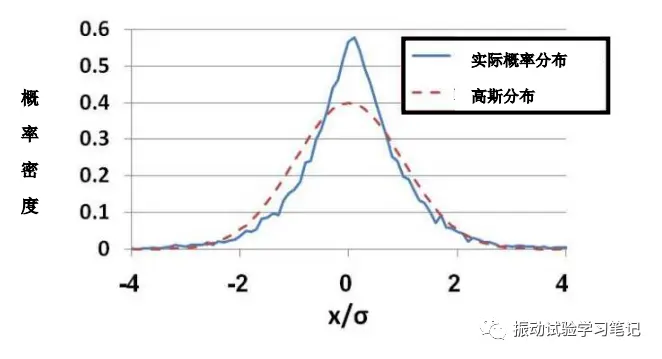
图4 波形（图3）对应的概率密度曲线
第三，如何来定量非高斯型振动试验。还是以上面实际运输时的振动为例，发现货车架上实际的加速度分布不是高斯分布的场合比较多。通过学者的研究，提出了偏度S（Skewness）和峭度K（Kurtosis）两个概念来定量化非高斯型随机振动试验，定义式子如下，概率论学的好的，是不是感觉和概率论里面的3阶中心距和四阶中心矩的概念差不多？
式中，x为加速度，m为加速度平均值，N为数据点数，σ为标准偏差。
来看看偏度的含义。高斯型平稳随机振动的概率密度函数曲线是相对于均值m对称分布的，其偏度S为零。若平稳随机振动时间历程x（t）的偏度S不为零，则表明概率密度函数曲线关于m不对称。当S大于零的场合，概率密度函数曲线的峰值偏左，如图5（a），；当S小于零的场合，曲线的峰值偏右，如图5（b），其峰值对应于平均值m。
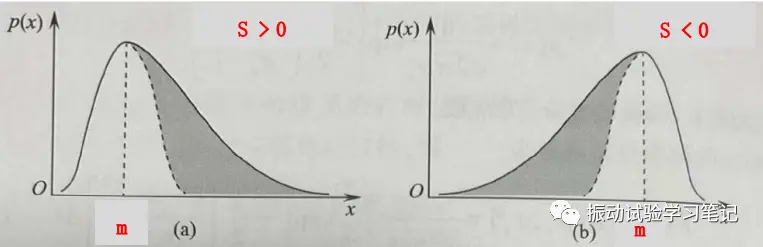
图5 偏度示意图
再来看看峭度的含义。峭度的取值范围为1～∞。高斯型平稳随机振动的峭度K等于3。与具有相同均值和均方值的高斯随机振动相比，当K小于3时，非高斯型的概率密度曲线的峰值较低，整个峰较宽，但尾部的量值较低；对于均匀分布信号，K为1.8。当K大于3时，非高斯型的概率密度曲线的峰值较高，整个峰较窄，但尾部的量值较高，极大值出现的概率较大，具体如图6所示。
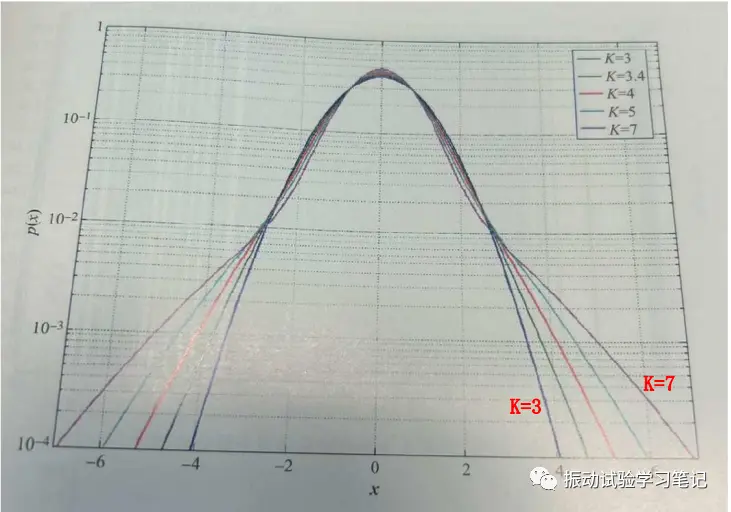
图6 不同峭度的概率密度函数曲线（平均值为零，方差为1）
有了上面的概念，实际中的波形和概率密度曲线又是什么样的呢？看图7，高斯型随机平稳振动，即现今最普及的随机振动试验，K=3，S=0。
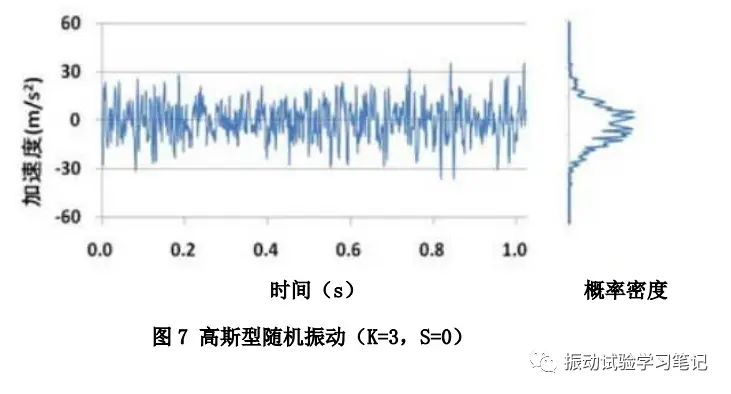
图8中，K值偏大（远大于3），就会出现较多的极大值。
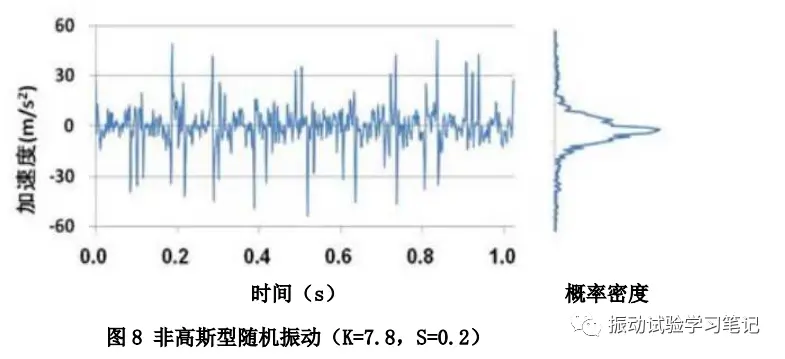
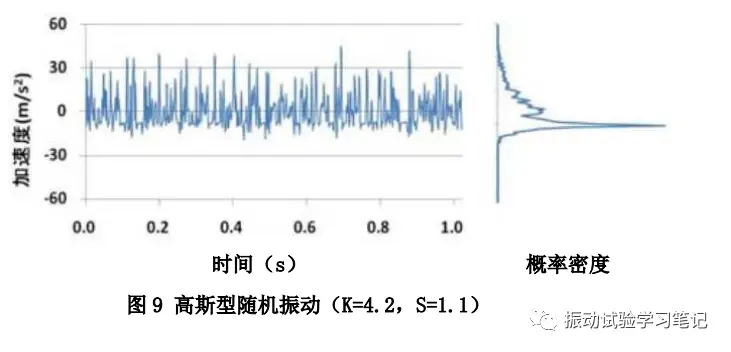
图9中，S值偏大（远大于零），加速度会向正方向偏移分布较多。当然，如果S远小于零，加速度会向负方向偏移分布较多。
结束语：
通过以上的介绍，相信会对非高斯型随机振动试验有一定的认识。进入21世纪后，针对偏度和峭度的量化算法，通过计算机硬件产生非高斯型振动波形的研究如火如荼，并取得了很可喜的成果，已经开始在振动试验中得到了应用。有资源的工程师，建议自己编辑一下试验条件，运行一下非高斯型随机振动试验，尤其是通过耳朵可以比较一下两者之间的运行声音区别。
非高斯随机振动试验已在运输试验中得到广泛应用。目前，其在产品的疲劳评价试验中尚未推广开来，很多学者对于里面的评价方法等细节还在研究中，一旦得到广泛应用，相信对振动试验的精度产生飞跃性的影响，让我们拭目以待。
本文内容大部分来自日文原稿：
1 面向振动试验精度向上的技术课题—随机振动从高斯型向非高斯型，细山 亮、中岛 隆胜，2009年3月31日
参考资料：
1 《振动环境试验》，国防工业出版社，王帅、夏益霖、荣克林 著，P21非高斯平稳随机振动。
广告
广告
最新资讯
-
直播｜中国汽研：重型车温室气体企业平均方
2024-11-23 17:42
-
美国FCC正式划定5.9GHz频段用于C-V2X技术
2024-11-23 17:41
-
标准立项 | 《自主代客泊车 预期功能安全测
2024-11-23 16:13
-
长三角（盐城）智能网联汽车试验场气象多级
2024-11-23 16:11
-
CSAE汽车可靠性技术分会第二届委员会第二次
2024-11-23 16:09
广告
广告
