广告
振动试验入门-振动试验装置基础知识4
随机试验
1 随机试验的目的
正弦试验比较传统，相对来说比较简单容易理解，随机试验就比较复杂且难理解。实际现场产品受到的振动基本上都是随机波或者冲击波，所以随机振动试验更接近产品受到的真实振动状况。
由于以前技术上的问题，只好来正弦试验来进行代替，实际加振的并不是现场受到的真实振动。后来技术的发展，随机试验变为可能，但随机振动控制仪的价格太过昂贵，仅在防卫、航天航空方面得到应用。最近，数字技术的发展，随机振动控制仪的价格相对下降，使更接近真实振动状况的随机试验或冲击试验得到普及。
2 随机波和正弦波的比较
一般试验体构造上由含有各种各样共振模式（各种频率不同地方的共振）的零部件构成，正弦波加振只能激励起试验体的共振频率或共振频率整数倍的频率。而随机波本身就含有各种频率成分，能同时刻激励起试验体上全部的共振成分，更接近实际现场的振动环境。
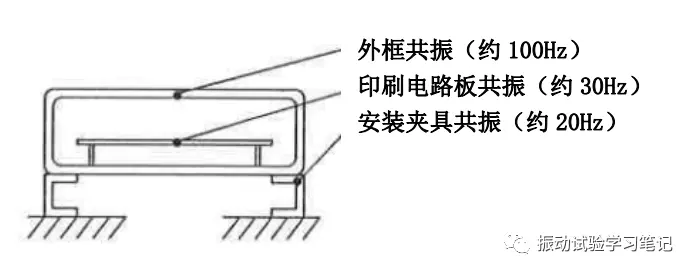
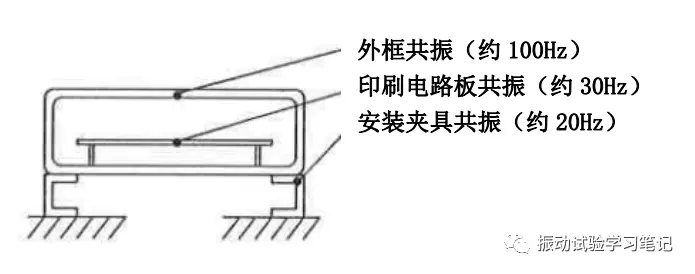
以试验体汽车音响为例，正弦波加振只能激励起音响整体的共振频率，但随机波加振，可以同时激励起所有组合部件的共振。
另外，通过正弦波和随机波在时间轴上的波形，可以看到振幅分布密度（各个振幅出现的概率密度，随机波符合高斯分布）曲线。
上图中，正弦波在最大加速度（加振力最大处）处出现的机会最多，随机波在零值处（加速度为零处）出现的机会最多，换句话来说，正弦波试验其实比真实的现场振动（随机波或冲击波）来得苛刻（过试验）。一般随机试验，振动量级用加速度有效值（rms值）来衡量表示。
3 功率谱密度（PSD）
随机振动试验条件通过功率谱密度（PSD）来表示，1Hz宽度对应能量的平均值，单位[（m/s2）2/Hz],或者使用[m2/s3]、[g2/Hz]。加速度的有效值如下图所示，斜线面积开根号计算。
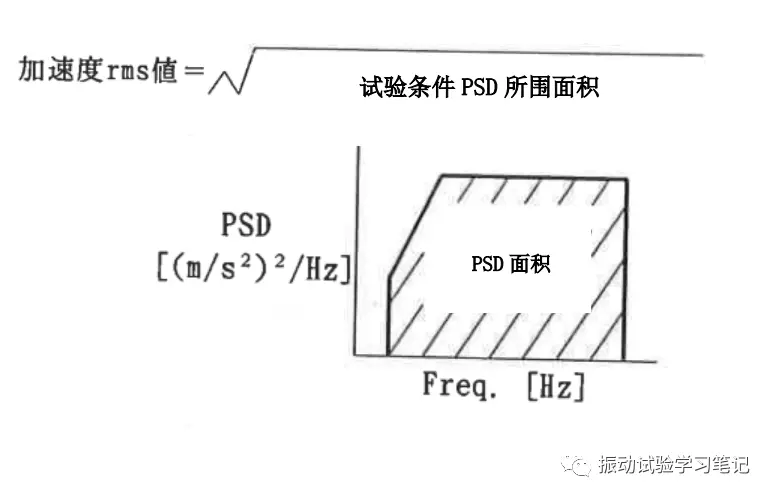
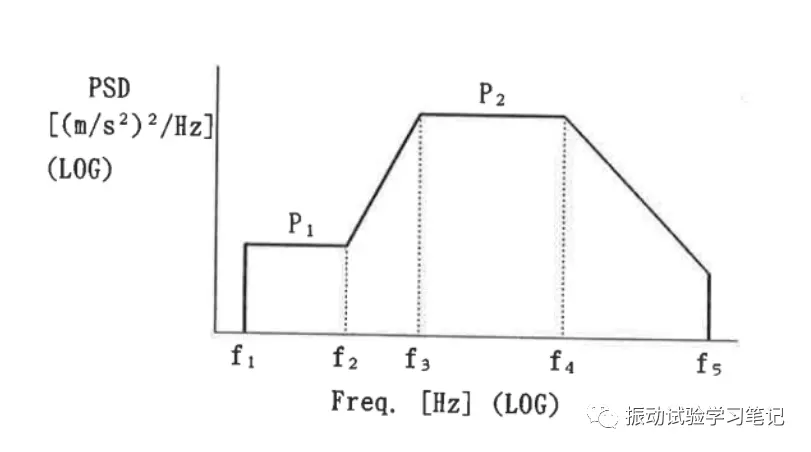
上图求加速度有效值的话，需要计算PSD曲线所围的面积，由于是在对数坐标下的曲线，在直线坐标下这些直线或斜线都是指数曲线，计算起来比较复杂，具体计算可参考以前的文章《浅谈随机振动》中的介绍，此处不再赘述。通常计算加速度有效值，建议使用随机振动控制软件，既简单又快速。
4 随机振动试验的加振力
随机试验所需加振力的计算和正弦振动试验的计算相似，即
试验实施时，使用3项计算出来的加速度rms值计算加振力。但是需要注意的是，随机加振力受试验条件PSD、试验体质量和形状等的影响，一般需要满足下面的条件。
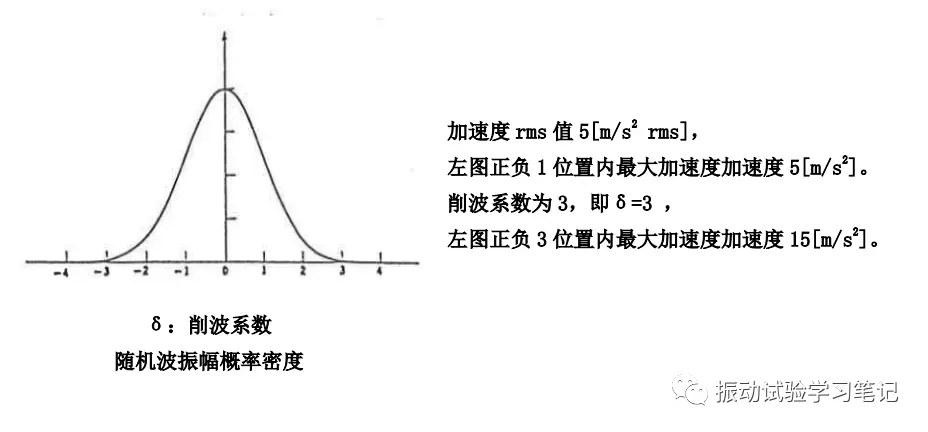
5 高斯分布（正态分布）
随机振动的振幅（位移、速度、加速度）概率密度满足高斯分布，大振幅振动发生的概率很低，但不代表不发生，发生的话就会超过振动试验机的额定式样值。为了防止这种现象发生，就需要使用削波系数（δ=3）来加以控制，即最大振幅控制在rms值的三倍以下，但也只能控制99.73%的振幅，但可以认为试验没有问题。
冲击试验
1 冲击试验的目的
如前所述，实际环境下的振动大部分是随机波及冲击波。冲击波也和随机波一样，含有很宽的频率成份，可以同时激励试验体的共振成份。随机波情况下，振动波形符合高斯分布，接近真实环境。冲击波形的话，短时间内加振特殊波形，能够再现试验体的特殊问题故障。例如，搬送物品中的冲击、爆破冲击等。
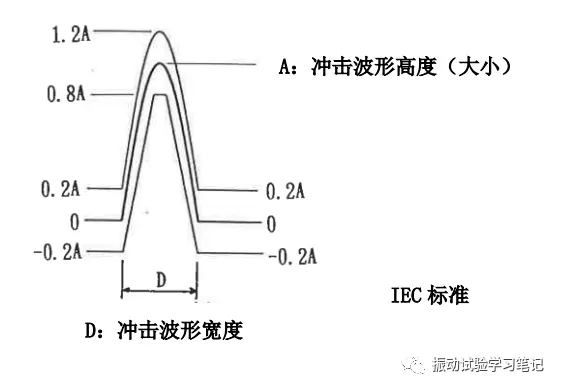
2 典型冲击波形
一般的冲击波形有半正弦波、锯齿波、三角波、矩形波等，下面就半正弦波进行说明。目标波形如下图，按照规格标准（IEC、GB、MIL等）允许容差也不同，试验实施时，响应波形在容差范围内即可，必要的时候（试验体较大等情况），只考虑波形在上升沿容差内也可以认为没有问题。
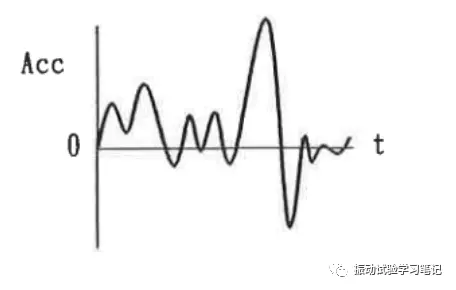
3 实测波形再现
典型冲击波形不能再现实际现场故障的情况下，可以通过加振实测波形来进行振动冲击试验。对实测波形进行规格化处理相对来说比较难，无法规定波形高度和宽度，但可以明确波形，属于特殊处理方式，具体如何评价还需要特例分析。
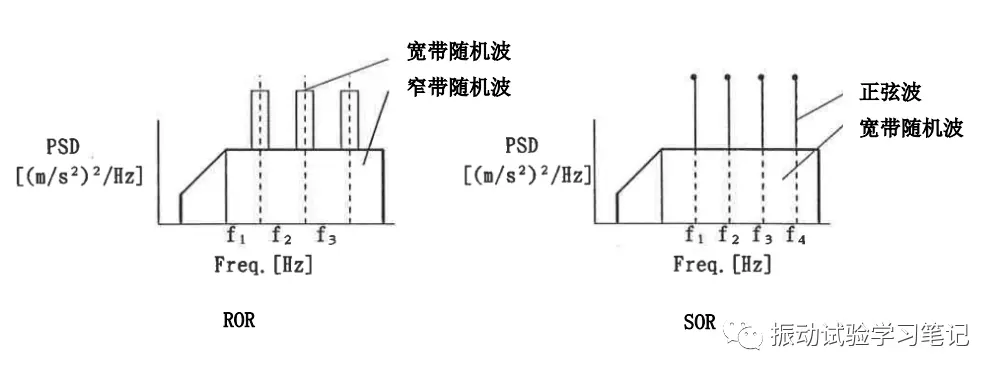
ROR/SOR试验
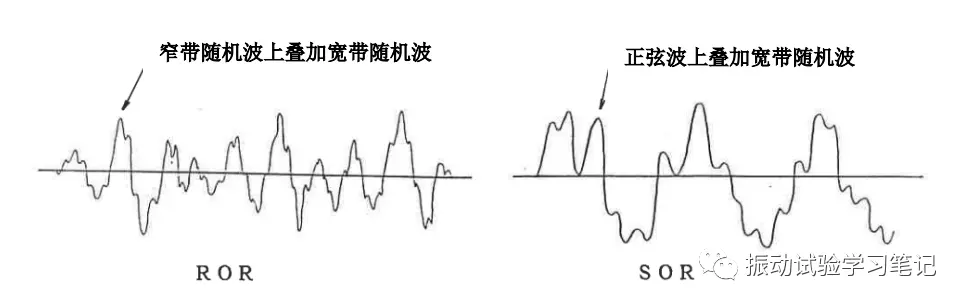
ROR：random on random，是宽带随机波形和窄带随机波形的叠加。
SOR：sine on random，是宽带随机波形和正弦波形的叠加。
这些试验主要适用于安装在引擎等回转体附近的试验体振动试验，回转体较近的用SOR，离回转体比较远的用ROR。
【例】
ROR
宽带随机波形上有数个窄带随机波，窄带随机波可以扫频实现。
SOR
宽带随机波形上数个正弦波，正弦波也可以扫频实现。
小结：
到此为止，振动试验装置基础知识基本上说明完毕，入门级的知识，很多内容都是泛泛而谈，主要目的是使入门者有个大致的理解。下一章将对加振机导入内容以及做试验中一些注意事项进行说明。
广告
广告
最新资讯
-
直播｜中国汽研：重型车温室气体企业平均方
2024-11-23 17:42
-
美国FCC正式划定5.9GHz频段用于C-V2X技术
2024-11-23 17:41
-
标准立项 | 《自主代客泊车 预期功能安全测
2024-11-23 16:13
-
长三角（盐城）智能网联汽车试验场气象多级
2024-11-23 16:11
-
CSAE汽车可靠性技术分会第二届委员会第二次
2024-11-23 16:09
广告
广告
