广告
振动试验入门 其他相关事项8 振动控制仪的控制原理
振动试验机的控制仪（振动控制仪）主要由数字分析（频率分析）部分、数字伺服部分构成，如下图1所示。数字分析部分执行频率分析（正弦波振动的频率响应分析、随机波振动的PSD分析），数字伺服部分则根据频率分析结果和控制目标的量级差生成驱动信号。
频率分析比较复杂，试验相关人员不需要详细了解，知道有这么一回事即可。本文就数字伺服部分实施的一般控制原理进行说明。
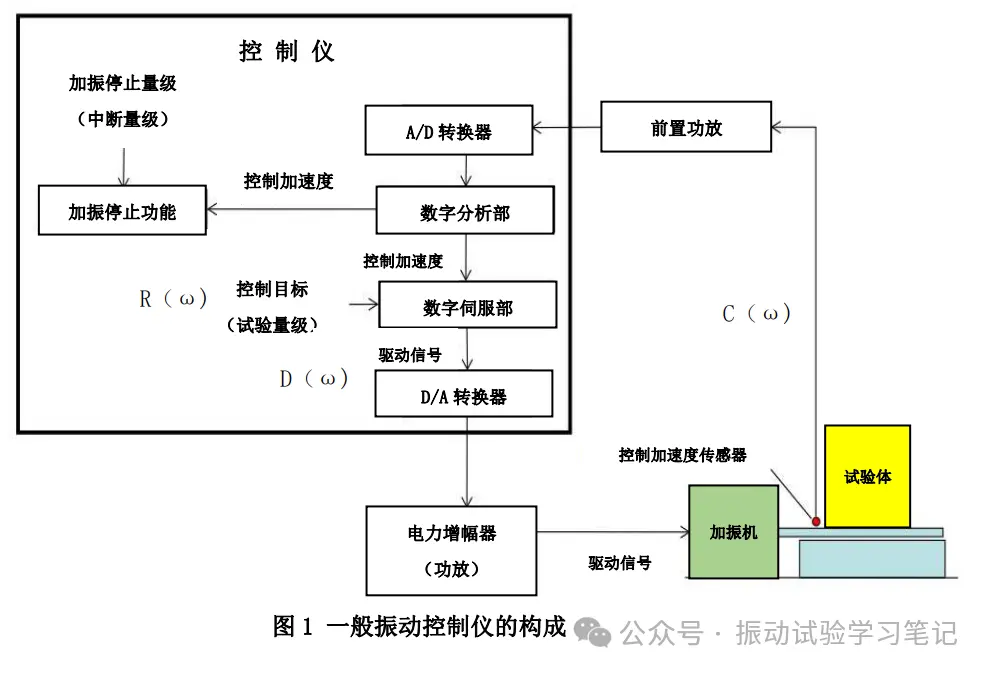
图1中，数字伺服部分生成的驱动信号D(ω)，通过电力增幅器放大，驱动加振机。通过计算加振系的传递函数Z(ω)，驱动信号D(ω)使控制点加速度量级C(ω)和控制目标R(ω)一致。传递函数Z(ω)即驱动信号D(ω)和控制点加速度量级C(ω)的比【Z(ω)=D(ω)/C(ω)】，通常，加振实施前使用低量级的随机加振，振动控制仪自动取得。加振系线性场合，为了控制点的加速度C(ω)和目标值R(ω)一致，驱动信号D(ω)可通过下式求出，
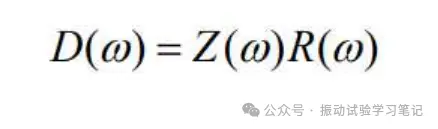
加振系非线性场合，实际加振时控制仪的传递函数Z(ω)是变化的，驱动信号会根据控制点加速度量级C(ω)和控制目标R(ω)而产生差值。为了补偿这个差值，需要逐次分析控制点的加速度量级，为了接近控制目标需要不断的修正驱动信号。驱动信号的修正量ΔD(ω)可通过下式计算，
这个修正量ΔD(ω)跟控制点加速度量级和控制目标R(ω)的差ΔR(ω)成线性关系，线性系数即加振系的传递函数Z(ω)。所以，传递函数Z(ω)是控制中最重要的一个参数，修正次数少的情况下更接近控制点的加速度目标值，就需要取得高精度的传递函数Z(ω)。
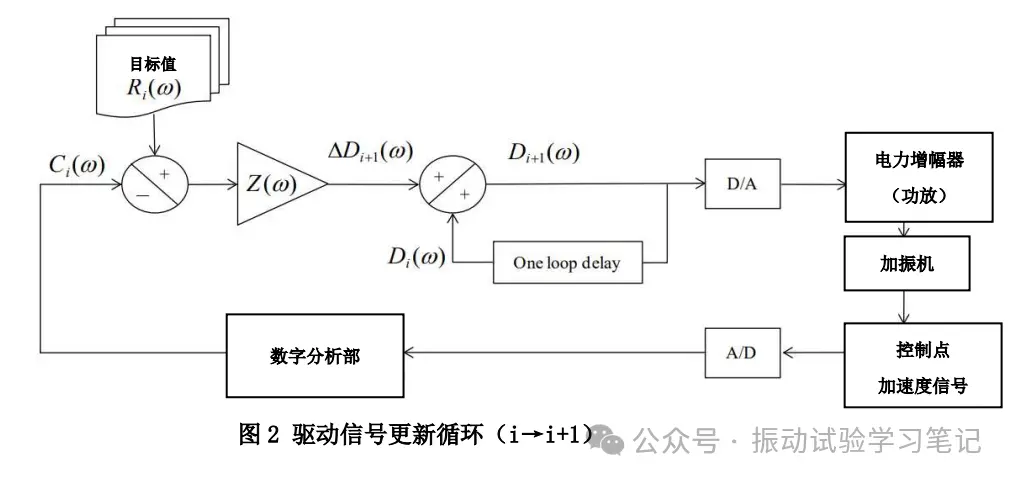
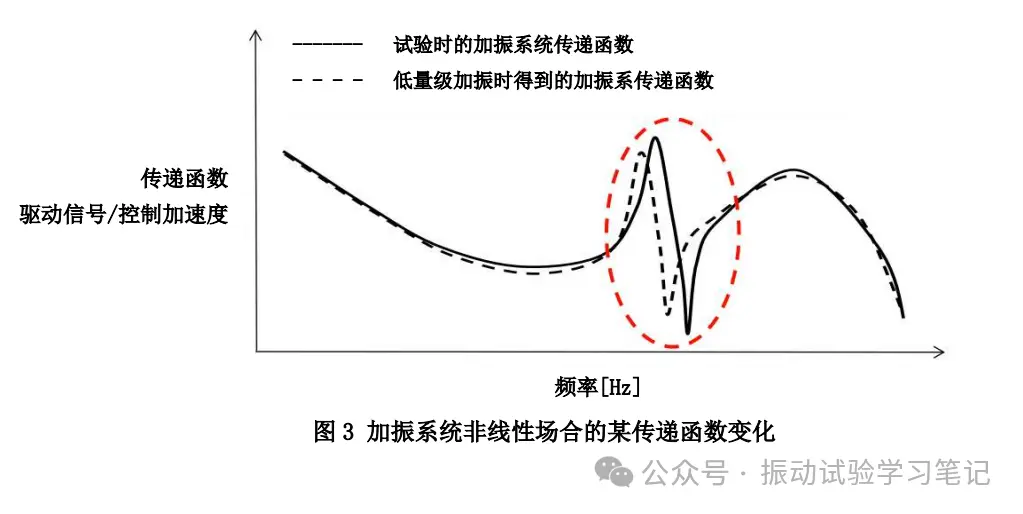
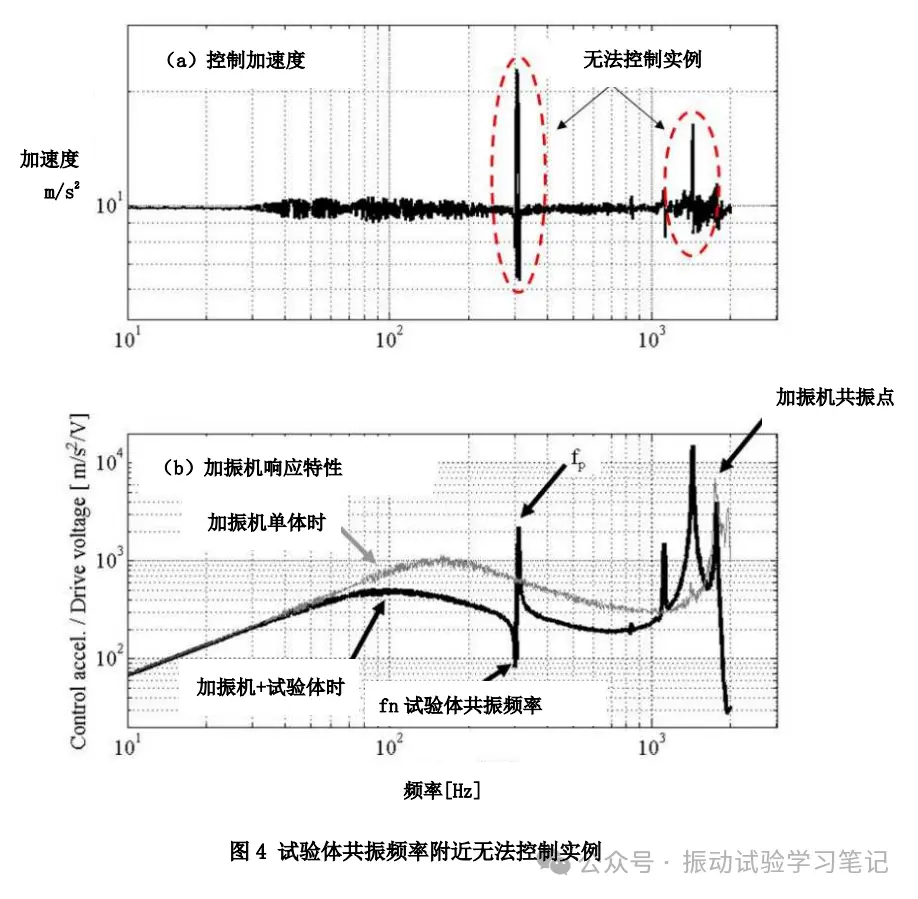
传递函数Z(ω)在试验体的共振频率附近会产生大的高峰值和低谷值，非线性的原因是传递函数的变化率在共振频率附近比较大，如图3，驱动信号的修正量也跟着变大，从而导致控制的跟踪性不足，控制结果和目标值无法一致，产生大的差异。此现象在随机振动时加振量级上升时（比如-6dB→-3dB→0dB）以及非定值加振正弦振动时容易出现。图4是300Hz附近有共振频率的试验体正弦波振动的控制结果。试验体共振频率附近，控制系统的追踪性不足，导致一时的控制过冲（overshoot）发生。
针对上述加振系统的非线性需要改善控制的跟踪性不足，使各驱动信号更新循环时的传递函数Z(ω)变化尽可能的小。随机波加振量级上升时，可以将上升量的刻度尽量细分变小，从而相对性的减小传递函数Z(ω)的变化。正弦波加振时，同样可以使用针对阶段式加大量级逐次修正传递函数的设备，即细分上升刻度达到改善。无上述设备的时候，也可以通过设定较慢的扫频速度，即单位时间内驱动信号修正量变小来改善控制的跟踪性。但是，需要注意的是，此方法会导致试验体上的振动负荷循环数增加。
本文主要简单说明振动控制仪内部的控制原理，即为了使控制加速度和目标加速度一致，通过改变驱动信号得到，驱动信号的变化需要根据带有试验体加振系统的传递函数进行。由于试验体共振频率（共振点）的影响，导致传递函数变化大，驱动信号无法跟踪变化的情况下会导致控制过冲发生。最后，介绍两种可解决过冲问题的方法。
此文对从事多年振动试验的人员会有一定的帮助，对于初入者比较难理解，建议理解传递函数的概念即可。
广告
广告
最新资讯
-
NVIDIA 发布 2025 财年第三季度财务报告
2024-11-21 13:30
-
Mack卡车为买家推出创新的虚拟现场探索体验
2024-11-21 13:29
-
氢燃料电池卡车从1到100要多长时间？戴姆勒
2024-11-21 13:28
-
聚焦消费者用车极限环境，2024中国汽研汽车
2024-11-21 13:21
-
新能源汽车高寒环境可靠性行驶试验研究
2024-11-21 13:19
广告
广告
