广告
利用线性结构对高度非线性的车辆动力学进行精确控制
曲线坐标系定义了车辆相对于所需参考路径的位置，如图 3 所示。横向误差是从路径上最近的点到车辆质心的距离。为沿路径的距离和是车辆航向与最近点处路径切线之间的角度。漂移时，始终为非零，因为车辆不再指向其行驶的相同方向。在平衡时，航向误差与侧滑角相反（为负的侧滑角）。路径跟踪动力学由以下公式描述。
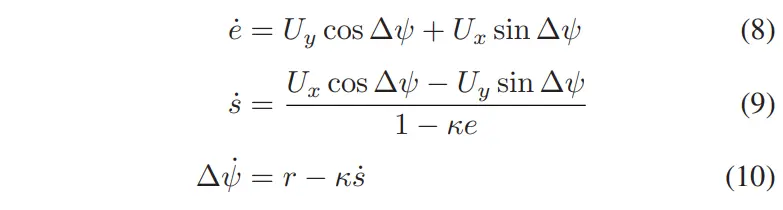
请注意单轨模型方程、Fiala 轮胎模型和路径跟踪模型中的非线性。虽然这个方程组很好地代表了车辆动力学，但它不允许直接应用线性控制技术。
Ⅲ 动力学线性化
正如 Bárdos 等人所表明的，线性化漂移平衡的动力学会导致模型具有足够的精度来成功控制，并且足够简单地用于线性控制技术 [12]。这里介绍的研究更深入地研究了线性化动力学。在本节中，我们解释了线性化方法，在仿真中演示了为什么关于漂移平衡的线性化是有效的，并研究了各种漂移平衡的特征向量，以进一步了解漂移平衡附近的动力学行为。
A. 线性化方法
平衡状态由状态和输入的组合定义，其中状态导数为零。求解零态导数（1）–（3）可以得到由六个值定义的平衡： 。用于表示论文其余部分的平衡值。
线性化方法对状态方程中涉及车辆动力学的项和与路径跟踪有关的项采用不同的方法。我们选择使用泰勒级数展开对车辆动力学方程进行数值线性化。虽然运动方程 (1)、(2) 和 (3) 可以通过分析线性化，如 Hindiyeh 在文献 [11] 中所示，但这需要额外的假设条件。由于本文的目标之一是研究原始方程和线性化方程在平衡点上的相似性，因此引入额外假设的弊大于闭式表达的利。相比之下，路径方程(8) 和 (10) 的分析线性化不需要在和常量之外做其他假设。因此，分析线性化可以应用于路径方程，在不影响精度的情况下提供更多洞察力。
状态方程的解析偏导数和相对于状态向量如下所示：
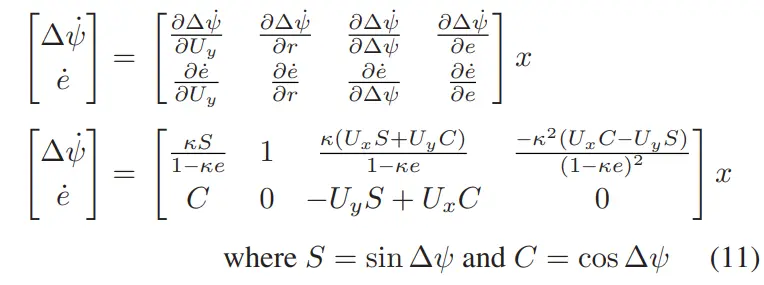
在计算解析偏导数后，在状态的平衡值处计算部分导数以产生（12）。注意。
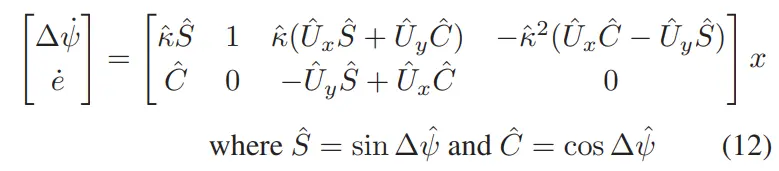
在纵向速度恒定的假设下，则完全线性化模型为：
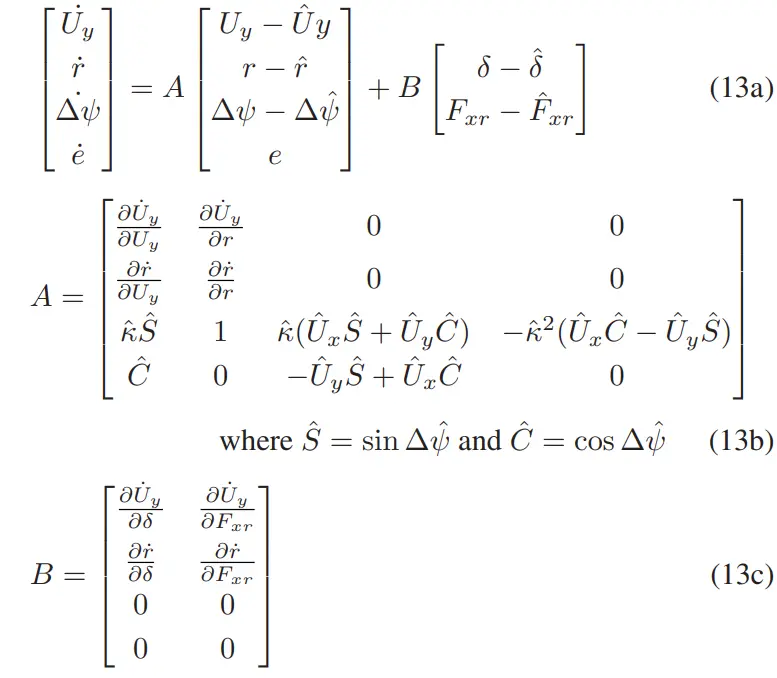
在这组状态方程中，转向角和后轮纵力，包括可用于控制器设计的输入。接下来的实验使用前制动器在单独的控制回路中强制执行恒定速度的假设。为简单起见，数值线性化没有考虑前制动器对轮胎前侧向力的影响，因为在漂移平衡中，前侧向力通常低于其峰值 [11]。实验结果更详细地讨论了这种选择的影响。
广告
广告
编辑推荐
最新资讯
-
纯电动商用车制动抖动问题解决方案
2024-11-22 07:54
-
NVIDIA 发布 2025 财年第三季度财务报告
2024-11-21 13:30
-
Mack卡车为买家推出创新的虚拟现场探索体验
2024-11-21 13:29
-
氢燃料电池卡车从1到100要多长时间？戴姆勒
2024-11-21 13:28
-
聚焦消费者用车极限环境，2024中国汽研汽车
2024-11-21 13:21
广告
广告
