广告
利用线性结构对高度非线性的车辆动力学进行精确控制
图 10.状态跟踪性能，用于跟踪单个平衡。蓝色线表示测量值，黑色虚线表示平衡值。在这个实验中，右后轮胎分层。
C. 准平衡轨迹
1） 扩展控制器以跟踪准均衡轨迹
为了证明这种线性化方法在多个工作点上有效，我们采用该控制器来跟踪准平衡轨迹。最初在 [15] 中描述并在 [5] 中进一步发展，准平衡轨迹上的每个点都是一个平衡。图 5 显示，附近漂移平衡之间的动力学变化平滑，表明线性控制适用于此类轨迹。
我们使用第 IV 部分的控制器来跟踪准平衡轨迹，方法是沿参考轨迹每 0.25 m 线性化，并根据车辆的进度更新使用的线性化。整个准平衡轨迹使用与跟踪单一平衡时相同的和矩阵以及值。通过改变线性化点，控制器变成了增益调度控制器。在轨迹上的每个点，我们都会更新线性化并计算新的反馈增益，但控制器结构在其他方面保持不变。
2） 准均衡结果
图 11 显示了在这个准平衡实验中跟踪的路径。该路径的半径称为“盒式磁带”，在 7 到 12 m 之间变化，同时保持平衡参考状态。
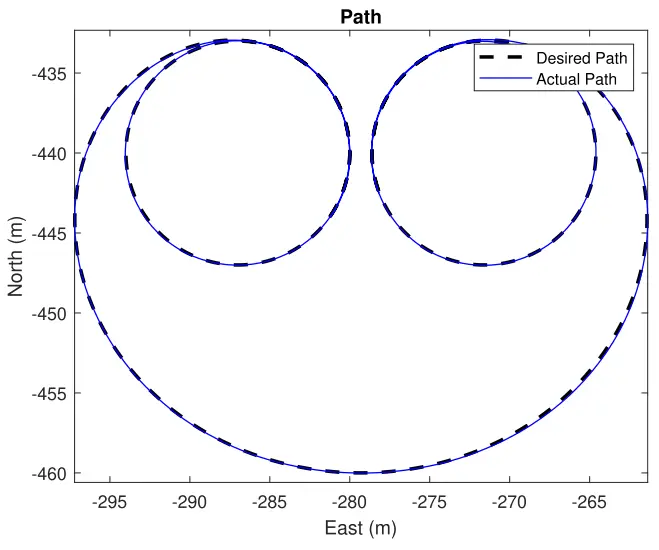
图 11.准平衡轨迹期间车辆所需路径和实际路径的俯视图。
我们将实验结果绘制在图 12 中的相平面。在这个平面中可视化，准平衡轨迹在相空间中缓缓弯曲。测得的状态在所有点上都保持接近参考轨迹，保持在与图 4 所示大小相似的区域内。这让我们有很好的信心，对于沿该轨迹的每个工作点，线性化很好地代表了动态行为。此外，这些结果验证了从图 5 中得出的关于平滑变化动力学的结论。即使使用的所需平衡和线性化发生变化，车辆也会保持路径。
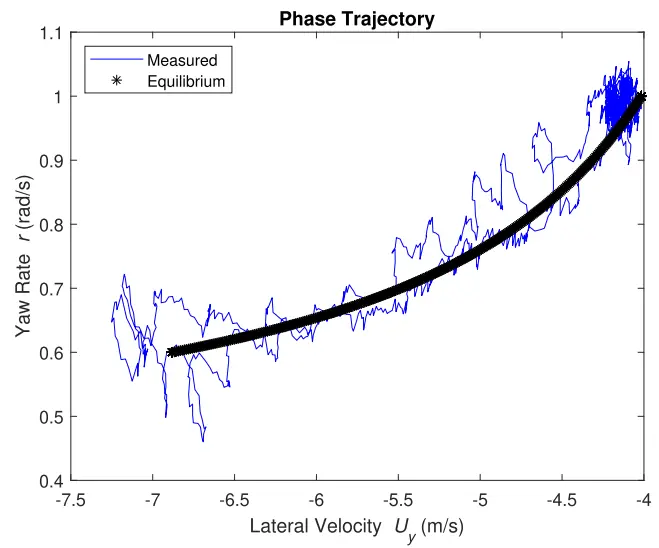
图 12.来自图 13 所示的同一准平衡实验的数据在相位平面。黑色星号表示准平衡路径上的平衡，而蓝线表示测得的状态数据。即使参考平衡在整个相位平面上移动，状态仍然接近平衡。
图 13 显示了准均衡实验的状态跟踪数据。尽管漂移平衡发生变化，这会导致平衡横向速度和偏航率发生巨大变化，但无人机以最小的误差跟踪状态。对于此数据集，RMS 横向路径跟踪误差为 3.7 cm。状态中最大的误差发生在 52-55 秒左右，就在车辆达到 12 m 半径漂移并且平衡横向速度和偏航率达到拐点之后。对 52-55 秒左右的误差的可能解释来自图 14 所示的纵向速度控制器结果。
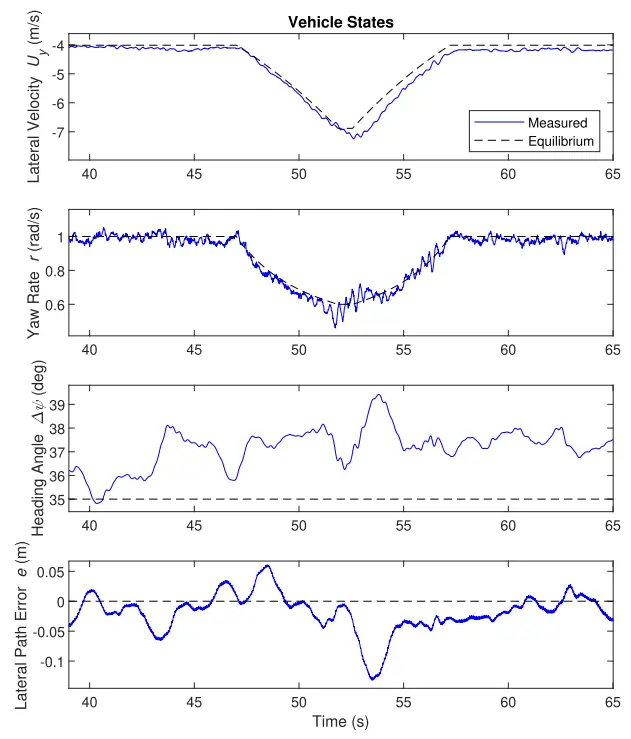
图 13.遵循准平衡轨迹时收集的数据。蓝色线条表示测量值，而黑色虚线表示平衡值。控制器保持近距离路径跟踪 - 表现在两个航向中与平衡的低偏差，和横向路径跟踪误差同时紧紧跟随漂移平衡逐渐变化的轨迹。
图 14. 纵向速度控制器状态和准平衡实验的输入。测量值以蓝色显示，命令输入以红色显示，平衡值由黑色虚线显示。
如图 14 所示，前制动器在纵向速度增加和减少时调节纵向速度。此图揭示了此控制器的局限性。前制动器控制纵向速度，而不是油门，因此控制器提高纵向速度的唯一方法是松开制动器。虽然这种控制策略总体上有效（该数据集的 RMS 速度误差仅为 0.34 m/s），但当参考速度增加时，纵向速度中最大的一致误差会出现，大约在 47 到 53 秒之间。纵向速度误差的这种积累可能导致图 13 中其他状态的误差。
图 15 显示了稳定的 LQR 输入。平衡值和命令输入值之间的偏差是由于控制器稳定漂移，即使测量状态与所需状态不匹配也是如此。
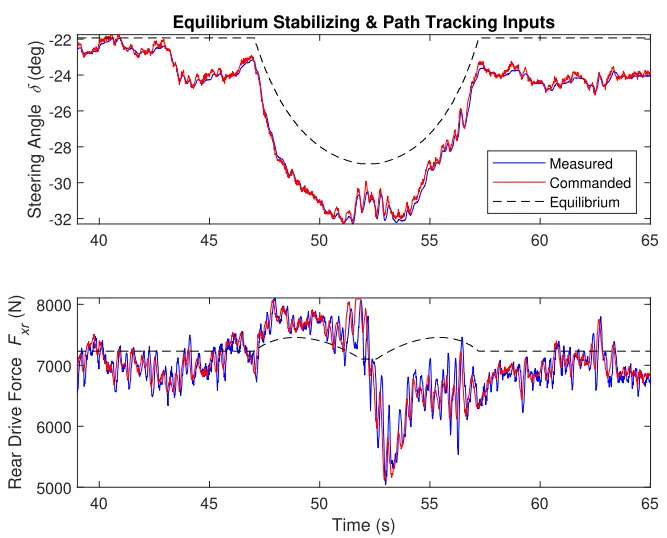
图 15.实验的转向角和后驱动力输入如图 13 所示。输入的测量值以蓝色显示，命令值以红色显示，平衡值用黑色虚线显示。
尽管依靠制动器来控制纵向速度和足够精确的参数以避免重大的稳态误差存在局限性，但该控制器的整体性能非常出色。这种方法在具有大量工作点的轨迹上的成功证明了状态空间漂移区域中动力学的线性性和平滑性。
广告
广告
编辑推荐
最新资讯
-
纽北（Nürburgring Nordschleife）赛道介
2024-11-22 09:17
-
虚拟验证先行丨集成多学科方法，让电池生产
2024-11-22 09:10
-
新品上市 | Fusion-LN 数据采集的下一个飞
2024-11-22 09:08
-
车规级V2X芯片- 汽车移动通信功能核心
2024-11-22 09:03
-
BEV端到端视觉论文合集|从不同的视角解析BE
2024-11-22 09:00
广告
广告
