利用线性结构对高度非线性的车辆动力学进行精确控制

线性化适当性的最后一个测试是查看线性化系统是否以直观的方式响应增益变化。微调 LQR 控制器的一种方法是选择与平衡值的最大可接受偏差相对应的协方差，如 （14） 和 15 所示。对于输入，与平衡值的最大可接受偏差本质上是最大可接受反馈。

由于更改了Q矩阵或R矩阵调整所有增益，一个简单的测试是改变一个输入的最大可接受反馈，看看闭环系统是否用另一个输入进行补偿。图 16 和图 17 显示了在 的最大可接受反馈沿轨迹变化时稳定平衡的实验结果。代表最大可接受反馈值的每个协方差对应的增益在大约一圈内保持不变。每幅图中的垂直线表示增益发生变化的时间。实验显示，所有其他和项保持不变，包括最大可接受反馈.

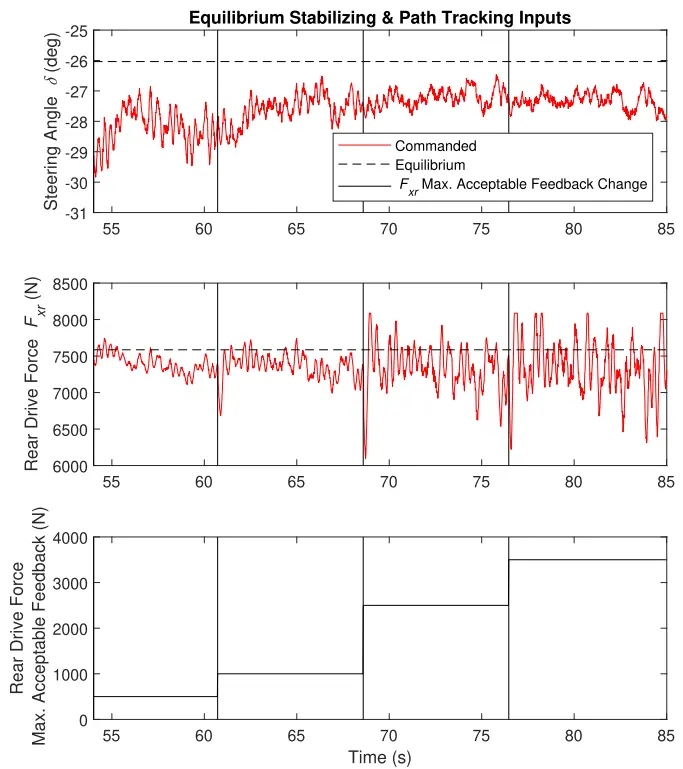
图 16.当跟踪各种最大可接受反馈值的单个平衡时，转向和油门输入.顶部两个图以红色显示输入命令，平衡值为黑色虚线。每个图中的垂直线表示何时改变。底部图显示了。请注意，作为增加，则命令增加和命令减少。

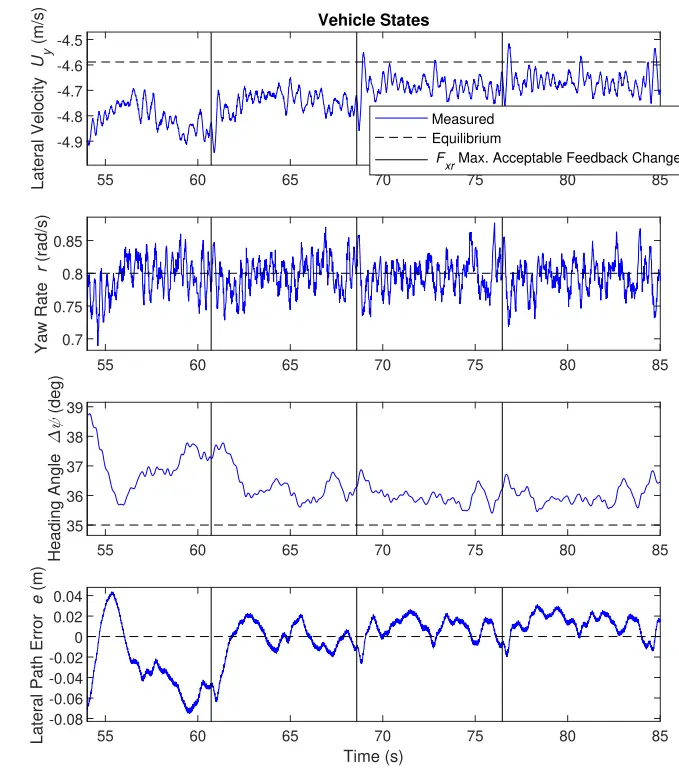
图 17.状态跟踪性能，用于跟踪各种最大可接受反馈值的单个平衡.通过 LQR 控制的四种状态以蓝色表示测量值，以黑色虚线表示平衡值。每条垂直线表示.的四个不同的最大可接受反馈值分别为 500 N、1000 N、2500 N 和 3500 N，如图 16 的最底部图所示。

由于 LQR 设计中的所有权重都是相对的，减少一个输入的最大可接受反馈量将要求控制器更加依赖另一个输入。实验结果恰恰证明了使用和以稳定车辆。如图 16 所示，随着最大可接受反馈值的增加，指令的可变性增大，而  指令的可变性减小。只需调整矩阵的一个元素，控制器就能做出直观的响应。

图 17 显示了 R 矩阵调整实验中的四种 LQR 状态。在的四个不同的最大可接受反馈值中，则第一个最大可接受反馈值似乎过低。由于控制器需要更多的来减小状态误差，因此该部分的四个状态误差都较大。随后的三个最大可接受反馈值产生了令人满意的状态跟踪结果。因此，决定的最大可接受反馈值仅仅是两个输入指令所需的可变性问题，可以在此范围内任意选择一个值。

   Ⅵ 讨论    

与其他跟踪所需准平衡路径 [6]、[5] 的漂移控制器相比，该控制器可实现更准确的路径跟踪结果，特别是要低得多的 RMS 横向路径跟踪误差。Goh 等人实现了 18 cm 的 RMS 跟踪误差 [5]，Goel 等人实现了 42 cm 的 RMS 跟踪误差 [6]，而该控制器的 RMS 跟踪误差仅为 3.7 cm。我们介绍的方法的优势在于线性模型控制技术的广泛应用。虽然 Goh 和 Goel 依赖于非线性模型和特别选择的误差动态，而这里开发的控制器是一个基于线性模型的 LQR 控制器，外加一个比例反馈加前馈回路。LQR 技术无需严格遵守任意误差动态，因此会产生更好的跟踪结果。此外，这种简单明了的控制器还便于直观地选择和调整输入权重。

图 18 显示了 [5] 中描述的非线性控制器与此处开发的线性控制器之间的更直接比较。实验从非线性控制器开始，然后在大约 23.4 秒时切换到线性控制器。虽然此数据集开始时使用的非线性控制器成功地实现并保持了所需的状态，但当线性控制器接手时，路径跟踪会得到显著提高。采用线性设计后，路径跟踪性能得到了明显改善。相比之下，在非线性控制器中，增益选择与路径跟踪之间的联系就不那么清晰了。正是由于这种清晰性，我们才能为简单的 LQR 控制器找到一组线性增益，从而使其性能优于基准非线性控制器。

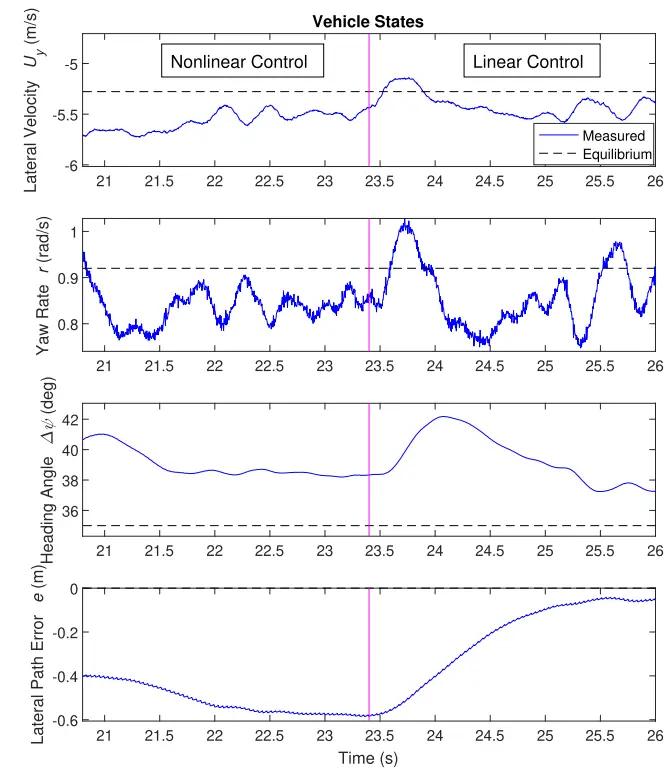
图 18. 用于跟踪平衡轨迹的不同控制器的比较。蓝色线表示测量值，黑色虚线表示平衡值。实验开始使用 [5] 中描述的非线性控制器，然后在洋红色垂直线指示的时间切换到本文中描述的线性控制器。

 Ⅶ 结论和未来工作    

漂移平衡点附近相当大的区域内的动力学可以用线性化动力学进行合理的近似。这就允许使用经典的线性控制技术（如 LQR）来精确控制漂移车辆的状态和轨迹。

未来工作的一个方向是将执行器动力学纳入车辆模型。并非车辆上的所有系统--发动机、制动器和转向系统--都以相同的速率响应。将执行器动态纳入模型可避免执行器之间的相互影响，并有可能带来更好的结果。用于演示该控制器的车辆是电动的，可以提供近乎瞬时的扭矩；但内燃车辆在提供必要扭矩时会有不可忽略的延迟。这可能需要额外的建模，特别是完成更多的瞬态机动。为了捕捉内燃机的动态，我们可能需要增加状态矢量，将轮速或发动机速度包括在内，然后在内燃机车辆上测试这种新控制器。

这里介绍的线性化模型也可以在模型预测控制 (MPC) 框架中实施。由于我们已经证明，在对非线性系统进行线性化后，我们可以对其进行控制，因此我们现在可以使用许多与非线性系统不兼容的分析工具。在这里，线性化模型将使我们能够研究不确定性；管控 MPC 是量化不确定性并提出相关主张的一个可能途径。此外，如果我们将纵向速度作为一个状态，并将制动力作为一个输入，则可以使用 MPC 框架来获得对纵向速度的更多控制。

该控制器实现的状态和路径跟踪精度表明，漂移并不是需要避免的状态空间区域。通过实施基于线性化模型的控制器，我们取得了比使用更复杂的非线性模型开发的控制器更好的路径跟踪结果。对于漂移车辆的控制，我们还有很多需要了解的地方，这里介绍的线性化模型是我们在了解并最终利用状态空间的这一不稳定区域方面迈出的重要一步。

 附录   

力计算

由于无法直接测量轮胎受力，我们对轮胎受力进行了如下估算。

我们使用轮胎纵轴与 Goh 等人在 [5] 中定义的总力矢量之间的夹角作为推力角，将后轴上的总力分解为纵向力和横向力。推力角是当前状态的函数，包括后轮速度和包括后轮半径在内的车辆参数。

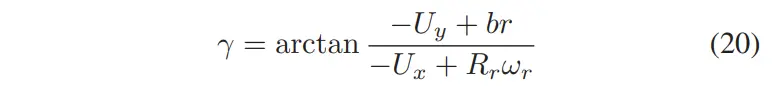
为了通过推力角将轮胎力联系起来，我们假设后轮胎在滑动时。然后我们计算后轮的横向和纵向力

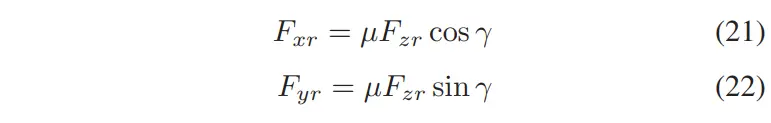
重新排列运动方程 (1)-(3)，我们就得到了一个由三个方程和两个未知数组成的线性方程组。

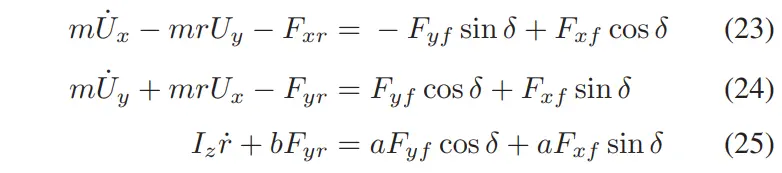
使用 MATLAB 中的 Savitzky-Golay 滤波器计算、和 的导数。

参考文献

责编丨高炳钊