广告
基本载荷分析方法
穿级计数的法则非常简单：如果一个载荷在变化的过程中（载荷上升或下降），“穿过”了（跨越了）某一载荷水平线，就在相应的载荷水平线上计数一次。这种穿级计数，用symmetric加以标识。如果在穿级计数过程中，只考虑到载荷在上升的过程中对于某一条载荷水平线的跨越，那么这种计数常称为“上升沿”穿级计数，在TecWare软件中用DIN加以标识（代表DIN 45667标准）。
图3-6 穿级计数法则示意图2
穿级计数的局限性由图3-7可以显现出来。两个完全不一样的载荷，通过穿级计数结果将是一样的。
这样一种逻辑简单的计数方式有什么作用呢？实际上，穿级计数与频域疲劳寿命评估有着密切的联系。为了讲单轴电磁振动台加速试验方法，在后面会谈到对于稳态高斯随机过程的窄带频域疲劳寿命评估模型，当理解了这个模型之后，就会明白穿级计数存在的意义。两个相似的高斯随机振动过程，其时域信号的穿级计数结果的形态应该是相似的。
图3-7 穿级计数结果的局限性2
3.1.1.4 峰谷值计数
峰值计数也非常简单，一句话就可以说明白：峰值计数是对一段随机时域信号“极大值”点和“极小值”点的计数结果，如图3-8所示。峰值计数的局限性如图3-9所示。两个完全不一样的载荷，峰值计数的结果会一样。
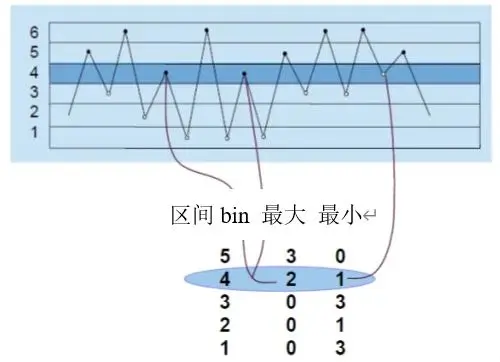
图3-8 峰值计数法则示意图2
图3-9 峰值计数结果的局限性2
峰值计数结果主要用来反应载荷对于结构可能造成的响应边界和极限。由于“极值”与“最值”之间的天然联系，峰值计数结果的一个重要应用是借助于“极值点”的统计分布信息，构建和获取“最值”的统计分布信息。
这里不加证明的给出一个与之相关的重要统计学结论（有兴趣的读者可以自行证明一下1）：
设X1,…,Xn独立同分布，X1有分布函数F(x)和密度函数f(x)。记
Y = max (X1,…,Xn)，Z = min (X1,…,Xn)
则Y和Z分别有概率密度函数nFn-1(x)f(x)和n[1-F(x)]n-1f(x)。
3.1.1.5 旋转扭矩直方图计数
3.1.1.5.1 区分“花键”和“齿轮”
在道路载荷数据采集活动中，容易通过传感器或CAN总线获取传动系统上某一部位的转速和扭矩时域数据，这个是对于（比如说）变速箱齿轮的弯曲疲劳问题进行分析的载荷输入。
尽管花键和齿轮都是旋转部件，但是需要从载荷波动与其旋转行为是否相关这一角度，来区分这两类旋转部件。对于“花键”和传动轴承受的扭矩是与其旋转行为无关的，因此，对于“花键”和传动轴进行扭矩载荷计数，使用传统的雨流计数就可以，没有任何新的技术。齿轮则不一样，由于齿轮上的每一个齿，每旋转一周要啮合一次，因此，齿轮上每一个齿所承受的载荷波动与其旋转行为有密切的关系。相对于传动轴和“花键”来说，齿轮的旋转使其所承受的载荷呈现高频波动的特征，波动的频率与齿轮的转速直接相关。
想象一下：如果一辆车以匀速在平直的公路上行驶，这时候，车辆的传动系统所承受的扭矩是稳定的。最理想的状况下，传动轴所承受的扭矩时域曲线会“拉平”成一条水平线。也就是说，在这种理想的状态瞬间，传动轴不存在疲劳问题，只存在强度问题。但是，即使在这种理想的瞬间，由于齿轮的旋转，仍然会使得齿轮上的每一个齿承受一个高频波动的周期性载荷，从而对于齿产生弯曲疲劳的问题。这个是“花键”和“齿轮”非常不一样的地方，导致相应的载荷谱处理完全不一样，也导致了针对于齿轮载荷谱分析时需要用到的旋转扭矩直方图计数的产生。
3.1.1.5.2 旋转扭矩直方图计数原理
旋转扭矩直方图计数的原理并不复杂。如图3-10所示，把扭矩时域数据按照扭矩（纵轴）切分成很多的bin（小的区间）。如果bin切分的数目足够多，则每个bin都会足够小，或者说在每个bin内扭矩基本处于一个恒定水平。紧接着，如图3-10所示，需要找出与扭矩处于某一恒定状态所对应的时间区间。在这些时间区间内，转速随时间的变化关系也是有的。因此，如图3-10所示，对于相应时间区间内的转速进行积分和累加，得到转角，最终除以2π，则如图3-11所示，获得在某一恒定扭矩状态Ti下，齿轮转过的圈数ni。
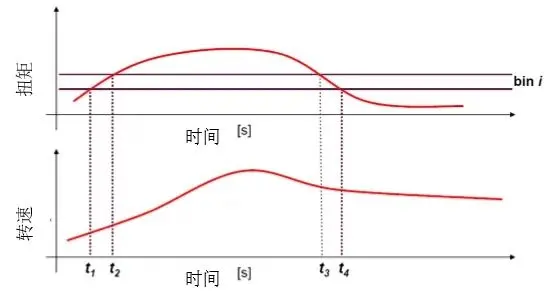
图3-10 旋转扭矩直方图计数原理2
广告
广告
最新资讯
-
厂商要多努力，才能让用户听起来毫不费力？
2024-11-22 17:10
-
TOP30！海克斯康入选2024福布斯中国数字科
2024-11-22 15:25
-
揭秘国产装备制造厂商的成功秘籍：好耐电子
2024-11-22 15:24
-
一文详解安全分析方法STPA：以自动紧急制动
2024-11-22 15:20
-
选对涉氢压力表：守护涉氢场所安全的关键一
2024-11-22 15:19
广告
广告
