新能源汽车车载系统中的滑膜控制简述

一、概述

滑模控制（Sliding Mode Control, SMC）是一种非线性控制方法，能够处理具有复杂动态特性的系统，因其鲁棒性强、抗干扰能力强、快速收敛等特点，在新能源汽车的如电机控制、车辆动态控制、电池管理系统SOC估计、电池温度控制以及能量回收等车载系统中被广泛应用。

二、滑膜控制设计步骤

2.1.定义滑模面

滑模面函数s(x)是一个关于系统状态变量x的函数，它描述了系统沿着滑模面运行的特性。在滑膜控制中，s(x)函数的选择直接决定了系统能否快速进入滑模面并在滑模面上稳定运行。该函数在选择上通常需结合系统的动态特性、控制目标以及系统的稳定性要求。在车载系统中，根据系统应用特性，常见的滑模面函数定义方法有：

1）基于误差的滑模面

该滑模面函数可基于系统状态误差来定义，如s(x)=e(t)或

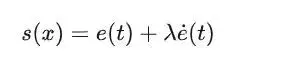
其中，e(t)=r(t)-y(t)表示误差信号，r(t)是系统期望的输出，y(t)是系统实际的输出，λ是系统设计参数，用于调整系统的收敛速度和稳定性。该滑膜面函数适合于需要跟踪误差快速收敛到零的系统，如电机转速控制等。

2）基于系统状态的滑模面

该滑模面函数可直接基于系统状态变量来定义，如s(x)=x1+x2。

其中x1和x2分别是系统的两个状态变量。该函数适用于需要控制多个状态变量的系统，如悬架系统、制动系统、车辆动态系统等。

3）基于高阶导数的滑模面

顾名思义该滑模面函数包含系统状态的高阶导数，如：

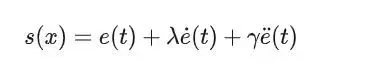
其中，γ是系统的另一个设计参数。该类型函数适用于需要控制状态变量的高阶导数，以提高系统的动态性能和响应速度的场景，如飞行器姿态控制、发动机控制系统和传动系统控制等。

在定义滑模面函数时，首先需要明确系统想要达到的控制目标，如误差趋近于零、系统状态稳定等。接着通过分析系统的动态特性，以了解系统的状态变量、输入/输出关系等，并考虑系统中存在的不确定性和干扰因素。基于控制目标和系统特性，再选择合适的滑模面函数形式。

2.2.设计控制律

根据选定的滑模面函数s(x)去设计滑模面函数的具体表达式，以确保系统能够在有限时间内达到滑模面，并在滑模面上稳定运行。该步骤主要包括两部分：等效控制律ueq和切换控制律usw。

2.2.1.等效控制律设计步骤

1）计算滑模面函数的导数

以单输入单输出的驱动电机控制中基于误差的滑膜面函数为例，计算其导数，并代入其动态方程①

其中：ω是电机实际转速；ω导数（）是转速的变化率；u是电机的输入电压，由电机控制器控制输入；a和b是系统参数；d是外部干扰或不确定因素。

和转速误差e(t)=r(t)-ω(t)，

其中，r(t)是整车期望转速，该值来源于对加速踏板信号的解析。

可得到s(x)的导数表达形式：

2）设计等效控制律

为了消除系统中的确定性因素（如系统参数和已知的外部扰动等，使系统在滑模面上的行为仅由不确定性和外部干扰决定），确保系统能够在滑模面上稳定运行，此时等效控制律ueq应满足s(x)的导数等于0，即

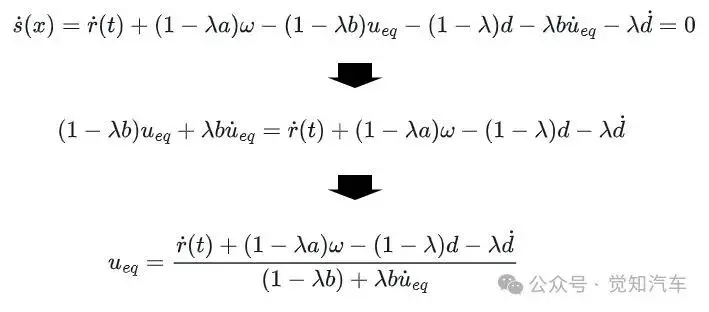
通常情况下，会设定ueq的导数近似于零，因此等效控制律可简化为：

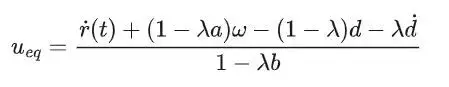
注：等效控制律ueq代表在期望转速下电机所需要的输入电压，即一个期望的输入电压值，其目的是消除系统中的确定性因素，以确保系统能够在滑模面上稳定运行。

2.2.2.切换控制律设计步骤

切换控制律usw是一个附加的控制信号，其目的是克服系统中的不确定性和外部干扰，确保系统能够在有限时间内快速达到滑模面。其通常包含一个切换项-k*sgn(s(x))。

1）选择切换增益k

切换增益K值影响系统的收敛速度和稳定性，通常，K值需要足够大，以克服系统中的不确定性和干扰，但又不能因值过大而引入不必要的高频振荡，因此该值的选择需要通过反复试验、仿真以确保其准确性。

2）切换控制律

在驱动电机转速控制中，切换控制律通常可以表示为：

usw=-k*sgn(s(x))

其中sgn (s(x))可定义为：

2.3.总控制律

总控制律u(t)是等效控制律ueq和切换控制律usw的组合，代表电机的实际输入电压（电机控制器通过调节后输出的电压）。其作用便是结合了等效控制律ueq和切换控制律usw的两者功能，即确保系统能够在有限时间内到达滑模面，并稳定运行。

在表现形式上，总体控制律u(t)= ueq+usw，即：

在设计好控制律后，通过数学函数分析等方法证明该控制律确实能够保证系统的有效性，并通过实验或仿真进行调试，以验证实际控制效果。

三、电机控制实现过程

在控制电机运行的初始阶段，此时系统远离滑模面（即实际转速与目标转速存在差距），电机转速误差e(t)和其变化率‘e(t)的导数’都还较大，此阶段下通过切换控制律usw的作用，以克服系统中的不确定性和外部干扰，让系统能够快速收敛到滑模面，即快速到达期望转速。

当系统逐渐接近滑模面时，转速误差e(t)和其变化率开始逐渐减小，此过渡阶段下等效控制律ueq和切换控制律usw共同作用，确保系统稳定地达到滑模面。

当系统已经位于滑模面上后，转速误差e(t)和其变化率都接近于0，此时电机的实际转速与期望转速基本一致，在此稳态下，usw继续发挥作用，克服系统干扰，此时总控制律u(t)将极限接近等效控制律ueq的值。

图1 滑膜控制在电机转速上的应用示例

注：在车载系统中，基于转速差实现对驱动电机的控制，根据应用及策略的不同，还需要考虑如实时性要求、故障保护机制以及与其他系统的集成等。

四、与双环控制的差别

在传统的电机控制策略中，多采用转速环套电流环的双闭环控制策略。首先，在双环系统中，外环为转速环，主要任务是控制电机的转速，内环是电流环，通过接收外环的期望电流，从而控制电机绕组中的电流。对于该电流的控制，常又会嵌套一个电压环，以控制逆变器的输出电压，从而到达控制电流的目的。基于此控制方式下的内外环配合，能够实现更高的控制精度。

而滑模控制通常不采用这种双闭环结构，其通过对逆变器输出电压的直接控制，来直接改变电机的输入电压，此单环控制方式让其不需要额外的电流环，使得控制结构更加简单，同时具有更强的鲁棒性和更快的动态响应能力，更适合那些需要快速响应、系统存在较大不确定性或外部干扰的应用场景

五、总结

在实际车载系统的应用中，滑模控制因其简单高效的特性，在电机控制领域得到了广泛的应用，特别是在需要快速响应和鲁棒性的场合。但在应对不同需求和应用场景时，还需根据实际情况去选择控制策略。如对控制精度和稳态性能有严格要求的场景，常以双环控制为主要应用，而在需要快速响应和较强鲁棒性的需求下，滑模控制则是更好的选择。或根据实际需求，通过多控制策略结合应用，以获得更好的整体性能。

①对于驱动电机的转速控制而言，动态方程可从电机的物理原理出发，通过电磁转矩、电机机械转矩平衡以及电机绕组中的电压、电流及反电动势之间的关系推倒出。在常规应用中，通常可简化为：