鱼眼相机在自动驾驶环境感知的应用和挑战
3)正投影:与之前的投影模型相似,正投影以对球体的投影开始(图5c)。接下来是对该平面的正交投影。因此,正字法投影是由
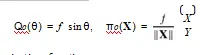
未投影函数为
这里是I 2 = R2、C3 = {X∈R3 | Z > 0}和θmax = π/2。这些非投影函数被定义得很好,如f≥Ⅱu Ⅱ,它是由原始投影(10)强制执行的。
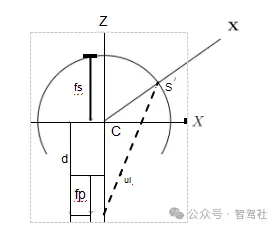
4)扩展正交模型:扩展正交模型[33],如图5d所示,通过释放投影平面与投影球的正切关系来扩展经典正交模型,允许偏移λ。扭曲投影与方程(10)相同。而失真的和未失真的径向距离与其逆距离之间的关系则由
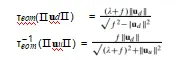
这是在[33]中稍微简化的表示,并假设f和(λ + f)是正的,这完全是实际的约束。扩展的正交法模型与标准正交法模型具有相同的域和共域。

图5。经典的几何模型。
5)扩展等距模型:实际上,扩展的正交图模型只是一个从投影到图像上映射的转换。许多模型可以以与扩展的正交法模型相同的方式转换为图像上的映射。我们只给出了等距模型的一个例子。
重新排列(4),使θ = ⅡusⅡ/f替换为(2),使(2)的焦距为f +λ,得到等距模型的图像上映射。按照类似的步骤,我们也可以得到逆的结果。
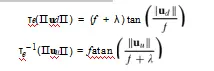
这在[34]中描述了,尽管没有额外的缩放参数λ。我们也可以遵循上面相同的步骤来获得一个扩展的立体模型。这些扩展模型的C3、I2和θmax与正交法模型相同。
D. 代数模型
我们提供了一个简短的讨论鱼眼相机的代数模型,特别是多项式模型,和二模型。多项式模型的讨论,我们提供的完整性,虽然我们集中在几何模型的其余部分。
1)多项式模型:非鱼眼相机的经典布朗-康拉迪畸变模型[35],[36]使用一个奇称为多项式,ⅡudⅡ = Pn(ⅡuuⅡ),来描述图像上的径向畸变(即映射ⅡuuⅡ到ⅡudⅡ),其中Pn表示一些任意的n阶多项式。尽管年代久远,但布朗-康雷迪模型是非鱼眼相机[37],[38]的软件实现中的标准失真模型。为了解释鱼眼失真,在[18]中提出了一种图像上的多项式模型,称为多项式鱼眼变换(PFET)。PFET和布朗-康雷迪模型之间的区别在于,PFET允许奇数指数和偶数指数来解释在鱼眼相机中遇到的额外失真。
存在一类多项式鱼眼模型,其中场角到像平面的映射是通过a
多项式,即QP (θ) = Pn(θ),使用入射角而不是未失真的半径。例如,坎那拉-勃兰特[20](以及在流行的OpenCV软件[37]中实现的那样)提出了一个n = 5或更多阶的多项式模型,只有奇指数。在[2]中,提出了一个同时包含偶指数和奇指数的n个=4多项式。这两种模型都没有在多项式中使用常数系数项,因为这样做会导致在图像的中心有一个未定义的区域。在[39]中提出了一个五阶多项式,但如果鱼眼半径和视场已知,则将其简化为四个独立参数。以上这些都可以解释为等距模型的推广,这是一个一阶多项式。在这种情况下,投影球被给定多项式定义的曲面所取代。然而,这是迫使一个几乎没有效用的几何解释。
MATLAB计算机视觉工具箱[40]和NVidias驱动系统的SDK [41]包括了在[42]中提供的基于多项式的鱼眼模型的实现。在这种情况下,多项式被用来建模投影和非投影,否定了需要一个数值方法来反转投影(这是基于多项式的模型的一个主要计算问题)。注意,这两个多项式并不是相反的,而是两个不同的函数。这些多项式是独立校准的,这可能使它无法使用的迭代方法,如果多次项目和取消项目点。
2)分割模型:径向分解的分割模型[17]获得了一些良好的特性,至少对于单参数变体,直线投影到图像[43],[44],[45],对于许多镜头,单参数变体的[46]表现很好。该模型及其逆模型由
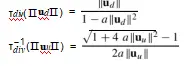
这在[34]中通过添加了一个额外的扫描参数进行了扩展,从而提高了某些类型的鱼眼透镜的建模性能。而划分模型
最初以图像上映射表示,它可以表示为投影函数
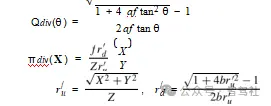
将针孔模型(2)代入(16),得到径向投影函数Q div(θ)。f,在这种情况下,一旦被分割模型解决了失真,就可以被认为是针孔模型的参数。分割模型的非投影为

投影函数和图像上映射具有相同的域,C3 = {X∈R3 | Z > 0}、I 2 = R2和θmax = π/2。
E. 球形模型
基于对一个单位球的点(或其仿射基因化)的投影,我们也考虑了一组最近的(至少是过去几十年的)鱼眼模型。
1)视场模型:视场模型[19]及其逆模型的定义为
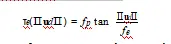
参数ω近似于相机的视场,虽然不是完全的[19]。这是一个图像上的模型,就像分割模型一样,其中ⅡuuⅡ和ⅡudⅡ定义了图像平面上的未扭曲和扭曲的半径。或者,它也可以被表示为一个投影函数[23]。
非投影是由
将视场模型表示为投影函数的一个很好的结果是投影πfov (X)的域
覆盖所有C3 = R3 \(0、0、0)T。相比之下,视场模型的图像上映射形式仅限于映射C3 = {X∈R3 | Z > 0}中的图像点,这对任何图像上映射都是如此。成像点的集合是I 2 = {u∈R2|ⅡⅡ≤θmax = π。我们将很快证明视场模型是等距模型的等价物,因此是一个球形投影。
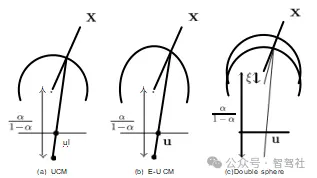
2)统一相机模型:UCM最初用于建模散照相机[21],后来被证明在建模鱼眼相机[47],[48]。它已被证明在一系列的镜头[46]上表现良好。首先,点X被投影到一个单位球体,然后投影到一个建模的针孔相机(图6a)。我们提出了具有更好的数值性质的版本。

图6。球形模型。UCM (a)首先是对单位球体的投影,然后是透视投影。E-UCM用一个椭球体代替了球面,其系数为β。DS模型在UCM上增加了第二个单位的球体投影,球体之间的距离为ξ。
UCM的非投影由
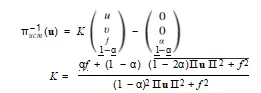
编辑推荐
最新资讯
-
大卓智能端到端直播实测,16公里复杂路段挑
2025-04-25 17:16
-
《汽车轮胎耐撞击性能试验方法-车辆法》等
2025-04-25 11:45
-
“真实”而精确的能量流测试:电动汽车能效
2025-04-25 11:44
-
GRAS助力中国高校科研升级
2025-04-25 10:25
-
梅赛德斯-AMG使用VI-CarRealTime开发其控制
2025-04-25 10:21





 广告
广告





























































