鱼眼相机在自动驾驶环境感知的应用和挑战

因此，这里并没有显示出来。投影的结构域和径向函数为

当α<为0.5时，针孔投影点在单位球体内，当α>为0.5时在外部，当α=为0.5时在球体上。

3)增强统一相机模型：UCM由增强UCM[22]（图6b）扩展，它将球形投影推广到一个椭球体（或者，实际上，是一个一般的二次曲面），并能够证明一些精度增益。E-UCM是由

其中，d=√β（X2+Y2）+Z2，β为椭圆系数-

cient.非投影函数对于EUCM来说并不漂亮，读者可以参考的是[22]。有效的点和角度的集合为

4)双球体模型：后来，UCM再次被双球体（DS）模型[23]扩展，它增加了第二个单位球体投影，以实现更复杂的建模（图6c）。

在[23]中给出了令人信服的结果，以证明了双球模型的有效性。该模型的非投影函数为

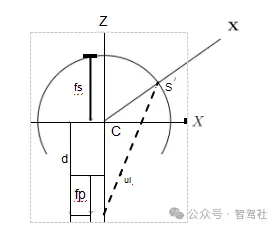
图7。一般透视映射的定义是由一个点到半径为fs的球体的投影，然后是到焦距为fp的针孔模型的透视投影。这两个投影中心被d偏移。与经典模型一样，它在制图学中被知道了几十年的[53]。

投影和非投影的有效范围为

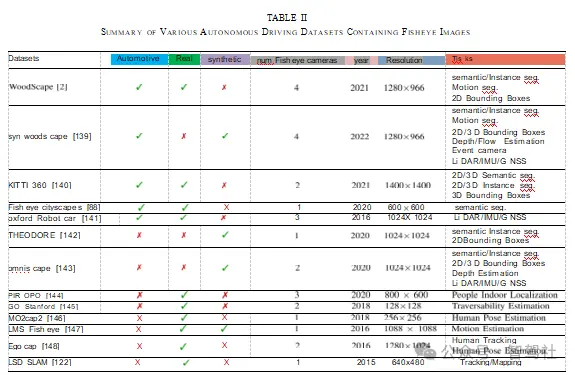
F. 其他型号

虽然我们已经讨论了许多更流行的鱼眼投影模型，但这并不是详尽的。无论出于什么原因，我们省略了一些似乎不太受欢迎的模型的细节。例如，巴克斯坦和Pajdla [49]提出了对经典模型的两个扩展。在[18]中也提出了一种基于对数的鱼叶眼变换（FET），尽管与其他模型相比，其精度较低。[50]中提出的基于双曲罪恶的广角摄像机[51]模型，后来用于它，这里没有讨论，也没有级联单参数分割模型[52]。

G. 照相机型号的统一使用

随着鱼眼模型的普及，人们很自然地会怀疑一些模型之间是否存在共性，甚至在模型的开发过程中是否存在重复。

1)一般透视投影和鱼眼模型：

统一相机模型属于一类球体的一般垂直透视投影，在测测量学和制图领域中有[53]，[54]，其中在球面上添加了中心投影的平凡步骤。立体投影和正交投影也属于这一类。立体投影的针孔投影中心是在球体的表面上，而正字法投影具有无限的焦距（因此称为术语正字法）。立体投影和UCM之间的联系实际上在[21]中描述。

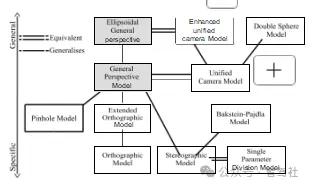
图8。各种鱼眼模型与一般透视投影之间的关系。双线表示两个模型是等价的，单行表示泛化/专业化。

让我们首先检查图7所示的一般垂直透视投影，。针孔相机沿z轴偏移一个距离d。到球面上的投影是由

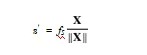
这里我们使用s =（x，y，z）T表示半径为fs的球上的点，以便将其与之前用来表示单位球上的点区分开来。点u是s的针孔投影

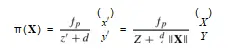
+d将这些点从球体转换为针孔坐标系。因此，通过这两个参数γ = fp和ξ = d/fs，我们有（24），UCM。另外，如果我们将针孔相机平面限制在球面表面（即d = fs），并制作fp = 2fs，我们得到立体方程(7)。

E-UCM [22]通过投影到一个椭球体而不是一个球体来扩展UCM。这种类型的投影在测地学和制图学中被称为[53]，[54]椭球一般透视投影。我们不会在这里重新推导方程，而是让读者参考原始材料。如前所述，DS模型[23]通过添加第二个投影球来扩展对更复杂的光学进行建模的UCM。

因此，鱼眼镜头的UCM、E-UCM和DS模型可以作为立体图像相机模型的推广。更正确的是，它们所有模型（UCM、E-UCM、DS、分割模型和立体模型）都是一类一般透视模型的一部分。如果我们允许fs接近于无穷大，那么（40）就成为了针孔投影模型。如果我们允许fp（因此也允许d）趋于无穷，那么我们得到正投影。

2)立体图和除法模型：正如在[55]中所讨论的，我们可以将针孔投影(2)与逆立体模型(8)给出

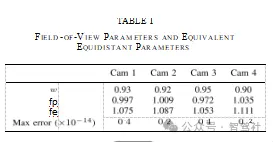
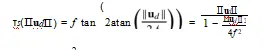
允许一个= 1/4f 2，这与分割模型相同，（16）。因此，我们可以说，分割模型是立体投影的图像上版本。

3)等距和视场模型：考虑(2)给出的径向针孔投影，以及等距鱼眼投影模型(4)。将这两者结合成与视场模型相似的形式（19）

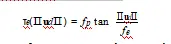
由于fp和fe是自由参数，通过计算法确定，我们可以将其设置为

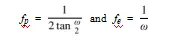
因此我们可以看出，（19）式和（42）式是等效的映射函数。视场角模型是等距投影的基于图像的版本。

结果：为了具体证明球极平面投影 / 除法模型对以及等距投影 / 视场角模型对的等效性，我们给出了一组小规模的结果。值得一提的是，[23] 中提供了五台相机的一组参数，其中包括视场角模型的参数。根据 [23] 中视场角模型的参数集 ω，我们通过应用（43）式来获取等距参数。见表一。两者之间的差异处于机器精度级别，这证明了这两个模型是等效的。[46] 中呈现的结果（特别是参考表四）支持了球极平面投影模型和除法模型的等效性。我们可以从中看到，当将球极平面投影模型与除法模型进行对比时，残差为零。我们还可以看到，当将统一相机模型（在 [46] 中称为通用传感器模型），或者等效地说将通用透视映射与球极平面投影模型和正射投影模型进行对比时，残差也为零。

讨论：鱼眼相机应用存在大量潜在的模型。在本文中，我们提及了二十种模型，不过可以肯定的是这并不详尽。然而，我们已经表明许多几何模型之间存在很强的关联性。至少有七种模型与通用透视投影相关或直接等效。此外，我们还表明一些近期开发的鱼眼模型在数学上与经典鱼眼投影是等效的。

图 9. 环视相机可视化效果

几十年前提出的球极平面投影和等距模型等功能。在图 8 中，我们给出了与通用透视投影相关的几何鱼眼模型示意图。

三、环视相机系统

在本节中，我们将讨论环视相机（SVC）的设置及其感知所需的基本要素。我们先从环视相机用于可视化的历史应用情况入手，这有助于理解汽车配置情况。然后我们再讨论诸如校准、校正以及几何基元等支撑模块。

A. 可视化

从历史上看，环视相机一直用于在驾驶员仪表盘上显示，以实现泊车可视化。首个可视化应用展示的是一个用于倒车辅助的后视鱼眼相机 [12]。之后通过对行人、行车道等物体检测的可视化，该应用得到了进一步改进 [56]，随后利用四个鱼眼相机将其增强为环视可视化 [57]。最初的系统基于二维俯视图，如图 9（a）所示。这主要用于泊车应用，但也可用于其他如交通拥堵辅助等低速操控应用场景。二维俯视图假定地面是平坦的，所以当地面有起伏时就会出现伪影。其他附近物体（如车辆）在这种视图下会严重失真。通过采用一种类似碗状的曲面（其中心附近是平坦的，朝周边呈向上弯曲状）构建的三维环视视图解决了这些问题，如图 9（b）所示。此外，利用车辆周边的深度估计可以调整碗状曲面，以实现最佳视角，减少附近物体的伪影。例如，如果车辆一侧有其他车辆靠近，该区域的碗状曲面就会移到本车前方以避免产生伪影。通常，应用程序会提供一个用户界面，供驾驶员动态选择所需的视角。环视可视化应用通常是作为一个利用图形处理单元（GPU）的 OpenGL [58] 渲染应用来实现的。

传统上，环视相机系统的成像流水线主要是为可视化而设计的。然而，这对于计算机视觉来说并非最优，因此 [59] 和 [60] 中提出了双图像流水线的概念。图像流水线的控制回路部分（如自动曝光和自动增益控制）通常是针对可视化进行调整的，因为它们无法联合调整。由于四个环视相机指向四个不同方向，它们可能处于不同的环境光照条件下。例如，阳光可能直射在车辆前部，相应的图像就会有很强的眩光和较高的饱和度；而车尾的相机则处于阴影中，画面较暗。为提高视觉质量，在将图像拼接在一起时会对图像的亮度和颜色进行协调统一 [61]。如果这种协调统一是在用于可视化和计算机视觉的通用图像流水线中进行的，就可能会对计算机视觉产生影响。