用于高性能自动驾驶的神经网络车辆模型

编者按：该论文研究了自动驾驶车辆在各种条件下的轨迹跟踪控制问题，提出结合简单物理模型的前馈-反馈控制结构，在极限工况下能够达到甚至超过人类驾驶员的性能。尽管基于物理的模型具有优势，但在实际应用中，常常无法充分利用自动驾驶车辆在行驶过程中积累的大量数据。为此，研究者提出了一种神经网络结构，通过物理模型驱动的历史状态量和输入序列进行建模，且在实验中表现优于传统物理模型。更为重要的是，当使用混合路面数据训练时，该神经网络能够无须显式估计路面摩擦系数，准确预测路面情况。这些结果为神经网络在自动驾驶车辆基于模型控制中的应用提供了新思路，具有进一步研究的潜力。

本文译自：

《Neural network vehicle models for high-performance automated driving》

文章来源：

Science Robotics, 2019,4(28):eaaw1975.

作者：

Nathan A. Spielberg, Matthew Brown, Nitin R. Kapania, John C. Kegelman, J. Christian Gerdes

作者单位：

斯坦福大学机械工程系

原文链接：

https://www.science.org/doi/10.1126/scirobotics.aaw1975

摘要：自动驾驶车辆在行驶时，首先规划并遵循一条安全的轨迹。为了确保它们的安全性优于人类驾驶员，它们必须在各种条件和关键场景下达到或超过人类驾驶员的水平。研究表明，结合简单物理模型的前馈-反馈控制结构，可以用于极限工况下的轨迹跟踪，性能甚至可以与业余冠军赛车手媲美，其关键在于拥有合适的车辆模型。尽管基于物理的模型在透明性和直观性上具有优势，但它们通常需要在特定操作点附近进行显式建模，且无法充分利用自动驾驶车辆在行驶过程中积累的大量数据。为了解决这些问题，研究者提出了一种神经网络结构，利用物理模型驱动的过去的状态量和输入量序列来进行建模。在实验车辆上采用相同的前馈-反馈控制结构时，神经网络的表现优于传统物理模型。更为重要的是，当使用来自干燥路面和雪地的混合数据进行训练时，该神经网络能够正确预测车辆行驶的路面情况，而无需显式估计路面摩擦系数。这些结果表明，该神经网络结构作为自动驾驶车辆基于模型控制的基础，具有进一步研究的潜力。

Ⅰ引言 

自动驾驶车辆有望彻底改变人类的出行方式和车辆安全性。这一前景源自其能够消除对人类驾驶员的依赖，显著降低出行成本，并在理想情况下消除94%因人类识别、决策或操作失误导致的交通事故[1]。然而，要实现这一目标，自动驾驶车辆必须能够在各种环境下，尤其是在极端条件下，比人类驾驶员更熟练地进行操纵。为此，许多自动驾驶系统采用了一个通用架构，其中上层规划层负责生成安全的无碰撞轨迹，而下层控制器则负责跟踪这些轨迹[2-5]。因此，安全行驶不仅要求生成无碰撞的轨迹，还需要控制系统能够高精度地跟踪目标轨迹，理想情况下精度达到几厘米。随着自动驾驶车辆应用范围的扩大，这些轨迹跟踪控制器必须能够应对多种路况，包括低摩擦条件下，如冰雪路面上的安全行驶，或在紧急情况下进行避障操作。所有这些情况都源自日常驾驶，特别是在车辆极限条件下，操作的精确性变得至关重要。

尽管在开发自动驾驶控制技术方面已有大量研究，但大多数工作集中在如何控制车辆在正常驾驶条件下进行温和操控，通常是在高摩擦、干燥的路面上进行[6,7]。针对车辆在接近摩擦极限时的控制研究揭示了许多挑战[8-11]。根本问题在于，当车辆接近轮胎与路面之间的摩擦极限时，车辆可能会变得不稳定（若后轮达到摩擦极限），或完全失控（若前轮达到极限）。要在这些极限条件下精确跟踪路径，就需要对轮胎与路面之间的摩擦系数进行估算，以便进行轨迹设计并发出合适的转向指令。获取这一估计通常十分困难，且由于摩擦力在不同路面条件下波动，问题变得更加复杂。除了这一关键参数的估算难度，开发一个在极限条件下依然有效的动态模型同样充满挑战，因为此时车辆的运动方程呈现高度非线性。设计者还需要在保持模型准确度与可操作性之间做出权衡，考虑是否需要包括诸如加速引起的重量转移或快速转向下轮胎力生成的滞后效应等因素。

 对于控制系统设计者而言，操控车辆至极限状态是一大挑战，但对于普通驾驶员来说，这种情况更具挑战性，并且是许多事故的主要因素。尽管如此，经验丰富的驾驶员，特别是那些有赛车经验的驾驶员，即便是业余水平，也能在车辆的极限性能下安全驾驶[13]。在赛车中，这种能力表现在低且一致的圈速上；而在关键操控时，这种能力则表现为能够在极限条件下充分利用轮胎与路面的摩擦力，以避免碰撞。如果我们希望自动驾驶车辆在关键时刻的操控超过经验丰富的驾驶员，那么对控制器的性能要求非常高。 

本文提出，采用简单的路径跟踪架构可以使自动驾驶车辆在利用轮胎与路面摩擦力方面，达到与业余赛车冠军相同的路径跟踪能力。关键在于选择合适的模型。通过使用基于物理的动力学模型进行前馈控制、简单的线性反馈控制器，并根据车辆模型的摩擦极限设计轨迹，车辆能够在摩擦极限条件下，保持低于40厘米的平均路径跟踪误差。由于模型本身仅是对实际极限的估计，我们将自动驾驶车辆的性能与业余赛车冠军进行了基准测试，比较了赛道中不同段落的圈速。通过这一新的对比方式，我们发现，在摩擦极限下操作的控制器与经验丰富的赛车手在实际道路中利用摩擦的能力相当。 

为了实现这一性能，基于物理的简单模型必须在干燥且高摩擦的赛道条件下进行精确建模。那么，如何为道路上的自动驾驶车辆开发具有可比性的模型，便成了一个关键问题。虽然获取不同车辆的参数作为开发过程的一部分是可行的，但随着道路条件的变化，一些关键参数会发生剧烈变化[14-16]。虽然已有研究提出了可以适应不同道路条件的在线参数估计技术，但这些技术尚未成熟到可以在实际汽车中商用，或满足安全关键系统的要求。此外，实时估计并未有效利用当前车辆生成的大量数据，且未来的自动驾驶车辆可能会共享这些数据。它也未能解决模型保真度问题，因为随着模型复杂度的提高，参数估算变得更加困难。理想情况下，模型生成过程应该能够利用不同摩擦条件下的数据，减少先验建模的复杂性，同时保持基于物理的模型在特定条件下的准确性和性能。 

这些挑战促使我们研究用于车辆控制的神经网络模型。神经网络因其强大的函数逼近能力，在图像识别和围棋等领域取得了显著成就[17-19]。早期的研究表明，神经网络能够用于车辆控制和动态建模[20,21]。神经网络模型在从四旋翼飞行器控制到小型拉力赛车控制的多种机器人应用中取得了成功[22,23]。虽然这些模型在车辆动态识别中取得了一定进展，但尚未应用于捕捉在多种摩擦表面上极限驾驶时车辆动态的变化[24,25]。此外，神经网络还能够利用历史信息捕捉时变效应或高阶动态行为，正如在直升机和机器人控制中的应用所示[26-28]。 

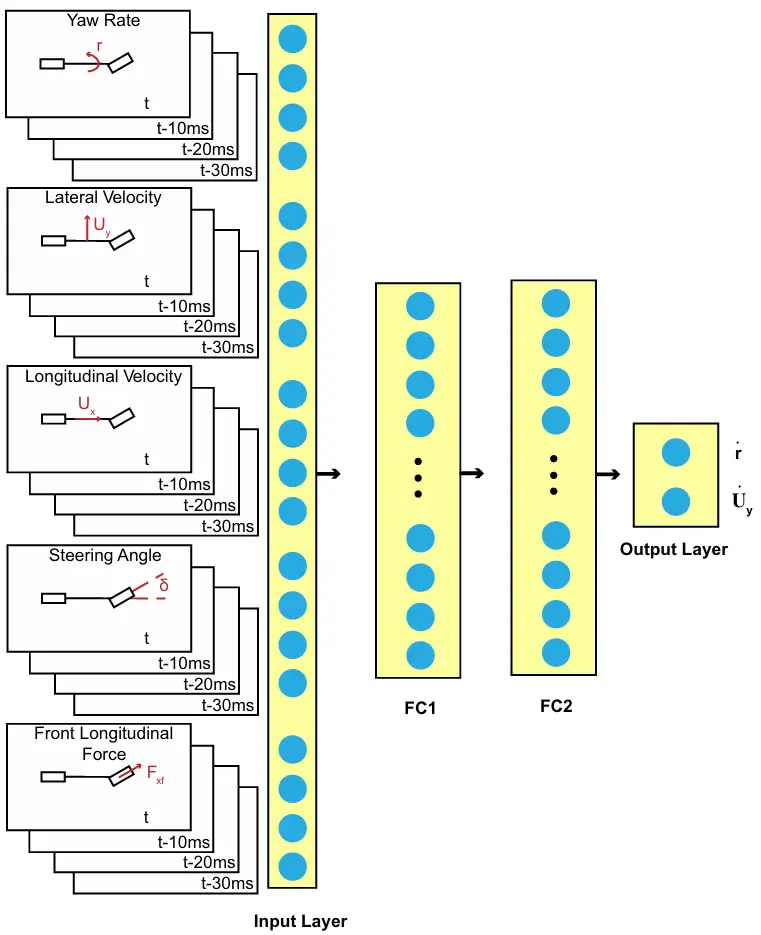
为验证这一方向的可行性，我们开发了一种两层前馈神经网络，该网络能够学习在不同路面条件下的车辆动态行为，且其输入包括来自前三个时间步的历史信息。通过这些历史数据，神经网络可以在不同摩擦水平下预测车辆的动态行为，而无需明确估算摩擦系数。当使用来自高摩擦和低摩擦路面的数据进行训练时，网络能够根据历史信息有效预测不同表面的动态行为。通过省略摩擦估计步骤，神经网络模型融合了预测和估算能力，简化了车辆控制任务，而不损失性能。仿真结果表明，与调整后的基于物理的模型相比，神经网络在极限条件下的路径跟踪性能显著提高。此外，仿真研究还验证了神经网络能够捕捉基于物理模型中未能包含的多种动态行为。

Ⅱ 结果

为了研究车辆在极限操控条件下的路径跟踪性能，我们设计了一个与经验丰富的赛车手的对比实验。在该实验中，自动驾驶车辆的合适基准是一个熟练的人类驾驶员，他不仅具有丰富的驾驶经验，还拥有业余赛车经验，并且对测试赛道非常熟悉。在实验中，我们使用了一个基于物理的前馈-反馈控制器（如图1所示）[29]，该控制器被应用于一辆自动化改装的2009年奥迪TTS（Shelley）（图2A）。该控制器的任务是跟踪预设路径，同时另一个控制器通过调整刹车、油门和换挡指令来控制车速，以达到期望的速度。路径和速度剖面通过优化方法设计，以基于车辆模型最小化完成赛道的时间[30]。

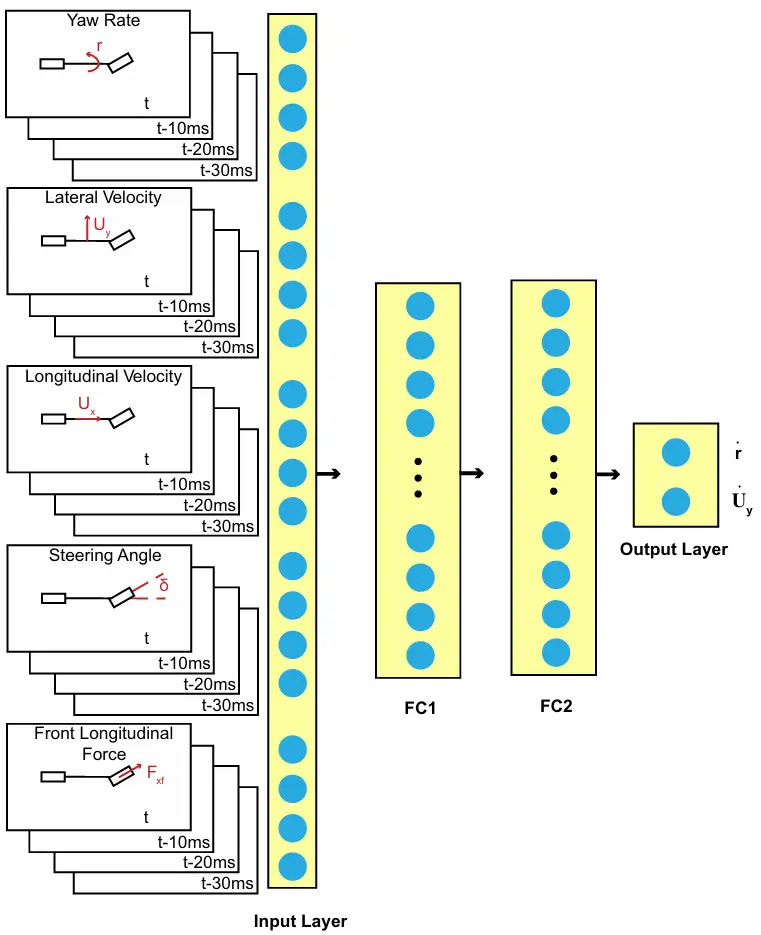
图1 用于自动驾驶汽车路径跟踪的简单前馈反馈控制结构。用于生成前馈转向命令的模型包括基于物理的模型和神经网络模型。

用于反馈-前馈控制的模型生成适当的转向角度，具体取决于给定的路径曲率和车辆的纵向速度。输入的准确性对路径跟踪误差和所需反馈控制量有着重要影响。前馈转向指令是从平面单轨或“自行车”模型的运动方程中推导而来，这是车辆动力学领域常用的模型，也是通过牛顿定律推导而得的。在本文中，所谓的“基于物理的模型”特指平面自行车模型。为了从这些运动方程计算前馈转向输入，我们假设车辆在稳态运行条件下，从而推导出所需的前馈轮胎力。这些稳态轮胎力随后通过基于物理的轮胎模型转换为转向输入，该模型明确考虑了轮胎力生成与饱和效应的影响。为了补偿前馈命令的潜在不准确性和外界干扰，我们使用了一个简单的基于路径的转向反馈控制器来精准跟踪期望轨迹。该反馈控制器通过车辆与期望轨迹之间的横向偏差和航向偏差来进行调整，如图1所示。基于物理的模型的轮胎参数是通过对实验车辆数据进行非线性最小二乘拟合得到的。 

为了将自动化控制方法与经验丰富的驾驶员的表现进行比较，我们设计了一个封闭赛道的赛车性能测试，选取了加利福尼亚州威尔洛斯的雷霆山赛车公园前五个弯道作为测试场地。自动驾驶车辆和人类驾驶员都试图以最短时间完成赛道。这一过程中，车辆需要在接近0.95g的加速度下行驶，同时在轮胎附着力的物理极限下，精准跟踪最短时间的赛车轨迹。在这种纵向和横向加速度的组合条件下，车辆能够在赛道部分区域达到95英里每小时（mph）的速度。自动驾驶车辆和人类驾驶员分别进行了10次围绕封闭赛道的驾驶实验。测试在相同的条件下进行，包括对车辆进行配重，以确保自动驾驶和人类驾驶测试中车辆的质量相等。即便在这些极限驾驶条件下，控制器依然能够稳定地跟踪赛车线路，整个赛道的平均路径跟踪误差始终低于40厘米（图2D）。

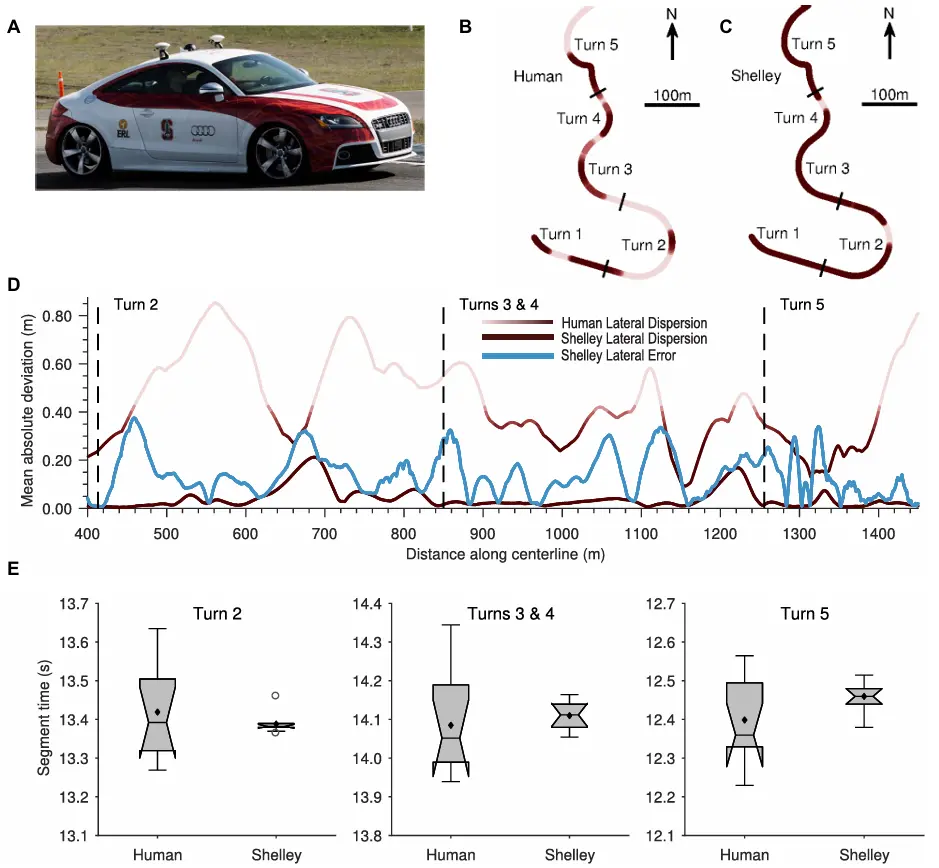
图2. 自动驾驶和人工驾驶。(A) “Shelley”，斯坦福大学的自动驾驶奥迪TTS旨在以车辆极限操纵能力进行赛车。(B)人类驾驶员的MAD中间路径投影到加利福尼亚州威尔洛斯的雷霆山赛车公园的前五个转弯处。(C)Shelley的MAD 中位数路径缩放了4倍以突出相对差异。(D)人类驾驶员和Shelley的MA 中位路径（红色）以及Shelley与预期路径的平均绝对偏差（蓝色）。(E)以Shelley为基准的业余冠军赛车手的分段时间。

为了研究路径跟踪的一致性，我们使用了中位数的平均绝对偏差（MAD median）路径分散度，这是一种衡量每次驾驶轨迹偏离赛道中心线的稳健指标。实验结果显示，经验丰富的驾驶员在各圈之间的平均路径分散度明显大于自动驾驶车辆（图2D）。这些数据也以投影形式展示在图2（B和C）的赛道地图上，其中表示测试赛道的北方方向。控制器的路径偏差一致性表明，所采用的控制方法不仅准确，而且精确。自动驾驶车辆较低的路径分散度归因于其使用高精度的基于GPS的定位系统来跟踪预计算的轨迹。正如后文所讨论的，较高的路径分散度表明人类驾驶员采用了与自动驾驶车辆不同的策略。因此，虽然人类和自动驾驶车辆的跟踪精度和变异性难以直接比较，但它们可以在时间方面进行对比。

图3 神经网络动力学模型，具有基于物理模型的输入设计。FC1 和 FC2 表示我们的两层前馈神经网络动力学模型中的全连接层。

为了比较自动驾驶车辆和人类驾驶员的表现，我们使用了分段时间这一指标，这是赛车手和自动驾驶车辆都试图最小化的目标。为了进行比较，我们将赛道分为三个部分。图2E展示了在雷霆山赛车公园进行的联合试验中记录的分段时间，涵盖了人类驾驶员和自动驾驶车辆的表现。正如带缺口的箱线图所示，Shelley在赛道每个部分的用时均落在熟练人类驾驶员的分段时间范围内，这表明基于模型的控制器在车辆能力极限下的表现与经验丰富的赛车手相当。在每个箱体上，中位线代表中位数，黑色菱形标记表示平均值，箱体的边缘为第25和第75百分位数，须线延伸至不超过四分位距（IQR）1.5倍的相邻样本之外，超出部分被标为“异常值”。缺口部分提供了一个视觉对比区间，计算为中位数。圈速相当的结果表明，简单的前馈-反馈控制器与其基于物理的模型具有相当的摩擦利用能力。与人类驾驶员相比，低路径分散度和相当的分段时间是基于针对特定路面调整的模型的结果。在与经验丰富的驾驶员的性能对比基准建立后，我们可以将这种控制器的性能作为神经网络模型的参考基准。

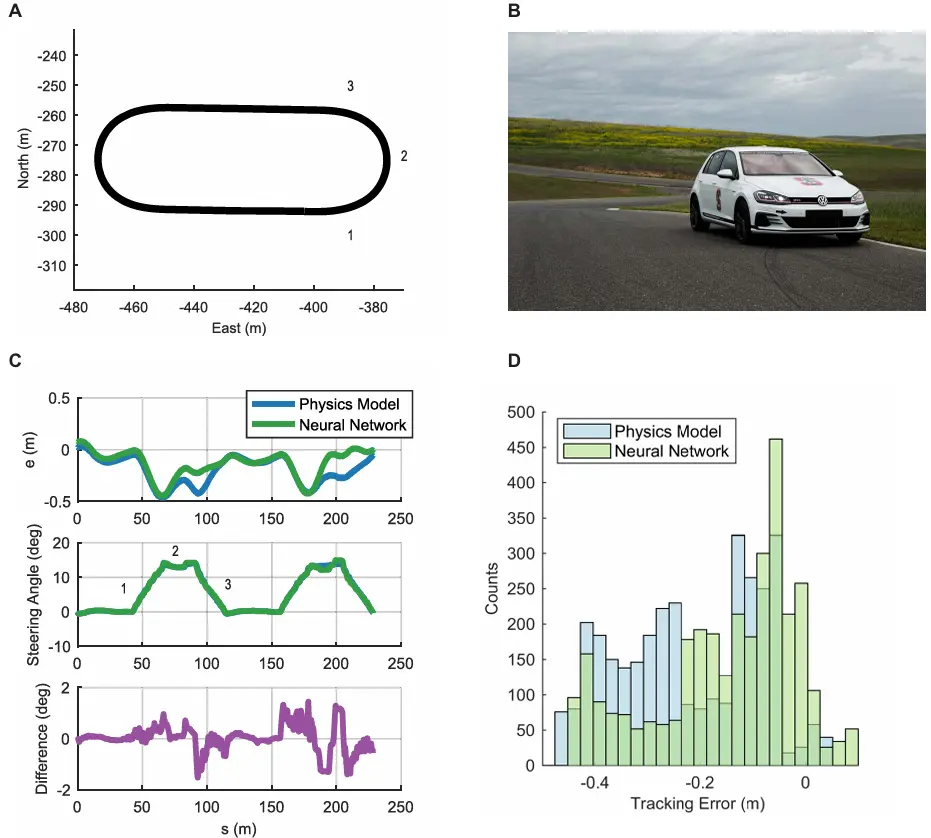
图4 实验模型比较。(A)实验轨迹图，在实验数据图中显示相应的第1、2和3部分。(B)大众GTI实验性自动驾驶赛车的图片。(C)基于物理的控制器和神经网络控制器之间的实验比较显示，在椭圆形测试轨道的限制下跟踪误差较低。(D)直方图显示椭圆形测试跑道上神经网络和基于物理的控制器的横向误差分布的差异。

受到基于物理模型中状态和控制启发的影响，我们选择使用图3所示的前馈神经网络作为输入。该神经网络模型包含两个隐藏层，每层128个单元，并且每个状态或控制输入都使用三个延迟输入状态。与基于物理的模型相似，该网络能够预测车辆的偏航率和侧向速度的导数。该网络最初通过监督学习的方式进行训练，旨在复制基于物理的模型。在基于物理模型的输入空间范围内，我们使用200,000条轨迹进行训练，并使用从高摩擦和低摩擦测试中收集的实验车辆数据来更新神经网络。高摩擦测试在雷霆山赛车公园进行，低摩擦测试则是在北极圈附近的冰雪混合跑道上进行。

虽然神经网络模型可以应用于各种控制方案，但我们希望将其与基于物理的前馈-反馈控制器提供的基准进行比较。因此，我们使用训练好的神经网络模型生成前馈指令，假设与基于物理的模型相同的稳态条件。为了生成前馈转向命令，我们利用二阶非线性优化方法，求解神经网络动力学模型的平衡点。测量的速度和路径曲率作为优化的输入，来指定正确的前馈命令。该优化过程在线进行，每秒20次，从神经网络中计算前馈转向命令。为了补偿干扰和模型失配，我们在两种控制方案中都使用了相同的基于路径的简单反馈控制器结构进行控制器之间的比较。

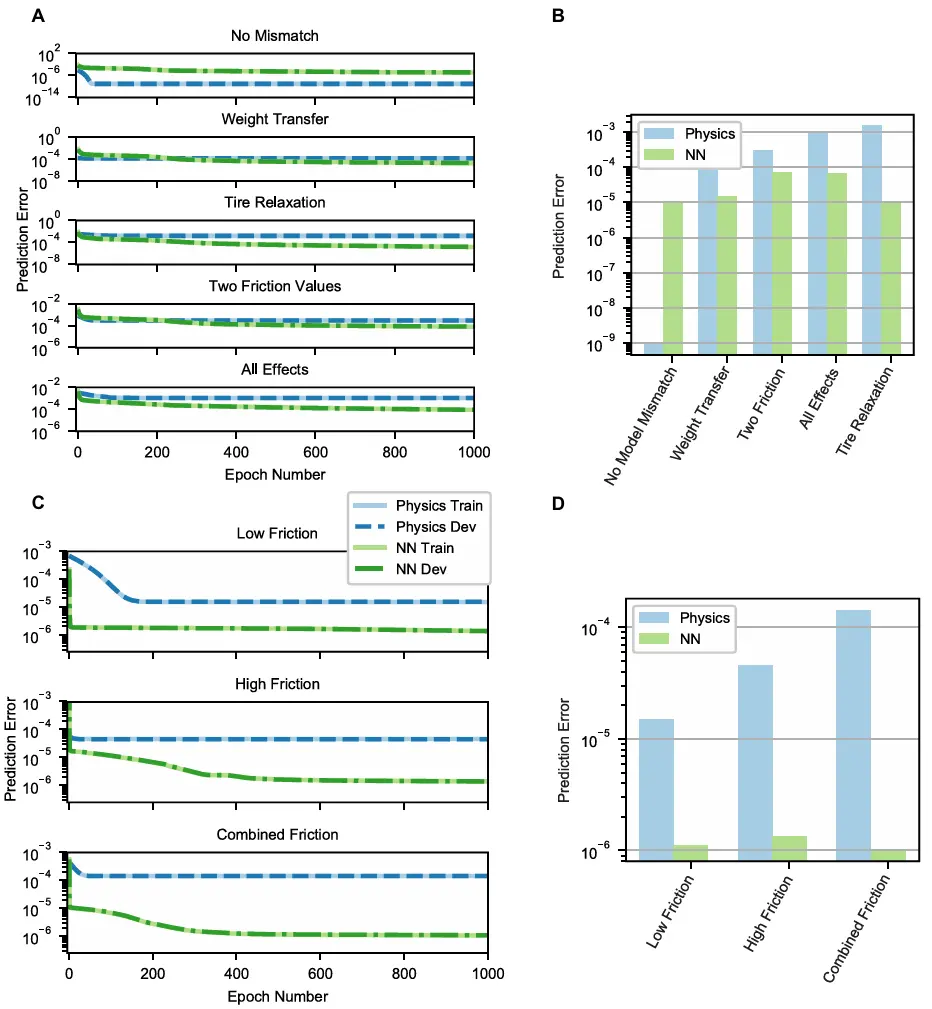
图 5.训练和测试。(A)模拟数据的训练过程，包括数据生成和优化模型之间模型不匹配的多重影响。(B)模拟数据的测试过程，显示学习模型的泛化能力。(C)在各种摩擦条件下对真实采集的车辆数据的训练过程。(D)显示学习模型的泛化能力的真实车辆数据的测试过程。

我们通过在一辆自动驾驶的大众GTI（图4B）上实施这两种控制器进行比较，并利用这辆具有自动驾驶功能的车获取雪地数据。图4A展示了在雷霆山赛车公园的滑行垫上用于评估这两种控制器的椭圆形赛道。两种控制方案使用相同的纵向速度剖面和纵向控制器，并在车辆能力的极限下进行了测试。比较结果表明，在转弯入口处（图4C中标记为“1”），神经网络控制器相较于基于物理的模型，学会了更多的转向量，从而在转弯中间的跟踪误差更低。在转弯中，跟踪误差受到可用路面-轮胎摩擦力的影响，负误差表示车辆超出了抓地力极限。此外，由于更接近期望路径，神经网络控制器在转弯出口处（“3”）命令的转向较少。图中显示的出口和直道部分的峰值则受转向反馈参数的影响，例如控制器增益和前瞻距离。我们发现，神经网络控制器在极限条件下，能够显著改变一圈内侧向误差的分布（图4D）。该分布显示的计数是基于2.4厘米的箱体大小，所选的箱体数量为25。上述结果表明，在相同稳态假设和控制架构下，神经网络模型能够提供比基于物理模型更高的模型保真度，满足该赛道的期望性能基准。 

数据驱动模型的真正优势不仅在于提供与基于物理方法相当的性能。神经网络模型还具有整合更高阶动态效应的潜力，并能够学习不同路面条件下的车辆行为。为了验证我们的学习模型（图3）是否具备这些特性，我们在两项额外的研究中检验了其预测能力，这些研究结合了更高保真度的车辆动力学建模以及多个路面摩擦值。

 为了展示神经网络相对于简化物理模型的建模能力，我们使用不同保真度的动态模型基于均匀随机控制策略生成训练数据。这些数据不仅用于训练网络，还用于识别基于物理模型的最佳拟合参数，以便进行比较。在第一次比较中，物理模型本身生成了数据，因此模拟数据的物理模型与学习到的物理模型之间不存在模型失配。在这种情况下，图5A中的“无失配”结果显示，基于物理的模型显著优于神经网络模型，并恢复了用于模拟的参数集。这是可以理解的，因为基于物理的模型代表了数据背后的真实模型形式，而神经网络则尝试学习一个近似模型。 

然而，当不同保真度的模型生成训练数据时，情况发生了变化。我们使用经过增强的基于物理的模型生成了模拟数据，这些模型考虑了纵向重量转移、轮胎松弛长度以及多个路面摩擦值的影响（图5A）。当这些数据拟合到简单的基于物理的模型时，额外的模型失配效应导致了有偏的参数值。我们发现，在所有这些模型失配的情况下，神经网络模型在预测方面优于基于物理的模型（图5A）。此外，我们还发现这些结果可以扩展到保留的模拟数据（图5B）。这些结果与用于设计神经网络预测模型的物理见解一致。例如，在学习轮胎松弛效应时，神经网络能够通过包括多个延迟阶段的状态和输入来捕捉变化的滑移角动态，而基于物理的模型仅使用当前输入和状态来预测车辆的动力学。 

受到神经网络在模拟中捕捉丰富动态能力的启发，我们设计了另一项研究，以评估模型在现实条件下对不同路面预测的能力。为此，我们使用大众GTI平台（图4B）收集了手动驾驶和自动驾驶的数据。此外，我们还收集了在干燥沥青上的高摩擦驾驶数据，以及在雪地和冰面上的低摩擦驾驶数据。为了验证神经网络在低摩擦和高摩擦条件下学习动态模型的能力，我们分别对每种条件单独进行了训练和验证（图5C）。结果表明，无论是在高摩擦还是低摩擦情况下，神经网络结构都优于基于物理的模型。这两种条件的数据还可以进一步结合，用于训练单一神经网络或基于物理的模型。我们发现，由于基于物理的模型无法捕捉这两种不同摩擦条件的变化，导致其训练和测试误差最高（图5C）。识别出的基于物理的模型特征大致代表了平均路面条件，而神经网络模型的隐藏节点能够隐式表示和应用不同的路面条件。因此，神经网络在训练和测试中都优于基于物理的模型一个数量级以上。更重要的是，这些结果表明，神经网络模型在混合和孤立的路面数据上均表现出更好的预测性能，这一特性也适用于保留的测试数据（图5D）。

Ⅲ 讨论

结果表明，有了合适的模型，简单的前馈-反馈控制器可以在车辆摩擦能力的极限下提供路径跟踪性能，其摩擦利用与经验丰富的赛车手相当。此外，我们的可行性研究证明，神经网络可以为这种方法提供必要的模型，其性能优于简单但精心调整的静态基于物理的模型。最值得注意的是，这种模型可以在不明确识别摩擦的情况下预测不同摩擦表面的性能，并在考虑更高保真度的车辆动力学特性时表现出鲁棒性。这里展示的测试表明，这样的神经网络结构是自动驾驶车辆动态模型的可行候选，并值得进一步研究。 

将本文介绍的路径跟踪控制器与人类驾驶员的表现进行基准测试是充满挑战的。正如路径分散度所示，人类驾驶员并非精确地进行路径跟踪。相反，他们通常倾向于在某些关键点，例如弯道顶点，锚定期望路径，并专注于将车辆推向摩擦极限。由于人类驾驶员的方法与典型的自动驾驶架构截然不同，分段时间成为两者比较的一个更公平的标准。无论是人类驾驶员还是期望轨迹，二者的目标都是最小化行驶时间。鉴于分段时间对摩擦利用的极端敏感性，合理的分段时间可以推断出相当的摩擦利用程度。 

此外，尽管我们的冠军业余赛车手表现出色，但专业赛车手的速度更快，表明他们具备更强的摩擦力利用能力。因此，虽然我们展示了与经验丰富的赛车手相当的表现，但尚未展示出超越人类表现的高端能力。要实现这一点，可能需要采用赛车手更倾向于偏离路径，以更充分地利用摩擦力和减少时间的策略。 

比较神经网络模型与基于物理模型控制性能的结果显示，神经网络控制器在选定的测试路径上具有更优的路径跟踪性能。基于物理模型的控制器在转弯时出现较大的侧向误差，接近50厘米。然而，考虑到典型车道宽度在2.7到3.6米之间，车辆宽度为2米，两种控制器即便在摩擦极限下也能保持车辆在车道边界内（31）。在测试路径上，转弯速度未超过26英里每小时，因此该实验反映了城市或郊区驾驶中紧急操作的合理模型。尽管部署前还需要通过其他操作进行验证，但这些结果证明了神经网络方法在极限条件下进行车辆控制的可行性。 

当使用神经网络模型时，控制器的前馈计算仅依赖于模型状态空间的一部分（车辆处于稳态）。然而，神经网络具有学习瞬态动态效应的能力，这一点通过其一步预测误差得到了体现。因此，在这种特定的控制架构下，神经网络在控制方面的真正潜力尚未完全发挥。此外，由于前馈控制器仅在稳态假设下生成命令，网络的状态历史受到限制。当前的前馈控制器未能充分利用神经网络同时估计和预测可变摩擦表面特性的能力。其他控制结构，如模型预测控制，可以充分利用网络的估计能力，提供将估计和控制结合的简单方法。另一个选择是使用更复杂的物理模型或在线估计参数。然而，这一系列比较为建立神经网络模型的质量提供了一个清晰的基准，相较于传统方法和人类表现。 

在学习车辆动态的神经网络模型时，学习过程非常高效，所需的物理车辆数据仅为35分钟。因此，收集其他路面、条件和轮胎的数据成本较低，且具备可行性。未来的研究可以进一步探讨是否能够将不同路况和条件有效编码到该神经网络结构中。

 Ⅳ 材料和方法

A. 基于物理的模型

所提出的基于物理的控制设计结构基于平面单轨模型（即自行车模型）来假设车辆动力学，如图6A所示，相关参数在表1中进行描述。平面自行车模型的核心假设是左右轮胎产生一个单一的组合侧向力，从而仅在前后轴上产生两个侧向力，分别为和。施加在前轮胎上的转向角会引起通过滑移角和产生的侧向轮胎力。由此产生的两个关键状态是车辆的偏航率（描述车辆的角旋转）和侧滑角（即侧向速度与纵向速度的比值）。鉴于我们主要关注车辆的横向控制，纵向速度被视为时变参数，而不作为车辆状态的一部分。

表1. 物理模型定义

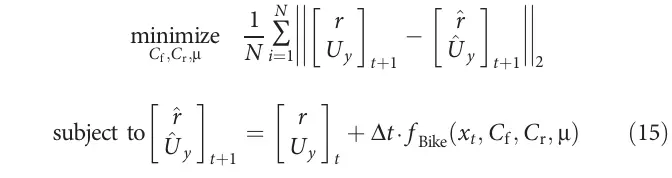
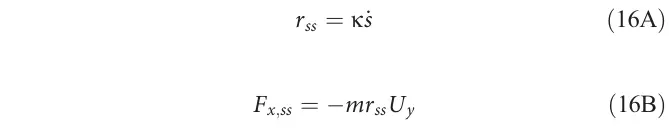
图6 .基于物理的模型和轮胎模型。(A)平面自行车模型示意图，包括误差状态，在本文中称为基于物理的模型。(B)前后轮胎曲线，使用刷子 Fiala 模型拟合经验轮胎数据。

除了两个车辆状态和之外，还需要两个额外的状态来描述车辆相对于期望路径的位置，如图6A所示。横向路径偏差（即横向误差）表示车辆质心到期望路径上最近点的距离；而车辆航向误差则是车辆中心线与期望路径切线之间的角度差。 

图6A中所示状态的运动方程由以下给出：

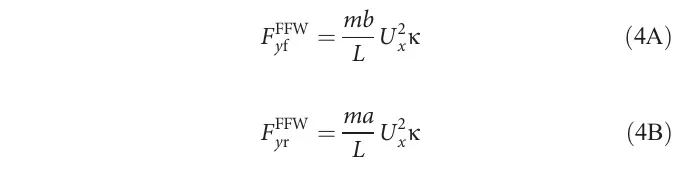
为了获得以误差状态导数表示的前馈控制器设计的运动方程，我们可以对和取时间导数，设，并从方程1A和1B中代入，得到：

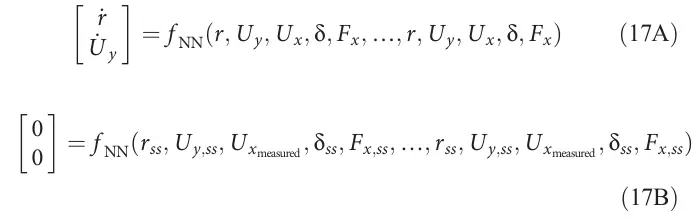
自行车模型的动力学简化为方程3B所示的形式，用于描述向量值学习自行车模型。模型中的轮胎参数（如、、）通过学习来预测，并由从实验数据中获得的车辆测量值进行估算。在时刻，输入到横向自行车模型的变量记作，如方程3A所示。

B. Lookahead 控制器

作为控制基准，基于物理的控制器采用前馈-反馈架构（如图1所示）。前馈转向角的输入为当前路径曲率和前进速度，反馈转向角的输入为误差状态和。最终的转向指令是反馈与前馈输入的加权和。

转向前馈的目标是提供一个估计的转向角，用于穿越具有已知路径曲率和速度剖面的路径。这可以最小化转向反馈所需的补偿量，减少跟踪误差。前馈转向角应仅依赖于期望的轨迹，而与实际车辆状态无关。 

为了从基于物理的模型设计前馈转向控制器，我们做出了简化假设，即车辆在稳态转弯条件下运行。此假设已被证明[32]有助于减少控制器偏航率响应的振荡。在方程2中设置和，得到以下稳态前轮和后轮的轮胎力公式：

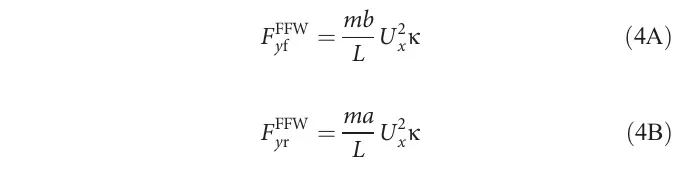
在稳态条件下，假设角度较小，车辆的前馈转向角与前轮和后轮的侧向轮胎滑移角和以及路径曲率通过车辆运动学关联。

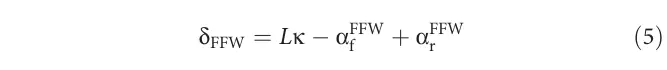
具体地，前馈转向角与前轮和后轮的综合前馈轮胎滑移角和相关。 

前馈轮胎滑移角的选择与方程4中的轮胎力通过轮胎模型相关。为了考虑轮胎力随轮胎滑移幅度增加而饱和的情况，采用单摩擦系数刷子模型[33]将侧向轮胎滑移角映射为轮胎力，具体如下：

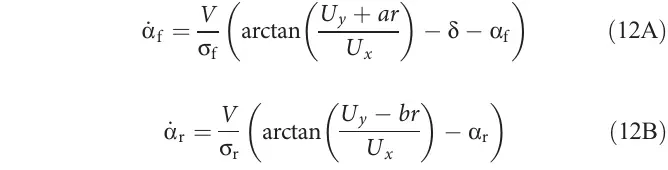
其中符号表示前轮或后轮，是路面摩擦系数，和是对应的转向刚度和法向载荷参数。转向刚度和摩擦系数是通过使用非线性最小二乘法拟合实验数据得到的，如图6B所示。 

随着前馈设计的完成，剩下的步骤是设计反馈控制器。反馈控制器的目标是最小化一个前瞻距离误差，这是车辆跟踪误差投影到车辆前方距离处的误差（图6A）。 前瞻误差和相应的反馈控制律如下所示：

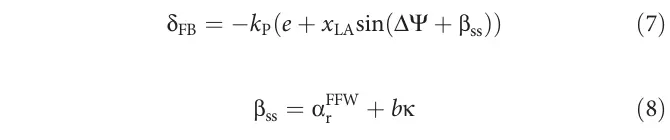
式中具有比例增益。注意这个反馈控制器的一个关键特点是包含了稳态侧滑信息。文献[32]指出，考虑反馈控制律中的侧滑信息能够消除稳态路径跟踪误差，前提是没有模型与实际情况的不匹配。此外，线性系统的分析表明，使用稳态侧滑信息，而非测量的车辆侧滑，可以使控制器在稳态下保持足够的稳定性裕度。

C. 与人类驾驶员对比

为了提供一个基准来评估基于物理的控制器，我们将Shelley的性能与一位熟练的驾驶员进行了比较。该驾驶员拥有多年的业余赛车经验，并且曾与研究团队合作。此外，这位驾驶员对赛道非常熟悉。基于物理的前瞻控制器被实现在Shelley上，这是一辆2009年的奥迪TTS。Shelley配备了主动刹车助力器、电子油门和电子助力转向系统，能够实现完全的自动驾驶控制。此外，Shelley使用了差分全球导航卫星系统（DGPS）信号辅助的集成导航系统，提供厘米级精度的位置测量。该系统包括一个dSPACE MicroAutoBoxII，用于记录车辆数据，并以200Hz的频率执行控制命令。 

为了比较基于物理的前瞻控制器与熟练驾驶员在赛车性能上的差异，我们通过比较分段时间和路径分散度来展示实验结果。实验测试在位于加利福尼亚州威尔洛斯的雷霆山赛车公园进行。人类参与者和Shelley分别进行了东赛道2至6号弯道的10次连续试验。在每次试验中，车辆的总质量保持一致。我们使用GPS标记将每次试验分割成三部分进行分析。对于两位参与者，从GPS记录的行驶路径被用来计算横向偏差和沿赛道中心线的距离。为了描述每位参与者轨迹的分散度，我们选择了中位数的平均绝对偏差（MAD median）。

D. 学习全局神经网络模型

与在基于物理的模型中学习参数不同，我们学习了一个神经网络模型，该模型能够省略建模和识别潜在状态（例如车辆与路面摩擦的相互作用）的步骤。在建模未知或变化的动力学时，设计者通常需要将所有未知或未建模的效应压缩到一个预定义维度的给定参数集中。通过使用一个既包含控制又包含状态历史的向量表示的神经网络模型，我们对系统识别任务施加了较少的结构，允许网络模型识别其自身对时变动力学的内部表示。在扩展的网络输入空间中，给定点可以用来完整地构建系统的潜在状态，前提是延迟阶段的数量足够长。这一点通过Takens定理得到了证明，并在学习复杂的直升机动力学模型中得到了进一步验证[27,34]。 

我们学习了一个形式如方程9所示的神经网络动力学模型，其中表示学习到的网络权重参数，表示每个阶段的延迟状态和控制输入，表示状态和控制输入的历史，是使用softplus激活函数的双隐藏层神经网络动力学模型的缩写。在网络方程中，表示层激活，表示给定层的加权输入。

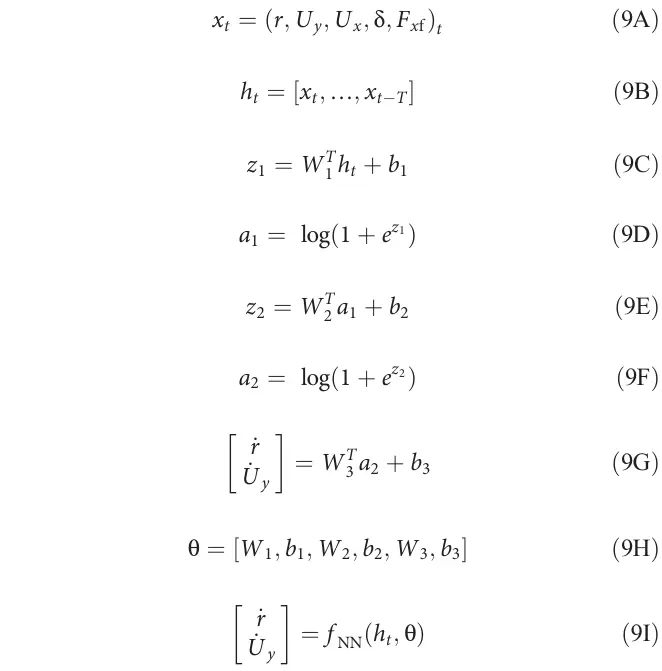
网络的训练目标是预测下一个测量的偏航率（）和侧向速度（）状态。网络的测量输入每步延迟10毫秒。为了预测目标状态，我们使用网络学习了状态导数，然后使用10毫秒的时间步长（）进行欧拉积分，如下所示。基于物理的模型的预测目标也使用10毫秒的时间步长进行欧拉积分，其中表示下一个采样时间步长。

E. 仿真数据

为了研究神经网络学习这些效应表示的能力，我们设计了一个使用基于物理模型的模拟研究，该模型具有不同程度的额外模型复杂性。为了展示神经网络模型对车辆动力学建模的能力，我们使用了之前描述的单轨车辆模型和Fiala轮胎模型。为了使用基于物理的模型生成数据集，如方程1所示，我们首先在稳定初始状态的空间中均匀随机地采样初始条件（）。我们还在可能的输入空间中均匀随机地采样初始控制（）。为了创建一个长度为的单一轨迹，用作网络训练的输入，我们使用了均匀随机控制策略，对于,，使用基于物理模型的动力学来确定剩余控制轨迹的下一个状态。除了使用高摩擦的基于物理的模型生成训练数据外，我们还模拟了以下额外的动态效应。

F. 载荷转移

在高性能驾驶中，影响车辆动力学的一个常见效应是纵向载荷转移。该效应通过增加或减少每个轮胎所经历的法向力，进而影响车辆的动力学，通常是由于加速或制动所导致。方程11显示了载荷转移的影响，其中是车辆质心的高度，是车辆质量，是重力加速度。与Fiala轮胎模型结合时，纵向载荷转移会导致给定轮胎的力能力增加或减少。我们采用一个包含基于物理的模型，并结合纵向载荷转移效应的动力学模型，生成了一个模拟数据集。

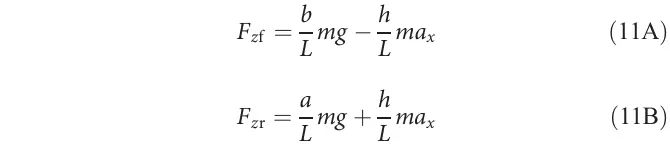
E. 轮胎松弛

在低速驾驶中，另一个需要建模的主要效应是轮胎松弛长度。轮胎松弛长度可以被建模为每个轮胎所经历的侧向力的延迟，如下方程12[35]所示。延迟的量由轮胎松弛长度决定，这是轮胎的一个属性，以及车辆速度的大小。我们使用一个包含轮胎松弛长度效应的基于物理的模型生成了一个模拟数据集。

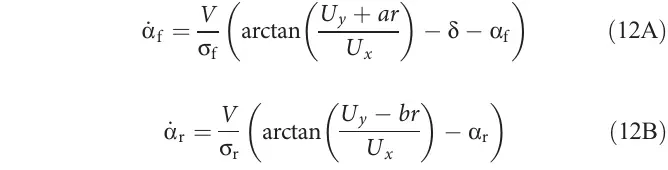
G. 摩擦力验证

为了验证神经网络模型在多种环境条件下具有高预测性能的能力，我们生成了一个包含高摩擦和低摩擦数据的模拟数据集。通过在Fiala轮胎模型的摩擦参数中明确建模高摩擦和低摩擦表面，我们生成了数据集，其中高摩擦和低摩擦表面的摩擦值分别如方程13所示。这个数据集包含了200,000条采样轨迹用于训练，其中一半数据是在高摩擦条件下收集的，另一半则是在低摩擦条件下收集的。

最终，我们将所有这些效应合并到一个基于物理的模型中，生成了一个包含200,000个样本的模拟数据集，用于训练神经网络模型。

H. 实验数据

为了展示神经网络模型在真实预测测试中的能力，我们在高摩擦和低摩擦驾驶条件下收集了车辆数据。所收集的数据涵盖了模拟中展示的所有建模效应，包括高摩擦和低摩擦情况，以及一些难以建模的效应，如悬挂几何形状和内部控制回路。总共有214,629个轨迹样本，约35分钟的驾驶数据，数据大致均匀分布在高摩擦和低摩擦驾驶之间。这些数据是通过使用类似于Shelley平台的自动化大众GTI车辆收集的。低摩擦数据是在北极圈附近的测试跑道上收集的，覆盖了不同速度范围，直到车辆在低摩擦测试跑道上的极限。高摩擦数据则是在雷霆山赛车公园收集的，涉及各种操作的极限数据。 

一个集成导航系统被用来测量,,,，其中表示车辆的纵向加速度。车辆的转向角度测量值通过车辆控制器局域网（CAN）获得。所有数据以100Hz的频率记录在dSPACE MicroAutoBox上。在学习任务中，为了仅学习相关的车辆动力学，我们使用一个6Hz截止频率的二阶巴特沃斯低通滤波器对记录的数据进行了滤波，以避免包含高频效应，如悬挂振动。

I. 优化与训练

在准备学习数据时，每个实验数据集被分为70%用于训练，15%用于开发，15%用于模型测试。为了打破数据集内的时序相关性，我们随机化了数据，确保每个样本由一个时间相关轨迹组成，但任意两个样本之间不相关。为了比较基于物理模型和神经网络模型的能力，我们优化了这两个模型，使其能够拟合观测到的动力学训练数据。我们使用均方误差（MSE）作为训练目标，如下所示，其中和表示模型预测的量,和是测量的目标量，表示训练样本的数量。通过训练网络，我们解决了如方程14所示的优化问题，其中表示网络的权重。

为了将基于物理的模型优化到观测数据，我们同样形成了一个优化问题来训练模型参数。基于物理模型的参数包括轮胎摩擦系数()和轮胎前、后轮的转向刚度（和）。由于存在模型失配，任何观测到的模型失配都会导致模型参数的变化。同样，在从包含额外未建模效应的基于物理的模型生成的数据中，模型失配也会导致参数变化。因此，我们解决了优化问题（方程15）来训练基于物理模型以拟合记录数据。

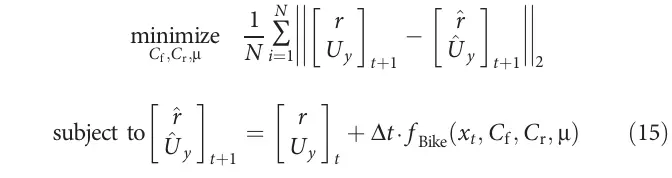
基于物理模型的参数是从随机高斯分布初始化，而神经网络模型的参数使用Xavier均匀初始化方法进行初始化。我们使用Adam优化方法，并采用默认参数初始化，执行基于物理模型和神经网络模型中学习参数的一阶优化[36]。训练过程使用每批1000个样本的迷你批次进行每次更新。学习框架是在Python中使用TensorFlow实现，并通过图形处理单元（GPU）并行化进行训练。训练使用的计算集群配备了Intel i7处理器和Nvidia 1080显卡[37]。对于单个训练数据集，整个学习过程大约需要25分钟。

J. 使用基于学习的模型进行控制

为了使用学习到的神经网络模型控制车辆，我们开发了一种基于前馈-反馈控制架构的方法。在这种方法中，学习到的神经网络模型用于生成近似的前馈转向和侧滑命令。首先，我们在来自自行车模型模拟的高摩擦数据上训练神经网络，这些数据在模型的状态空间中采样了200,000条轨迹。初步训练完成后，我们使用真实实验数据进一步训练模型，这一过程受逐步提高模型保真度模拟器技术的启发[38]。我们补充了来自高摩擦和低摩擦实验测试的真实数据，并从基于前馈-反馈控制器跟踪椭圆形测试赛道的数据中获取了额外的实验数据。将这些数据合并后，神经网络车辆模型重新训练以拟合新的真实数据，如图7所示。一旦模型在真实数据上优化完毕，它便用于生成前馈转向和侧滑命令。 

从神经网络动力学模型中未学习到的运动学来看，我们发现在稳态时，可以得到：

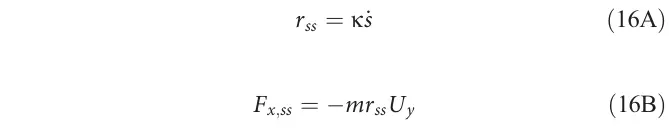
稳态值被用作优化问题的输入，以找到前馈控制的驻点。寻找驻点的条件是通过找到一个状态导数为零的点来实现。在具有历史信息的神经网络中，这意味着每个延迟的状态和控制输入被约束为相同，如方程17B所示。

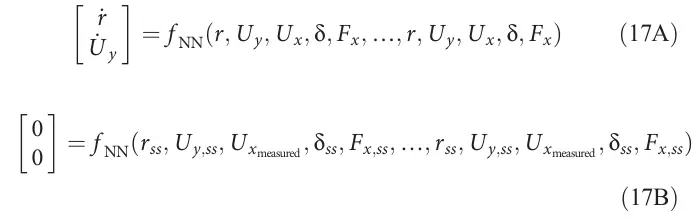
为了像基于物理的控制器那样计算前馈值，控制器需要知道速度和路径曲率。速度是车辆传感器测量并作为网络的输入，而曲率是从预计算的轨迹提供的。在实际控制过程中，曲率是通过车辆上的地图匹配算法在线计算的。 

最后，控制器计算前馈命令和，这些命令在执行限制（）内最好地实现平衡。这个解是使用约束的二阶内点优化方法优化的。这个过程使用了CasADi和IPOPT来解决如方程18所示的以下非线性优化问题[39, 40]。

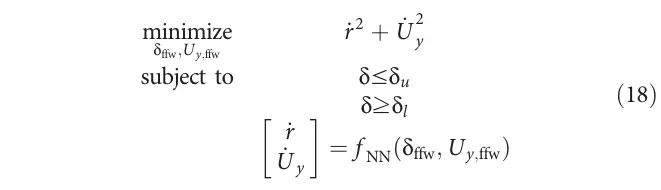
该优化问题旨在以最小二乘法的意义找到与学习模型稳态最接近的控制输入。在实践中，优化结果在车辆测试期间的最大成本函数值为。每50毫秒，优化问题将在配备Intel i7处理器的计算机上重新求解。运动学转向角被用作优化的初始猜测，尽管该问题对初始猜测并不十分敏感。 

在获得用于控制的转向值时，我们结合稳态侧向速度和当前速度来计算前馈侧滑角，如方程19A所示。一旦计算出前馈侧滑命令，它将与前馈转向命令一起，作为车道保持反馈控制方案的一部分，进行进一步的控制计算，如方程19B所示。最终的转向命令由前馈网络的驻点解和路径基反馈转向附加项共同决定。与基于物理的控制器类似，转向反馈包括前馈侧滑项，这一项基于从网络计算出的最佳稳态侧向速度解。

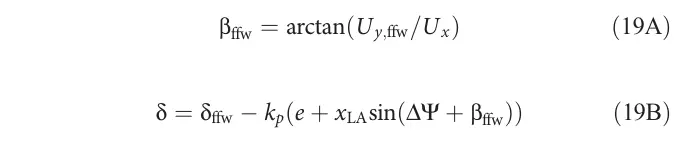
最终计算出的转向命令通过车辆的CAN接口发送，并通过一个低级转向控制器进行跟踪，后者向车辆的转向系统施加扭矩，以达到期望的车轮角度。 

基于物理的前馈控制器和神经网络前馈控制器的比较在一辆自动化的大众GTI上进行。两个控制器均在雷霆山赛车公园的沥青高摩擦滑行垫上的椭圆形测试轨道上进行了测试。实验中，两种控制器均使用了一个前馈-反馈的纵向控制器。两种控制器的跟踪误差在车辆测试期间进行了比较，数据分析在MATLAB 2016b中完成。

参考文献