某商务车制动器有限元分析

1. 引言

随着世界经济和科学技术的双重发达，人类生存的经济基础日益优越，出行用具也从最初的牛羊马转变为轿车。车辆让人类日常生活更加方便，并且已经变成了人类日常生活中十分主要的组成部分。但是，由于汽车在给人类日常生活带来方便的同时却产生了大量的和汽车有关的事故，因此车辆运行的安全性问题也越来越引起人们重视，而车辆制动系统的安全性与可靠性问题也日益受到人们的关注。车轮制动作为车辆的关键部分，其性能的优劣将直接影响车辆的行驶安全性。盘式刹车制动反应迅速、散热性佳、性能平稳，不过具有温度场分配不均衡、使用寿命短、刹车噪音大等弊端，所以盘式刹车一直是国内学术界研讨的热门话题 [1] 。

制动器主要零部件之间产生共振会导致制动噪声等不良影响 [2] 。高若奇等 [3] 人把材料的温度关系也考虑了进来，对制动盘进行了热力耦合研究，得出了制动盘的应力场和温度场结果。曾昱皓等 [4] 对某新型盘式刹车的关键构件进行了静应力研究，得出零部件最大应力，为此类制动盘的优化提供理论依据。董慧丽等人 [5] 阐述了盘式刹车时摩擦噪音的产生规律和原因。周昌祁等 [6] 研究表明通过降低工作温度、磨擦因数和制动能能够降低制动器的刹车噪音。施佳辉等人 [7] 对盘式刹车系统进行了振动噪音测试，发现改变制动器的阻尼比能过有效的避免制动盘与摩擦片之间的共振。张立军等 [8] 人对盘式刹车的接触压力和热机耦合稳定性进行了模拟研究。李志刚等 [9] 对盘式制动器进行了结构优化。

论文内容以某商务车圆盘制动系统为主要研究对象，先通过UG构建盘型制动主体零件的三维建模，然后将文件另存为STP格式并引导到HyperMesh软件中，进行有限元模态的解析。因为1~6阶模态都是刚体运动模态，所以频率几乎为0，故将仿真的第七阶模态作为第一阶模态来处理。详细分析了制动盘跟摩擦片的前六阶模态，对降低刹车过程中产生的振动和结构优化问题进行了理论指导。

2. 有限元模态分析理论

模态分析主要是把系统振动微分方程组中的各带有线性时不变特征的物理坐标转变为模态坐标系，进而解耦微分方程，并由此接触一个独立方程组，而该方程组则以模态坐标系和模态函数表示，则经过模态坐标系转变后所获得的矩阵便是体系模式振型矩阵，则此矩阵中的所列矢量即为相应的体系各阶段模式振型，把这种程序描述为体系模态分析。对结构力进行模态分析就可获取了整个体系的模态参数，进而确定了整个体系的模态参数，还可以对整个体系的有关振动问题做出了提前预测和规避，从而减少了不必要的因震动所造成的结构破坏和故障，并且还能够为结构力特性的改善提出更强大的理论数据支持。模态分析方法主要是用来判断结构的振动特征，如固有频率和振型等，这对于避开共振十分有用，是结构动态载荷设计的关键参数，同时也是光谱分析、谐响分析、暂态动力学分析等动力学分析方法的基石。每一种模态都有特殊的固有频率和模态振型。在本文中模态分析的各阶段固有频率理论，其自由振动方程为

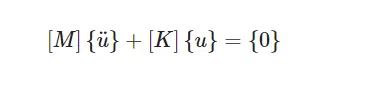
式中：

[K]是刚度矩阵；

[M]是质量矩阵；

{u¨} 和 {u}是加速度向量和位移向量。

求解自由振动方程可得出的频率代数方程式，如式

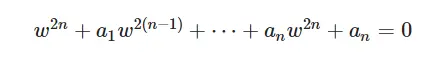
将以上方程求解之后便可得到各阶的固有频率跟振型。

3. 盘式制动器建模

3.1. 盘式制动器的三维建模

制动盘、摩擦片、刹车卡钳、制动钳固定支架、制动油管和复位簧片是盘式制动器的主要零部件。我们取消了一些基础的构造、省略了小孔径的螺纹连接，只对制动盘和刹车摩擦片进行了研究，以此来优化盘式制动器的实体模拟，从而增强了有限元的正确性以及计算速度。并在UG中建立了制动盘与摩擦片的三维建模，如图1所示。

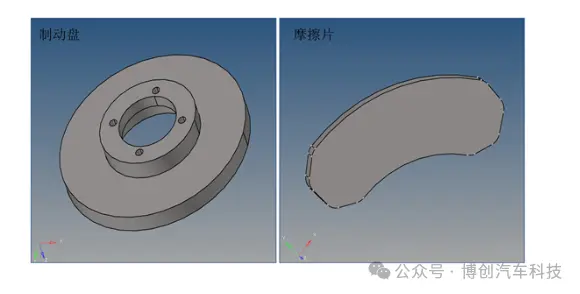图1. 制动器零部件三维模型

3.2. 盘式制动器的有限元模型

将零部件的三维模型导入到HyperMesh软件中进行有限元模态分析。

1) 定义材质属性：盘式制动器零部件的材质参数如表1所示。

表1. 盘式制动器零部件的材料参数

2) 规划网格：网格规划的品质和密度对有限元分析的研究结果有着十分重大的关系，而网格的品质又直接关系最后的研究结论，所以我们采用六面体单元类型来划分网格，如图2所示。

图2. 制动器零部件网格图

3) 将模态分析确定为分析类型。本文采用的模态分析为自由模态。

因为1~6阶模态都是刚体运动模态，所以频率几乎为0，故将仿真的第七阶模态作为第一阶模态来处理。详细分析了制动盘跟摩擦片的前六阶模态。

4. 盘式制动器主要部件的模态分析

4.1. 制动盘的模态分析

制动盘的1~6阶模态振型如图3所示。制动盘的1~6阶固有频率如表2所示。通过对制动盘的模态分析得出：第一阶的频率和振型是966.94 Hz和弯曲变形，制动盘的最边缘处有四处较大的应变。第二阶的频率和振型是966.98 Hz和弯曲变形。第三阶的频率和振型是1880.88 Hz和伞状，应变均匀分布在制动盘的周边。第四阶的频率和振型是2481.37 Hz和弯曲变形，6处最大的变形在制动盘的周边。第五阶的频率和振型是2481.44 Hz和弯曲变形。第六阶的频率和振型是2920.16 Hz和弯曲变形。通过以上的分析可以看出，制动盘的最大应变基本都在制动盘的边缘处，同时也是最易引起刹车噪音的部分。

4.2. 摩擦片的模态分析

摩擦片的1~6阶模态振型如图4所示。摩擦片的1~6阶固有频率如表3所示。通过对摩擦片的模态分析得出：第一阶的频率和振型是843.60 Hz和弯曲变形，最大的变形出现在摩擦片的两端。第二阶的频率和振型是1337.02 Hz和弯曲变形，摩擦片的四周有着4处较大的变形。第三阶的频率和振型是2088.94 Hz和弯曲变形最大应变值仍然出现在摩擦片的两端。第四阶的频率和振型是2407.85 Hz和弯曲变形。第五阶和第六阶的频率分别是2818.02 Hz和3758.80 Hz。

4.3. 制动盘与摩擦片固有频率对比

从表2和表3可以得知，随着模态阶次的增加，由于模态阶次的增加，制动盘和磨擦片的固有频率都呈增加现象。同时，制动盘和磨擦片的一阶固有频率分别为966.94 Hz和843.60 Hz，四阶固有频率分别为2481.37 Hz和2407.85 Hz，所以制动盘和磨擦片的一阶固有频率与四阶固有频率相对接近，易于形成共振。由此可见加大了对盘式制动器有限元计算的深入研究，对于进行协同优化设计也是十分必要的。同时考虑到制动片材料的特点，可通过改善其厚薄或是在尖角处倒角的方法改善其固定频率，进而减少了制动盘与磨擦片间共振的产生，进而降低了刹车噪音以及提高行车安全性。

图3. 制动盘的1~6阶模态振型图

表2. 制动盘1~6阶固有频率

5. 结论

论文中以盘式制动系统为重点的研究对象，首先使用UG对盘式制动主体的零部件制动盘和磨擦片完成了建模，并利用HyperMesh软件对制动盘和磨擦片完成了有限元模态分析，得到如下结论：

1) 通过使用HyperMesh软件对盘式制动器的主要零部件进行了模态分析，获得了1~6阶模态振型图。从这些图中可以得知制动盘的应变主要集中在边缘处，产生这种情况的主要原因是制动盘固定位置为中心定位孔处，存在约束使得振动过程中变化较小甚至基本无变化，摩擦片的应变发生在两端。

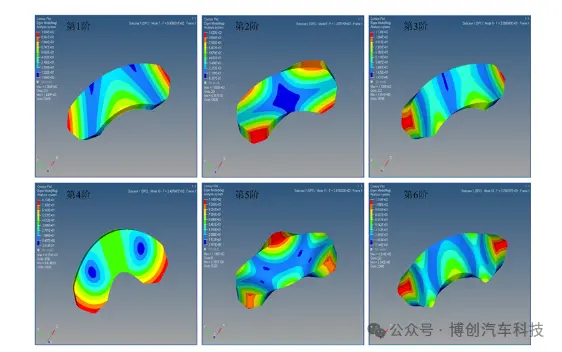图4. 制动盘的1~6阶模态振型图

表3. 1~6阶固有频率

2) 对制动器重要部分的固有频率做出了比较。由于模态阶次的提高，制动器重要部分的固有频率均出现了增长态势。其制动盘与摩擦片之间的一阶固有频率与四阶固有频率都相当接近，易于形成共振。为今后的商务车制动器设计于优化提供了一定的理论依据。

参考文献

[1]王正国, 钟宏民, 付磊, 孙泽刚. 不同摩擦衬片结构下盘式制动器瞬态热机耦合特性研究[J]. 机械设计, 2020, 37(3): 77-85.[2]赵军, 许建民, 葛晓宏, 李辉. 汽车制动盘的有限元模态分析[J]. 装备制造技术, 2014(12): 58-60.[3]高若奇, 付道琪, 杨志峰. 考虑温度系数的盘式制动器热力耦合分析[J]. 农业装备与车辆工程, 2021, 59(2): 110-112+117.[4]曾昱皓, 谢松成, 杨荣松. 基于ANSYS Workbench的新型盘式制动器的强度分析和模态分析[J]. 机械, 2020, 47(1): 23-29.[5]董慧丽, 鲍久圣, 阴妍, 郭超勋, 黄山, 赵少迪. 盘式制动器摩擦噪声特性的试验分析[J]. 摩擦学学报, 2020, 40(2): 175-184.[6]周昌祁, 余晓星. 盘式制动器制动噪声影响因素的有限元分析[J]. 汽车工程师, 2011(1): 44-47.[7]施佳辉, 王东方, 缪小冬. 简谐载荷下的盘式制动器振动噪声分析及试验[J]. 西华大学学报, 2019, 38(5): 36-42.[8]张立军, 陈远, 刁坤, 孟德建. 盘式制动器接触压力与热机耦合特性仿真分析[J]. 同济大学学报, 2013, 41(10): 1554-1561+1578.[9]李志刚, 何春, 郑彬. 汽车盘式制动器有限元分析与结构优化[J]. 机械设计, 2021, 38(S1): 79-82.