广告
分布式驱动车辆轨迹跟踪与稳定性多智能体协同控制研究
2025-03-19 08:55:44· 来源：智能运载装备研究所 作者：杜志彬
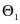根据是否存在具有强制性约束来达到最优联合决策的协议，将博弈划分为两类：协同博弈及非协同博弈。对于分布式驱动车辆而言，前轮转角受控于线控转向系统，而附加横摆力矩则是通过合理的对四个驱动电机扭矩进行分配得到。两套执行器都是独立运行，因此它们可以被视为两个独立的博弈者，将其分别命名为博弈者
及博弈者
。对于博弈者
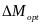，在其单独的任务中将通过施加最优前轮转角来取得最优的路径跟踪表现。同样，对于博弈者
，将通过施加最优附加横摆力矩来尽可能的保证车辆的横向稳定性是其单独的任务。博弈双方都基于可知的信息来寻求最优控制输入来最小化自身的损失，因此，在选择自身的控制输入时，它们可以被视为自私利己的个体。综上，将上述关系建模为两智能体非协同博弈，具体表达如下：
及博弈者。对于博弈者，在其单独的任务中将通过施加最优前轮转角来取得最优的路径跟踪表现。同样，对于博弈者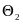，将通过施加最优附加横摆力矩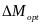来尽可能的保证车辆的横向稳定性是其单独的任务。博弈双方都基于可知的信息来寻求最优控制输入来最小化自身的损失，因此，在选择自身的控制输入时，它们可以被视为自私利己的个体。综上，将上述关系建模为两智能体非协同博弈，具体表达如下：
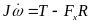(35)
其中，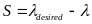
表示博弈者的数量，在本文中
；
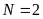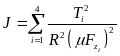为博弈者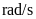
的所有可行策略集合；
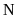为博弈者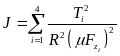的损失函数，在本文中将其设计为二次函数形式，具体如下所示：
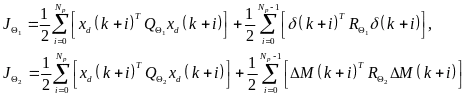(36)
其中，为预测域。式(36)中的权重矩阵定义如下：
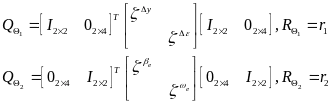(37)
其中，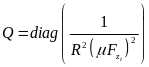
，
，
、、
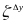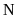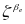、分别代表四个状态变量的权重系数；
、
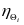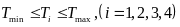分别为前轮转角控制输入、附加横摆力矩控制输入的权重系数。
（4）控制器设计
在动态博弈中，信息模式是一个十分重要的属性，不同的信息模式将会得到不同的最优策略。如果每个博弈者只知晓博弈的初始状态则将该博弈称为开环信息模式。相反，如果每个博弈者能够获悉在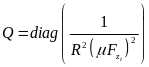步内其他博弈者的策略，则称该博弈为闭环信息模式。在本部分，将基于开环博弈策略完成控制器的设计。
在推导最优策略之前，平衡点的类型是动态博弈中另外一个核心点，将首先对其进行阐述。假设博弈双方同时做出各自的决策，即不存在领导者及追随者，在这种情况下，纳什平衡将被应用。在纳什平衡中，没有任何一个博弈者能够通过改变其自身的策略而获得比原策略更大的收益。因此，当处于纳什平衡时，将满足下述不等式：
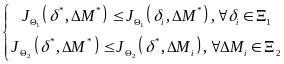(38)
其中，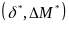
为纳什平衡点，即上层控制器所要解算得到的控制输入量。
对于优化问题式（38），哈密顿函数如下所示：
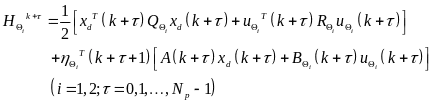(39)
其中，下标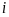
用于区分不同的博弈者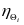，为伴随变量，其满足下述伴随方程及终端约束：
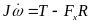(40)
此外，开环博弈的纳什平衡点必须满足下述方程：
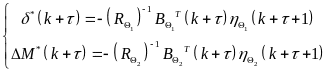(41)
广告 
最新资讯
-
整车性能测试体系：汽车试验工程的基本框架
2026-03-10 12:54
-
联合国法规R76对轻便摩托车前照灯远近光性
2026-03-10 12:15
-
联合国法规R75对摩托车与轻便摩托车气压轮
2026-03-10 12:14
-
联合国法规R74对L1类车辆灯光与光信号装置
2026-03-10 12:14
-
联合国法规R73对货车侧面防护装置的工程化
2026-03-09 12:14
