广告
汽车数值风洞的前世今生（上）
2018-02-26 11:50:25·
CFD是计算流体力学（Computational Fluid Dynamics）的简称，是通过计算机数值计算和图像显示，对包含有流体流动和热传导等相关物理现象的系统所做的分析。通过CFD数值模拟，能使我们更加深刻的理解问题产生的机理，为实验提供指导，节省实验所需的人力、物力和时间。接下来的三期作者将和你一起聊聊数值风洞的前世今生，具
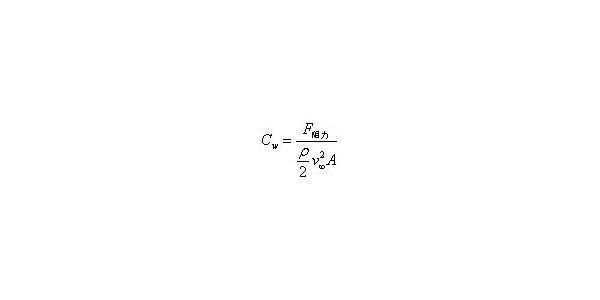
CFD是计算流体力学（Computational Fluid Dynamics）的简称，是通过计算机数值计算和图像显示，对包含有流体流动和热传导等相关物理现象的系统所做的分析。通过CFD数值模拟，能使我们更加深刻的理解问题产生的机理，为实验提供指导，节省实验所需的人力、物力和时间。接下来的三期作者将和你一起聊聊数值风洞的前世今生，具体内容参见本期引言。
引言
“非常想聊聊CFD，但是却不想掉进复杂的偏微分方程的漩涡之中，因为在那里面蜗牛君自己也会被淹死 ！”这是本文最重要的前提。
本期蜗牛君将会就自己视野范围之内，说说流体力学、计算流体力学以及其应用于汽车气动力计算的历史，蜗牛君会尽量不使用数学语言。
在后两期中，将会分享蜗牛君在工程应用中总结的一些CFD技术细节。
敬请期待！
蜗牛君不负责任的声明
CFD技术是长期以来流体力学、数学和计算机科学发展的重要成果。如果希望对它进行详细、严谨说明的话，必须使用数学语言进行描述。
虽然，蜗牛君曾经多次尝试着“啃”那些错综复杂的偏微分方程，但是——
幸好，作为工程应用人员，蜗牛君可以在很大程度上“投机取巧”。
因此在本文中，我将尽量避免使用各种公式。但是由此必然会带来一些含混不清和歧义，敬请谅解！
经过几十年的发展，CFD技术的应用已经渗透到汽车开发过程中的很多领域。包含气动力、热传导和气动声学现象的所有整车、零部件的开发工作，几乎都有应用。
由于篇幅所限，这篇文章将仅针对气动力的CFD计算展开。
标题中的“数值风洞”一词，主要是指用CFD方法预测整车气动力的计算。
.流体力学发展简史
不说废话，直接上干货！
1678年：牛顿对阻力的研究获得初步成功，并提出粘性流体的剪应力公式。
1732年：H. 皮托发明了测量总压的皮托管。
1738年：伯努利提出著名的定常不可压缩流体的伯努利定律。
1748年：M. W. 罗蒙诺索夫提出质量守恒定律。
1752年：L. J. R. 达朗伯依据质量守恒定律，提出流体的连续性方程。
1775年：L. 欧拉提出无粘性流体的运动方程组。
1781年：J. L. 拉格朗日提出拉格朗日定理，并且进一步的完善了无粘性流动的基本理论。
1808年S. D. 泊松和1848年G. G. 斯托克斯：建立了间断面前后流动参量所满足的关系式。这是对可压缩气体运动的理论研究的开始。
1822年：J. R. 傅里叶提出了傅里叶导热公式。
1823年L. 纳维和1845年G. G. 斯托克斯：分别用不同的假设和方法，提出了不可压缩和可压缩流体的运动方程组（NS方程），从此，开始了粘性流体运动的研究。
1852年：F. 雷什提出了重力作用下流体流动的相似性参数--雷什数（佛罗德数）。
1855年：A. 菲克提出了菲克定理。
1856年：H. P. G. 达西提出了达西公式。
1883年：O. 雷诺对不同直径的圆管进行了一系列的实验，发现流动有两种状态--层流和湍流。并提出无量纲参数--雷诺数。
1895年：O. 雷诺引进了雷诺应力的概念，并用时均的方法，建立了不可压缩流体做湍流运动时满足的方程组。雷诺的研究为湍流的理论奠定了基础。
1904年：L. 普朗特在自建的水槽中进行了大量的测量和仔细观察之后，提出了著名的边界层理论。
1912年：T. von 卡门从理论上分析了涡的稳定性。
1921年：T. von 卡门提出了求解边界层的动量积分关系式。
1947年：第一台电子计算机问世，数值方法得到了迅速的发展。
1950年J. von 诺伊曼与1963年W. F. 诺：分别提出显式，隐式的人工粘性的概念。
1950年后，流体力学的研究内容有了明显的转变。研究学者们转而研究石油、化工、能源、环保等领域的流体力学问题。并与其它学科进行交叉形成新的学科如计算流体力学、可压缩气体力学、多相流体力学、稀薄气体力学等。
1968年：首个以CFD为主题的大会在美国Monterey召开。
1969年：Spalding创立了第一个CFD咨询公司--CHAM。
1972年：Patankar和Spalding提出了著名的SIMPLE算法。
1984年：Fluent软件诞生，直至后来被ANSYS公司收购。
本章小结分界线
这节终于写完了。
上面的内容，是蜗牛君从微信公众号“CFD届”中搬运并整理而来的，那是一个非常好的号，有很多高质量的文章，推荐小伙伴们关注。
上面表述中的关键问题，蜗牛君附图进行了“调戏”，它们分别对应几个最重要的概念：
（1）牛顿流体的粘性剪应力定理；
（2）理想的无粘流体欧拉公式；
（3）一直让蜗牛君仰视的NS方程；
（4）神秘的“湍流”；
（5）让人纠结的“边界层”。
蜗牛君觉得，清晰的理解这些概念，是进行CFD工程应用的重要基础。
汽车周围流场的特点
从上文中可以看出，流体力学的理论发展可以追溯到300多年前，而CFD的真正发展不可能超过70年，工程应用更是只在上世纪60年代之后才开始。
大家都知道，空气动力学在航空领域的重要性远比汽车行业高，不难想象CFD的应用也是这样。但是汽车行业的前辈们，也在CFD开始工程应用后的第一时间进行了很多探索工作。
在介绍CFD方法在汽车上的应用之前，首先需要明确汽车流场的特点，将这些特征牢记于心，可以更好的理解目前CFD代码的仿真能力，并且对结果进行更加客观的解释。
围绕路面车辆周围的流场的典型特征是：三维；流动方向和垂直方向上都存在陡峭的压力梯度以及封闭的或者开放的分离流动区域。
在车身附件上，会发生较小的封闭分离流动区域，例如头灯、后视镜、门把手、风窗雨刮、发罩风挡玻璃连接处等。更大的三维分离区域发生在A柱、车身后端、车身下侧和轮胎腔中。
路面车辆运行环境的特征是：几乎一直会存在环境风。车辆的速度和运动方向，与自然风不同。结果产生的偏航气流是不对称的，并且在下游保持分离，它叠加到复杂的外流场中。在分离流动本身固有的非稳态属性中，周围环境随时间的变化，给流场增加了双重的时间历程特征。旋转的车轮和离地间隙，是强烈影响车辆下部和侧面气流的典型特征。
上面这段文字是蜗牛君从大神WHCHO W.H的书中搬运过来的。其中的两个关键词是：“分离”和“非稳态”。
由于我们实际上关注的是气动力的时间平均值，因此最重要的关键词是
汽车数值风洞的应用历史
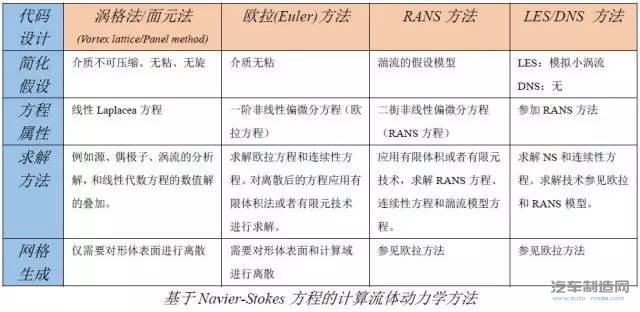
上表给出了主要的CFD计算方法：从左至右，各种方法所考虑的物理现象逐渐增加；方程的复杂程度也逐渐增加；所需要的计算资源不断上升；应用于工程实践的时间点也是不断后移的。
由于分离流动和粘性直接相关，所以忽略粘性的方法，在汽车上的应用价值就大打折扣了。另外，由于受所需要的计算资源的限制，现在在汽车领域真正的应用DNS方法，实际上是不可能的。
因此，从汽车行业工程应用的角度，蜗牛君将上面的四种方法分成三代。
第一代为忽略了粘性的面元法和欧拉方法；第二代是目前正在应用的RANS方法、LES方法；第三代是未来可能应用的DNS方法。
前辈们的工作
从20实际70年代开始，前辈们开始探索将“面元法”应用于汽车的表面压力计算，并且不断的优化这种方法，使它尽量的适用于汽车领域，这些探索一直持续到90年代初。
面元法只需要数千个面网格就可以进行计算了，但是它的主要缺点是，无法“自动”的仿真分离现象，如在车辆表面的分离、在A、C柱上形成的纵向涡流（longitudinal vortices）等。这些现象需要基于经验进行人为的模拟。
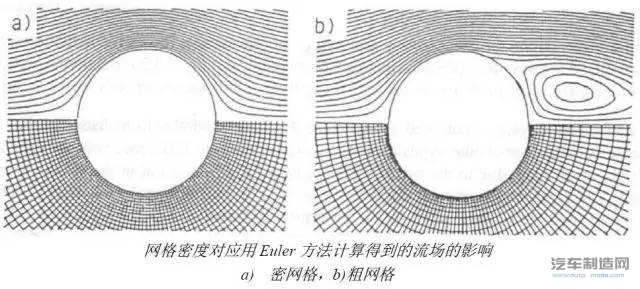
欧拉（Euler） 方法的最大缺陷也是模型中没有粘性，因此不能真实的仿真出分离现象。这种方法在实际应用中所表现出的分离现象，实际上是一种受数值计算过程影响的“假分离”，这种分离现象是直接受网格影响的。
在20世纪80年代前后，Euler 方法（耦合边界层计算）曾经被用于研究汽车的外部流动和内部流动。后来随着计算机技术和RANS方程求解技术的显著进步，汽车空气动力学者逐渐对Euler方法失去了兴趣。
CFD终于具有真正的工程价值了！
几乎所有目前工程上应用的所谓稳态CFD方法，都是基于时均形式的NS方程来求解的。
在这些方程中，粘性力被包含在这些流动的力平衡方程中。
对于路面车辆而言，人们感兴趣的外部流动是湍流。就像之前提到的，湍流中的速度和压力，不仅仅是空间坐标x、y、z的函数，而且是时间t的函数。
基于Q.REYNOLDS的早期工作，非稳态湍流被分为稳态（与时间无关的）平均运动和非稳态（时间相关的）运动两部分。
平均值是在一定的时间间隔内评估的，间隔足够长，速度和压力的平均值就变得与时间无关；而且很明显波动量的时间平均值为0。
将平均值和波动值的概念引入到非稳态NS方程中，就获得了稳态形式的NS方程，被称为雷诺平均NS方程（Reynolds Averaged Navier Stokes -RANS）。
平均处理的结果是，NS方程组中包含了比方程数更多的未知数。必须首先找到某种方式建立附加的方程来联系平均流动中的这些未知变量。也就是应用被称为“湍流模型”的方程，来“封闭”RANS方程。
值得一提的是，通过这种方法进行计算，仅仅是模拟了湍流运动中的平均流动的作用，并不会计算速度和压力的波动分量。
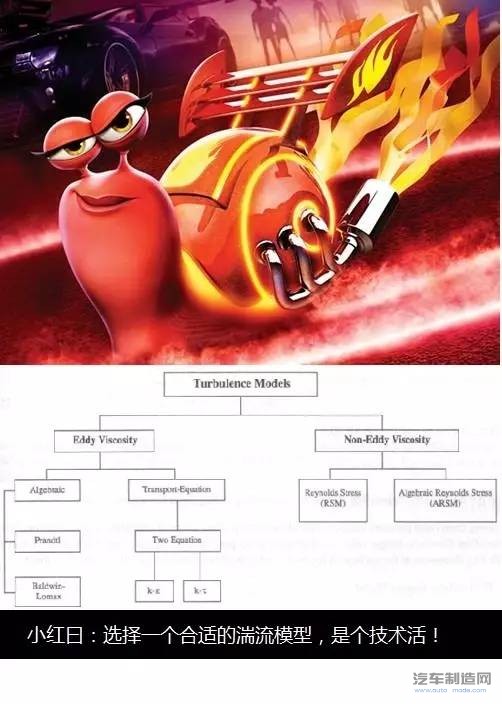
从上面的描述中，大家可以发现，对于RANS方法来说“湍流”模型是个非常重要的存在。
在20世纪80年代末和90年代，发表了很多应用RANS代码进行车辆内部和外部流场仿真的文章。其中的一些代码同网格生成前处理器、数据后处理分析软件一起，已经被作为全面的软件包商业化了。
当时所应用的计算网格规模在几十万到100万之间。其中包括很多实验结果同计算结果之间的对比工作。
目前工程应用的瞬态方法中，大窝模拟方法（Large Eddy Simulation--LES）是比较重要的一个。
它的基本假设是，在湍流中，不同尺寸的涡流结构同时出现。其中，由大的涡流结构从平均流动中吸收能量。它们倾向于更强烈的各向异性、是更“自然”的涡流、并且更依赖于边界条件，而且它们输运主要的湍流动量和能量。
通过非线性的相互作用，它们将自身的一部分能量传递给更小尺寸的涡流结构。小结构涡流的主要作用是，耗散大结构涡流提供的能量，并且它们倾向于各项同性。小涡流们几乎具有“统一的”特性（即同边界条件无关），并且输运相对小的能量和动量。
在计算程序中，大尺寸的涡流被真实的计算出来；于此同时，亚格子尺寸的涡流（subgrid-scale eddies）的效果是模拟出来的。
在蜗牛君了解的范围之内，目前计算机硬件的发展，已经可以支撑LES方法和DES方法（分离涡方法，近年逐渐得到发展，它实际上是RANS方法和LES方法的混合）这样的瞬态计算方法的工程应用了。
CFD的未来
求解瞬态的NS方程，所有必需尺寸的湍流运动都被计算出来，并且不使用近似模型，这就是直接数值模拟（DNS）。它对计算机和数值方法都提出了巨大的挑战。DNS方法所需的网格节点数，随雷诺数的9/4次方增长。
因此，以目前可以获得的计算资源来说，DNS方法对于工程应用是不适用的。它仅仅被局限在低雷诺数（大约5000）并且非常简单的流动形式上。
在20世纪90年代，日本的汽车工程师进行了一些DNS方法应用于汽车领域的尝试。当时日本CFD仿真的一般特征是：应用非稳态不可压缩NS方程；不使用任何的湍流模型；网格节点数量在1百万的量级；基于车身长度的雷诺数大约为1百万。
目前看来，这种方式实际上是一种“无意识的”并且“不受控制的”LES方法，它包含求解大尺度的涡流结构、并且小尺度的模型由数值粘度（或误差）来模拟。
尽管如此，它还是产生了大量的有价值的设计信息。这些工作可能是在通往DNS道路上的一种练习。在将来可以获得充足的、经济的计算资源，从而可以实行DNS计算时，它们在前处理、后处理以及数值方法上都可以提供有效的经验。
那么真正原汁原味的DNS是怎么样的呢？F.Xavier Trias在2014年用DNS方法，计算了一个雷诺数为22000的方柱扰流，共使用了3亿网格，计算结果是这个样子的
本期小结
一不小心写了这么长，结尾就不多啰嗦了。
蜗牛君觉得，回顾历史对当前的应用和未来探索不但是有帮助的，而且是必要的。
希望这些东西对大家能有帮助！
我们下期再见！
作者简介
李涛 先生
中国汽车工程学会汽车空气动力学分会委员，北京新能源汽车股份有限公司整车性能部整车CFD分析及风洞实验主管工程师，负责项目开发过程中的整车CFD分析工作。
李涛先生自营公众号“路面车辆空气动力学”，自谦为“缓慢但坚韧的蜗牛君——汽车空气动力学专业知识的搬运工！” - 下一篇：汽车数值风洞的前世今生（中）
- 上一篇：中国汽研汽车风洞建设启动暨风洞联盟签约仪式
广告
广告
最新资讯
-
NVIDIA 发布 2025 财年第三季度财务报告
2024-11-21 13:30
-
Mack卡车为买家推出创新的虚拟现场探索体验
2024-11-21 13:29
-
氢燃料电池卡车从1到100要多长时间？戴姆勒
2024-11-21 13:28
-
聚焦消费者用车极限环境，2024中国汽研汽车
2024-11-21 13:21
-
新能源汽车高寒环境可靠性行驶试验研究
2024-11-21 13:19
广告
广告
