寻找供应商
广告
首页 > 空气动力学 > 正文

汽车数值风洞的前世今生（中）

2018-02-26 11:52:35·  
　
引言从某种程度上来说，所谓数值风洞就是用数值计算来复现这些物理现象。为了清楚的说明汽车风阻的成因，必须要详细的说明粘性的作用、边界层的发展等理论问题。但是，蜗牛君只是一个不太严肃的工程人员，并且害怕长篇大论会使得一些小伙伴放弃继续阅读。所以，希望仍然坚持不使用数学语言的原则，但是由此必定会引起一些错
引言
 
从某种程度上来说，所谓数值风洞就是用数值计算来复现这些物理现象。
 
为了清楚的说明汽车风阻的成因，必须要详细的说明“粘性”的作用、边界层的发展等理论问题。
但是，蜗牛君只是一个不太严肃的工程人员，并且害怕长篇大论会使得一些小伙伴放弃继续阅读。
所以，希望仍然坚持不使用数学语言的原则，但是由此必定会引起一些错误。
 
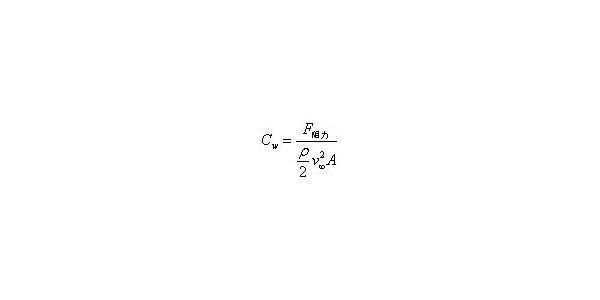
经常被滥用的公式
首先，必须要说一个经常被滥用的公式——“伯努利方程”。
伟大伯努利方程（Bernoulli’s equation），将沿着流线的压力和速度联系在一起。在非粘流场中，沿着某一流线，静压和动压的和为常数。它指出，在局部速度高的位置会出现低压力，反之亦然。
在非粘性流场中，将所有车身表面的X向压力进行积分，结果产生的阻力将为0。
此结果就是著名的达兰贝尔悖论（Alembert's paradox），它表明在不可压、非粘性二维流场中，不会产生阻力。
由于这种没有切向力的流场产生的结果，明显的与真实情况不同，它已经被前辈们定义成为是不可信的理论了。
但是处理车辆周围的非粘性流场，仍然是非常有意义的。通过对比车辆周围的真实流场（既粘性流体流场）和理想流场（既无粘性介质的流场）之间的区别，可以对产生风阻的物理机理，进行很好的解释。
 
粘性都对流场做了什么？
还记得上一期，我们提到的真实汽车外流场的关键词吗？
 
没错，在没有粘性的世界里，气流会永远附着在固体表面运动。正是“粘性”的出现，导致了气流分离现象。
气流分离到底是怎么产生的？
粘性这个讨厌的东西，不但会拖慢蜗牛君的脚步，也使得流动方程变成二阶偏微分方程。
幸好前辈们发明了“边界层”这么个概念，也就是仅在固体壁面表面一个很薄范围内，才考虑粘性，在其它的绝大部分空间，认为流场是没有粘性的。
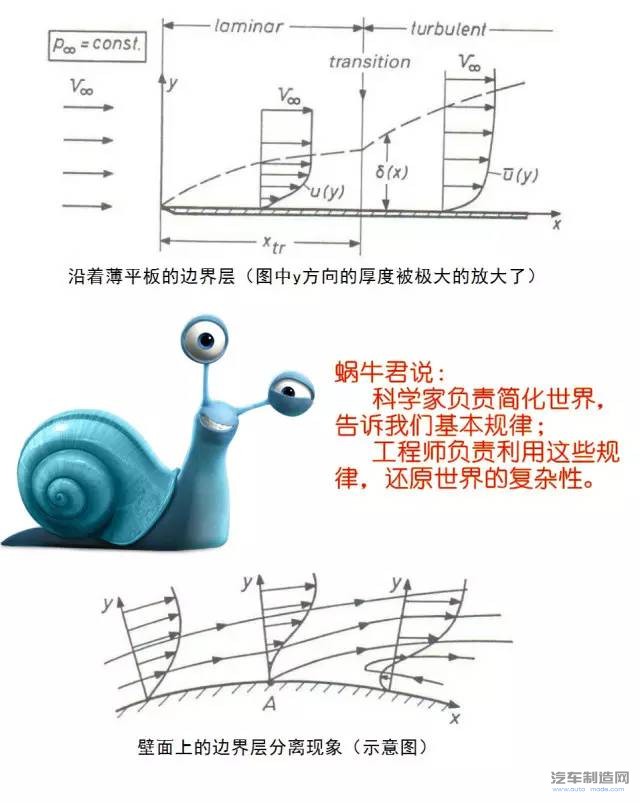
在平板边界层的初始阶段，边界层流动稳定的平行于壁面。这叫层流边界层，它的厚度依赖于距离和粘度的增加而增加。在某一个位置，会出现所谓的层流边界层向湍流边界层的转捩。转捩的位置会受到雷诺数、表面的粗糙度和流动方向上的压力梯度的影响。在一般情况下，对于中等的雷诺数而言，层流到湍流的转捩发生在压力最小的位置，并且随着雷诺数的增加，转捩点向上游移动。
 
在湍流边界层的区域，流动基本上为瞬态的。虽然时间平均的流动仍然是附着的，并且（几乎是）平行于壁面的。但是流动中的波动部分实际上已经不再附着在壁面上了。
 
如果在流动方向上压力增加的话，会阻碍边界层流动（特别在近壁面位置）甚至最终导致反向流动。在方向向前和向后的流动之间，具有一条气流离开壁面的分离线，此种现象就被称为分离（separation）。
 
需要强调的是，相对于层流边界层而言，湍流边界层能够承受更加陡峭的逆向压力梯度而不产生分离现象。这是由于湍流扰动过程，可以使得壁面附近的边界层，从外部流场“借来”更多动量，用以克服逆压梯度。
 
上面描述的是一个完整的气流分离过程，蜗牛君将这种磨磨唧唧、犹犹豫豫的分离想象，称为“谢霆锋-张柏芝”式的分离。只有在比较圆滑的表面上，才有机会看到它。
其实在汽车上更常见的，是一种简单粗暴、没有任何预期的“王宝强-马蓉”式的气流分离。
这种现象，发生在形体表面的曲率“突然”变化的位置；用“人类的语言”来说，就是在那些有棱角的位置上。
也就是说，在汽车车身上，由于车身突出物和附件的影响，大部分分离现象发生的位置几乎是固定的，而并不是边界层发展的产物。例如发罩前端、发罩-风挡玻璃连接处、A柱位置、顶盖后端和车外后视镜等。
在这个小世界中空气 “真实”的掠过汽车表面；在粘性的作用下，“创造”出边界层，并让它逐渐发展、变厚；无序的湍流很讨厌，但是严谨的“算命先生”也考虑它的影响；边界层的发展，最终导致了气流分离，形成一个个或大或小的分离区。
 
作者简介
李涛 先生
中国汽车工程学会汽车空气动力学分会委员会委员，北京新能源汽车股份有限公司整车性能部整车CFD分析及风洞实验主管工程师。负责项目开发过程中的整车CFD分析工作。
 
李涛先生自营公众号“路面车辆空气动力学”，自谦为“缓慢但坚韧的蜗牛君——汽车空气动力学专业知识的搬运工！”  
分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• 采用分析方法对 FSAE 方程式赛车进行空气动力学研究 • 运动摩托车的阻力优化
• CAERI风洞丨车门动态变形量测试能力 • 横风下超车时汽车瞬态气动力和动态响应的耦合分析
• 广汽风洞实验室：国内车企首个全尺寸气动—声学风洞实验室 • 动力电池液冷冷板通道拓扑优化设计
• 国内首台套二维全自动汽车正投影面积测量系统研制成功 • CAERI数值风洞软件发布成功，开启新一代CFD仿真分析解决方
• CAERI数值风洞软件、PartoX复杂流场仿真软件发布 • 中汽中心风洞中心|实验能力介绍（一）
0 条相关评论
  • 广告
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026917号-25