模态空间—结构动力学修改(SDM)该如何使用
嗯……我们来讨论一下。

作者:Peter Avitabile 翻译:倪昊、焦吉祥(德国m+p国际公司)
在19世纪80年代初期,结构动力学修改(SDM)就已经成为一种被广为使用的工具。由于对这项技术理解的偏差,可能会得到某些错误的结果。但如果使用在正确的条件下,SDM是一种非常强大的工具,可以帮助设计工程师做出很好的设计决策。我们首先简要回顾一下这项技术,并且说明一下这项技术最大的问题——模态截断,是怎样影响其结果的。
基本上来说,SDM是一种分析工具,用于预测当被研究对象的质量、阻尼、刚度产生变化时,其动力学特性的改变。这里要注意,预测仅仅需要模态数据(频率、阻尼、和模态振型)——而不需要对原始的FEM或试验数据进行修改。然而,如果一旦得到了一些想要的变化,那么强烈建议重新对修改后的模型进行有限元分析或者重新对修改后的试件进行试验。
对于研究对象,可列出其物理系统方程并得到特征解。模态表达式既可以从解析模型中得到,也可以从试验数据中得到。在模态空间中,物理系统的模态表达式按下式给出:
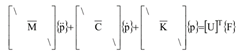
现在,物理系统的质量变化量∆M、阻尼变化量∆C、和刚度变化量∆K,可以在模态空间中表示(通过模态变换方程)如下
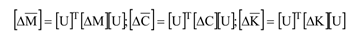
假设结构为比例阻尼系统,可以得到修改后的系统的特征解。这个解的一个重要部分是由下式求解得到系统的最终物理模态:
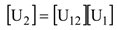
该式表明被修改过的系统的最终修改后的模态是由原始系统无修改模态的线性组合构成。这是一个重要的方程,我们将它用来说明模态截断对预测结果的影响。
现在看一个简单的自由-自由梁的例子,我们将对它进行两种简单的结构修改——简支梁和悬臂梁。将利用两根接地弹簧来修改结构,并求解SDM方程以得到修改频率和模态振型。原始无修改频率和最终修改频率如表1所示(备注:识别出的用斜体表示的频率是系统约束模态的一种近似,超出了本次讨论的范围)。
注意,仅仅利用原始无修改系统的前五阶模态,简支梁生成了非常精确的修改模态,而悬臂梁却没有。为什么简支梁表现得如此良好,而悬臂却不行呢?答案在于这些模态振型是怎样由原始系统模态来构成的。
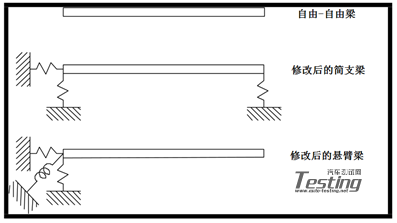
图1
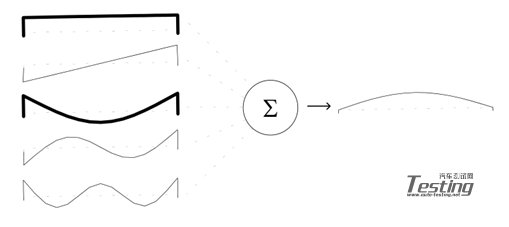
图 2
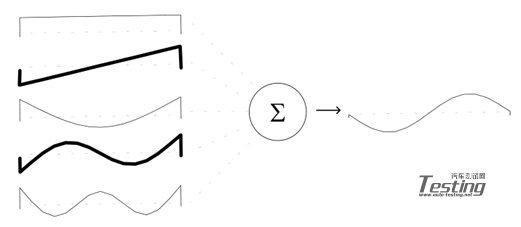
图 3
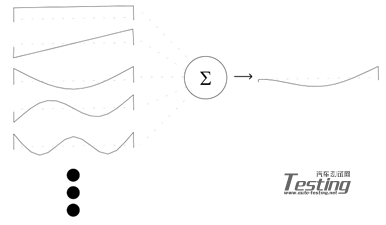
图 4
这个简支修改后的模态很容易由原始系统无修改模态的线性组合构成。当观察图2时,我们注意到第一阶模态和第三阶模态是简支梁的第一阶最终修改后的模态的最重要贡献者。而当观察图3时,我们注意到,第二阶和第四阶模态是简支梁的第二阶最终修改后的模态的最重要贡献者。
但是当我考虑悬臂梁修改的模态时,无修改系统的所有五阶模态都有重要的贡献。事实上,需要更多的模态来提高这个悬臂梁预测模态的精度。(备注:悬臂梁的第二阶模态如图4所示)
可以证明,简支梁可以简单地由原始系统已有的5阶自由-自由模态的线性组合构成,而悬臂梁却不能!事实上没有所有阶模态参数并不是问题。真正的问题在于,最终修改后的模态必须能够由原始无修改模态线性组合构成。
另一个值得注意的要点是,自由-自由梁的刚体模态对于准确预测修改后的模态非常重要。如果没有刚体模态数据,那么这个预测模态将是错误的。对于开发试验模态数据库来说,这是一个重要的注意事项,因为通常不会将刚体模态作为试验的组成部分来进行采集。
从本质上来说,为了利用SDM求得准确的修改模型,最终模态必须总是由无修改模态的线性组合构成。如果这是可能的,那么可以得到准确的结果。如果这是不可能的,那么由于模态截断将会产生较大误差。
此处略去数学方程,用几个简单的图形来说明SDM是如何利用系统无修改模态来获取系统修改后的模态的估计值。我希望这个讨论可以帮助你理解SDM可能受到模态截断的影响。如果您有关于模态分析的任何其它问题,欢迎垂询。
最新资讯
-
大卓智能端到端直播实测,16公里复杂路段挑
2025-04-25 17:16
-
《汽车轮胎耐撞击性能试验方法-车辆法》等
2025-04-25 11:45
-
“真实”而精确的能量流测试:电动汽车能效
2025-04-25 11:44
-
GRAS助力中国高校科研升级
2025-04-25 10:25
-
梅赛德斯-AMG使用VI-CarRealTime开发其控制
2025-04-25 10:21





 广告
广告





























































