模态空间—质量载荷与数据一致性对模态参数估计的影响
让我来解释一下。

作者:Peter Avitabile 翻译:倪昊、焦吉祥(德国m+p国际公司)
这是另一个在模态参数识别中让人感到困惑的范例。当曲线拟合结果令人迷惑或者看上去不正常的时候,人们总会把这些现象归咎于噪声或非线性。这常常是一句空洞的话,当不理解或者不能轻易解释某些现象的时候,很多人会使用这句话。让我们看一看为什么数据一致性很重要,质量载荷会有什么影响。
首先要回忆的事情是,我们用以拟合数据的模型是根据一个线性、对称的方程组,其极点(频率和阻尼)被定义为全局物理量,并且认为其互易性成立。现在只要我们的数据与该模型吻合,则万事具备。但如果数据有偏差会该如何呢?
我们来考虑一个简单平板的试验,采用一套8通道的数据采集系统,通过两个激振器激励进行MIMO试验。现在,如图1所示,对安装于平板之上的6个加速度计,我将利用高精度的测试技术来采集FRFs,以保证得到尽可能最优的测量结果(第1次试验时测量实心点,第2次试验时测量其它点,并且通过在结构上移动加速度计来得到这些测点的数据)。
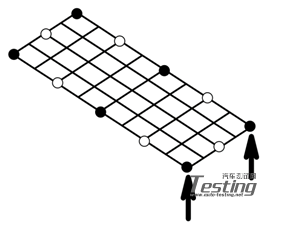
图1-MOMO方式分两批次试验
图2显示的是模态指示函数(MIF),图3是稳态图。仅仅提取前2阶模态的极点(作为示例)。稳态图非常清楚地指出了这两个极点。注意,随着模型阶数的增加,很清晰地确定了极点(跟求和函数重叠在一起)。一旦提取出极点,就可以得到留数或振型,这样就得到了与这6个测点相关的模态数据。图4显示了一个典型的曲线拟合。
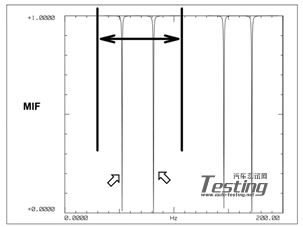
图2 第一批次试验MIF函数
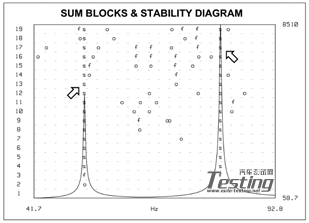
图3 第一批次试验稳定图

图4 第一批次试验曲线拟合结果
可是,第1组数据仅仅包含6个测点。为了更好地确定模态振型,需要更多的测点。
对于其余的测点,将加速度计移动到图示的测点上(空心点),这样采集到了第2组MIMO测量结果。这一次也是仅仅利用第2组测点来提取极点,并得到稳态图。这一次也清晰地确定了极点,以及与这6个测点相关的模态振型。(此处,没有显示这些测量结果,但其与第1次情况类似。)但是这两组数据是分别求值来估计极点和留数的。
现在,我们将这两组数据合在一起求值。重新计算模态指示函数和稳态图。现在在相同的频带内,我们在模态指示函数上看到的不是之前观察到的2个明显的峰,反而是4个明显的峰(图5)。之前用过的相同频带(图6)现在指示出了4阶模态,而不是2阶模态!这怎么可能?平板没有变化不是吗?
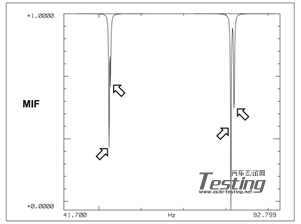
图5 第一&二批次试验整合后的MIF函数
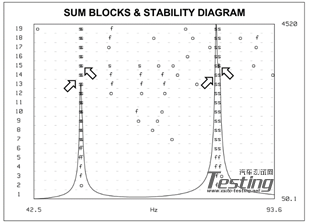
图6 第一&第二批次试验整合后稳定图
嗯,平板是没有变,但试验布置却改变了!移动的加速度计具有质量影响,引起了模态频率的些许偏移。所以当同时处理所有数据时,有些测量结果指示出极点在某一个频率上,而其他测量结果却指示出极点在另外一个频率上。
那么哪一个是对的?似乎两个都不对。这是因为试验设置对系统的模态产生了影响。问题是哪些极点是正确的,可以用于模态参数估计。嗯,对于所有的测量结果,你确实不能确定一组全局的极点,因为它们对于所有测量结果而言并不是“全局的”。实际上,在这种情况下,正确提取参数的办法是,试验过程中在结构上安装上所有的测点(或者加上质量块),消除质量荷载的影响,来采集一组“一致”的数据。当然,有非常重要的一点要指出,由于附加质量的影响,我们已经改变了结构。但是,至少所有的数据将是一致的,不会因为质量荷载影响造成模态参数估计过程失真。
当然,真实结构具有各种测量问题,包括关于噪声、线性、时变等等方面。模态参数估计过程已经够复杂的了。不要让一些简单问题,比如质量荷载引起数据失真等,将这个过程进一步复杂化。我希望这个讨论让你明白了质量荷载和数据一致性为什么如此重要。如果你有关于模态分析的任何其它问题,欢迎垂询。
最新资讯
-
中汽中心工程院能量流测试设备上线全新专家
2025-04-03 08:46
-
上新|AutoHawk Extreme 横空出世-新一代实
2025-04-03 08:42
-
「智能座椅」东风日产N7为何敢称“百万级大
2025-04-03 08:31
-
基于加速度计补偿的俯仰角和路面坡度角估计
2025-04-03 08:30
-
《北京市自动驾驶汽车条例》正式实施 L3级
2025-04-02 20:23





 广告
广告





























































