模态空间—能否通过MAC判断振型正确与否？

MAC值怎样才算是好的？这样我就能判断振型正确与否了？
我们讨论一下这个问题。


作者：Peter Avitabile
翻译：德国M+P国际公司北京代表处

回答这个问题需要不少篇幅，很多人常常对MAC(模态置信准则)和其它相关分析工具感到困惑，为了澄清之前的一些错误看法，我们需要探讨以下问题。

为了便于讨论，我们假设有一个分析模型和相关的试验数据，从MAC（模态置信准则）和POC（伪正交性检查）的角度看，试验数据具有接近于理想的向量相关性，二者都接近于期望的单位矩阵。在向量相关程度很好的情况下，我们假定频率相关程度不高，并假定对第1阶模态有10%的频率误差，而对第2阶模态仅有1%的误差。那么，这种相关性意味着什么呢？

为了方便理解，我们来观察一个简单平板的响应，在之前的多篇模态空间文章中我们都曾讨论过它。图1显示了由随机激励作为输入激励引起的平板响应，以及由这个输入所引起的输出随机响应，同时显示出这种输入-输出现象的频域表示。


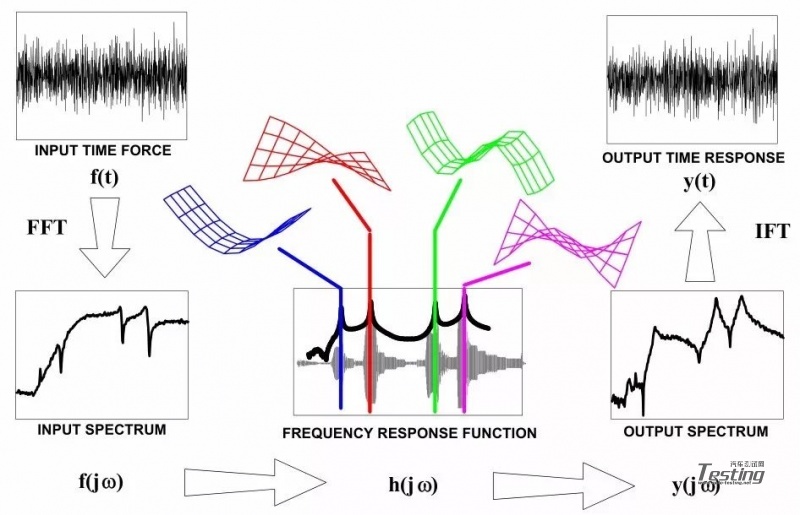
图1 随机输入下的总体响应示意图

FRF和脉冲响应不过是加到输入激励上的一种滤波器。图1显示了FRF以及各个固有频率上的相应模态振型，因此我们可以看出，频率和模态振型对确定系统的响应是非常重要的，不仅振型要正确，且频率误差也很重要。

如果频率值不正确，则响应将会改变，这取决于输入谱如何变化。在这种情况下，第二阶模态频率显示非常精确，同时输入谱在第2阶模态附近相当平坦，则轻微的频率改变只会引起少许的系统响应改变。

但是对于第一阶模态，频率会产生10%的误差，对于该阶模态，这个频率范围内输入频谱产生了明显的改变。所以与第二阶模态相比，频率误差对该阶模态更为重要。

所以现在来看很明显，MAC仅仅是向量相关性的一种指示。它只能确定向量相关与否，不能提供关于模型是否适合于精确地预测系统响应的任何信息。但向量如何会对响应产生影响呢？观察基本的运动方程是理解向量对响应产生影响的最好办法。

系统的物理响应是



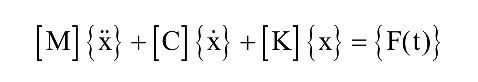
其中，[M]、[C]、[K]分别是质量、阻尼和刚度矩阵，与之一起的是相应的加速度、速度和位移，以及施加到系统上的力。在模态空间中，这可以写成


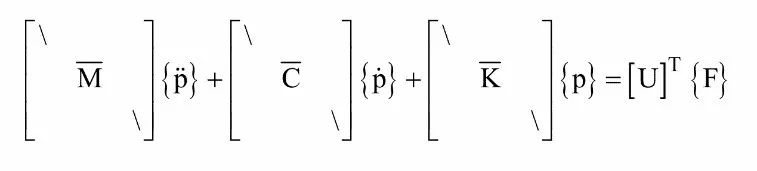
其中，对角矩阵是模态质量、模态阻尼和模态刚度，对应的是模态加速度、模态速度和模态位移。方程的右侧含有模态力，注意，利用模态向量的转置，这个力会被投影到模态空间。所以，模态振型对确定模态特性以及分配物理作用力到各个模态振子上是非常重要的。

如果模态振型发生改变，则载荷分配和响应也会改变。所以必须考虑将要如何利用这个模型，更重要的是，需要确定施加什么类型的载荷、什么响应对系统的总体性能产生影响的关键。在宽带、性质始终不变的随机激励条件下，这些影响通常会较小。

现在列举下一个例子，图2为一个正弦激励频率下含有多个谐波分量，注意该激励频率并没有位于系统的某一阶共振频率上。但是如果模型频率是错的，会是怎样的情况？实际上，该激励频率与第1阶模态频率相同，又会如何？那么这时，响应将会比我们预期的更大。


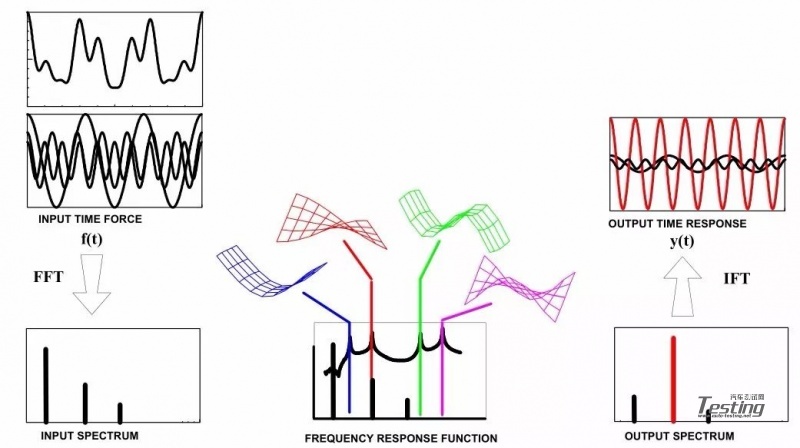
图2 正弦输入下的总体响应图

在另一方面，如果模型中第二阶模态频率错了的话，会发生怎样的情况？需注意的是，谐波驱动频率与系统的第二阶模态相同，由此可以预计对应的响应也是错误的。

那么，我们必须开始考虑MAC值对于整体模型和这个模型响应意味着什么？MAC（和POC）帮助我们确定振型的准确性，同时需考虑频响相关性以及激励函数。

因此在进行相关分析时，得到最佳的相关性是非常重要的。但这实际意味着什么呢？需要对预先设计的载荷引起的模型响应作一些评价，然后需要有人确定模型存在多大的变化量，以及它对于计算的响应会产生什么影响。一旦确定了模型中可接受的变化量，那么我们就能确定频率和模态向量的变化量。

我们需要认识到，没有一个模型是完美的。每个模型都会有误差，并且设计相同的载荷也会产生些许误差（如果考虑实际的载荷条件）。因此，在我们定义可接受的相关性大小之前，需要根据系统总响应级别定义哪些是可接受的。如果没有这样的规定，那么为频率相关性和MAC/POC相关性指定大小都毫无意义。对于判断模型预测的准确性而言，如果随意性地定义相关性，则不能发挥其最佳和全面的指示功能。

某些应用中，如果载荷对信号频率非常敏感的话，可能会有非常严格的要求，要求第1、2阶模态必须具有非常精确的频率相关性和振型相关性。在包含旋转设备的应用中，特定的工作速度对于系统总体响应非常关键。某些情况下，频率精度更为关键，而对于模态振型的相关程度要求不太严格。但另一些应用中，其中输入是均匀的宽带激励，则频率相关程度可能不太关键，而振型相关程度更重要。

基本事实就是，需要确定相关性和可接受的程度作为特定载荷参与下的系统详细分析的结果，不能简单地确定一个固定的相关程度指标。如果没有这种重要的评估，相关性就没有任何现实针对性。
当然，建立的模型满足相关性的一些基本标准，这是极佳的。但并不意味着这些一般的相关性水平得以满足，就一定会产生准确的结果。

我希望这个简短的讨论已经解释清楚了相关性分析的过程，以及为什么必须要在建立起跟系统响应关系的条件下，相关值分析才有效。如果您有其它关于模态分析的任何问题，欢迎垂询。