智能汽车横向控制方法研究综述

智能汽车在提高行驶安全性和减少交通事故方面有很大的优势，已成为世界范围内的研究热点。文章综述了智能汽车横向控制的国内外发展历程与研究现状；介绍了车辆横向动力学和轮胎力学的研究历程和模型；阐述了智能汽车横向控制理论和方法以及自动转向执行机构的设计；给出智能汽车横向控制研究的重点和发展趋势。

通过分析认为，系统非线性、不确定性和时变特性的智能汽车横向动力学建模和横向控制器设计，特别是高速时的横向控制，以及智能车辆感知决策系统与车辆本身系统的一体化设计，将是今后研究的重点。

本文来自 2017 年 6 月 15 日出版的《兵工学报》，作者是北京理工大学机械与车辆学院的陈慧岩教授、陈舒平和龚建伟副教授。

0. 引言

智能汽车（IV）是智能交通系统（ITS）的关键环节，作为减少交通事故，交通堵塞和环境污染等问题的有力手段，吸引了研究者的广泛关注。智能汽车涵盖了辅助驾驶、主动安全以及自主驾驶等各个方面，其发展的最终方向是自主驾驶。「自主驾驶汽车」是指使用计算机、传感器和其他技术和设备，使车辆在没有驾驶员的主动控制和连续监测下可以安全行驶的机动车辆 [1-3]。一些竞赛促进了智能汽车的发展，比如美国国防部先进项目研究局举办的 DARPA 挑战赛，韩国的 AVC 自主汽车竞赛和我国的智能汽车未来挑战赛等，目前的主要难点之一是确保高速时的自主驾驶 [4]。

行驶控制是智能车辆研究领域中的核心问题之一，指根据当前周围环境和车体位移、姿态、车速等信息按照一定的逻辑做出决策，并分别向油门、制动及转向等执行系统发出控制指令 [5]。智能汽车的行驶控制主要包括纵向控制和横向控制：

纵向控制是指调整车速使车辆间保持足够的空间，使用最少的制动保持相对恒定的车速，并在紧急情况下尽可能快的制动 [6]；
横向控制是指路径跟踪，即通过自动转向控制使车辆始终沿着期望路径行驶，同时保证车辆的行驶安全性和乘坐舒适性 [7]。

由于汽车是一个强耦合变参数的非线性系统，汽车的纵向运动和横向运动存在很强的耦合关系 [8]，耦合效应包含 3 类：运动学耦合、轮胎力耦合以及载荷转移耦合：

对于运动学耦合效应，例如转向轮的侧偏力，实际在纵向有一个分量，从而影响纵向加速度，又如横向离心力是纵向速度和曲率的函数；
轮胎的侧偏力与纵向力也是相互耦合的，对于给定的轮胎路面摩擦系数，作用在每个轮胎上的侧向力和纵向力相互限制，使合力不会超过附着极限 [9-11]；
载荷转移也有显著的耦合效应，当载荷转移是由纵向加速度引起时，前后轮胎的垂直载荷重新分配将对横向动力学产生很大的影响 [9-11]。

一些学者专门研究了二者间的耦合性问题，例如，Lim 等明确了各种耦合效应的特征，设计了一种联合控制器来补偿这些效应 [11]。本文侧重阐述智能汽车横向控制的相关研究内容。

1. 摇智能汽车横向控制的发展历程

根据环境感知传感系统的不同，智能汽车横向控制可分为非前瞻式参考系统和前瞻式参考系统 [6,12]：

非前瞻式参考系统通过计算车辆附近的期望道路与车辆之间的横向位置偏差来控制车辆实现道路跟踪，例如安装在道路中间的电缆或磁道钉参考系统 [12-13]。
前瞻式参考系统通过测量车辆前方的期望道路与车辆之间的横向位置偏差来控制车辆实现自动转向，类似于驾驶员开车行为，例如基于雷达或机器视觉的参考系统 [12]。

横向控制研究最初是由美国通用汽车公司和美国无线电公司在 20 世纪 50 年代末合作开展的，目的是为解决自动化公路系统（AHS）车辆自动驾驶问题。从那时起，美国本土和海外的研究者对 AHS 的各方面进行了研究，比如美国国家自动化公路系统联合会、日本智能交通系统、美国加利福尼亚州的公路先进技术（PATH）项目 [13-14]。其中，美国俄亥俄州立大学在美国运输部的资助下从 1964 年到 1980 年间进行了广泛研究，车辆的横向控制是其主要研究方向之一 [14]。美国加利福尼亚州的 PATH 项目比其他项目更加强调自动车辆控制技术，其横向控制注重车辆和道路间合作的理念，智能车辆所需的大量信息由安装在道路上的特殊单元发送，该方法比依赖视觉系统观测现有车道标线的完全自主车辆的概念更简单经济 [15]。 PATH 项目的横向控制问题从 1988 年开始研究，主要工作包括建模、控制器设计、开环仿真、闭环仿真、开环实车试验和闭环实车试验 [16]。

在文献 [17] 中，20 世纪 70 年代，Fenton 等用经典控制理论设计控制算法，并进行了试验验证。随后在 1988 年，Fenton 等基于前瞻式参考系统，通过测量车辆前方的横向偏差，使用最优控制技术和观测器设计了全状态反馈，在实验室中用模拟计算机仿真车辆动力学，并对结果进行了评价 [18]。两种设计都使用了反馈控制器，依赖反馈控制的抗干扰能力来跟踪道路曲率。20 世纪 80 年代，Ackermann 应用参数空间鲁棒控制方法设计自动转向控制器。通过对车辆质量分布的假设，系统的阶数从 4 阶降到 3 阶，从而减小了鲁棒控制器设计的难度。鲁棒反馈控制既可以满足直线跟踪也可以满足车速，载荷和路面条件等参数变化的曲线跟踪[17]。但是，Ackermann 对向心力的处理不准确，应谨慎看待其结果。

在文献 [12] 中，1990 年到 1991 年间，Peng 等提出自动转向前馈-反馈控制算法，前馈控制量是由道路曲率计算的稳态前轮偏角或预瞄前轮转角，反馈控制算法采用频率线性二次型（FSLQ）最优控制理论来设计，考虑跟踪误差的同时也保证了车辆乘坐舒适性 [19]。1991 年，Hessburg 等基于非前瞻式参考系统，研究了使用前馈-PID 反馈控制算法和离散磁道钉参考系统进行实车横向控制的可行性 [20]。1992 年到 1993 年间，Peng 等通过实车试验验证了上述两种控制算法的道路跟踪精度，结果表明以 50 km/h 的车速，跟踪半径为 75 m 的 1/4 圆弧时，最大横向偏差小于 10 cm，在一些恶劣工况下也不超过 15 cm，但车速高于 50km/h时，跟踪精度大于 25 cm 而达不到性能要求，此时必须引入以预瞄控制为基础的前馈控制量 [16]。因此，Peng 等提出了自动转向预瞄控制算法 [21]，即采用预瞄距离内的道路曲率信息来计算前馈控制量。1999 年，Tan 等基于非前瞻式参考系统，设计了考虑车辆参数变化的鲁棒横向控制器 [22]。

美国在面向非结构化环境下的智能车辆技术也展开了研究。在文献 [23] 中，2002 年，Kato 等基于差分全局定位系统的航迹推算功能设计了横向控制算法，车辆由包含一系列路点的精确地图引导 [24]。2003 年，Hernandez 等使用 GPS 从数字地图中提取地理信息来修正非前瞻式参考系统的控制器，提高了道路跟踪的精度 [25]。

DARPA 挑战赛极大地推动了横向控制技术的发展。2005 年，美国斯坦福大学参赛的智能车 Stanley 基于车辆-道路几何关系设计了自动转向控制器，该控制器由前轴处的方向偏差和横向位置偏差两部分组成，并通过比例增益来调节不同车速下的控制律 [26]。2007 年，美国卡内基梅隆大学参赛的智能车 Boss 采用综合了任务规划、行为规划和运动规划的 3 层规划系统，在城市环境下行驶车速达到 48 km/h [27]。

2008 年，Besselmann 等提出混合变参数的模型预测控制，应用于自主车辆转向控制，对比了基于非线性和线性预测模型设计的控制器性能 [28]。

在文献 [12] 中，2009 年，Kritayakirana 等开发了基于 Audi TTS 原型车的智能车辆平台，以实现车辆极限工况下的自主驾驶。该平台的自动转向控制采用前馈-反馈控制，前馈量由期望道路曲率直接计算得出，而反馈量由两部分组成，一个是由偏离车道的位置偏差计算，另一个是以保证车辆横摆运动收敛来计算 [29]。

2014 年，Hindiyeh 等提出一种使后轮驱动车辆在后轮摩擦力饱和时，能自主地稳态转向的控制方法。该控制器基于循环嵌套结构，在外循环，横摆角速度作为侧偏动力学的合成输入；在内循环，用轮胎力对横摆角速度动力学进行反馈线性化 [30]。

2015 年，Hong 等提出了一种使车辆转弯时侧倾运动最小化的模型预测控制方法。该路径跟踪控制策略考虑了侧倾运动，用滚动最优控制技术将转弯时的侧倾最小化，能预先对车辆将产生的侧倾运动做出反应 [31]。

2016 年，Wang 等采用主动前轮转向和直接横摆力矩共同控制的方法研究了四轮独立驱动自主车辆的路径跟踪控制问题，提出了一种改进的合成非线性反馈控制策略来提高瞬态性能，消除路径跟踪控制的稳态误差 [32]。

随着计算机技术的飞速发展，软计算技术被应用在自主车辆的控制上。模糊逻辑控制为车辆自动转向控制提供了一个考虑驾驶员经验和工程判断的平台 [23]。1991 年到 1994 年间，Hessburg 等基于非前瞻式参考系统，使用模糊逻辑控制器研究了车辆横向控制，在全尺寸车辆上实施了人工调节的模糊控制器，其包含 3 部分模型：反馈、预瞄和增益调节 [33]。

我国智能车辆技术的研究起步较晚，与发达国家有一定差距。目前从事这方面研究工作的高校和单位主要有国防学技术大学、北京理工大学、上海交通大学和吉林大学等，以追踪国外研究水平为主，近些年的研究成果有：

文献 [34] 提出将变论域模糊控制、自适应技术和H肄最优控制理论相结合实现对自主汽车的侧向系统进行控制，提高了系统的鲁棒性和控制精度。
文献 [35] 针对非完整运动约束车辆，利用反馈线性化方法设计了轨迹跟踪器，仿真研究了跟踪算法的鲁棒性。该文献指出预瞄在高速自主车的轨迹跟踪中起着举足轻重的作用，将预瞄与反馈线性化方法相结合是下一步系统设计的一个方向。
文献 [36] 基于单点预瞄最优曲率模型设计侧向加速度 PD 跟踪控制器，联合车-路横向动力学模型构建横向控制闭环系统，设计模糊控制器对预瞄距离进行模糊选择，以提高车辆横向控制精度和减小侧向加速度，采用遗传算法对模糊规则进行优化以使横向控制系统性能达到最优。

2. 智能汽车整车动力学建模和控制

智能车辆横向控制的设计有两种方法：一种是基于模仿驾驶员行为，另一种是基于车辆动力学模型和控制理论。前一种方法不需要车辆动力学的精确知识，仅需要一个表达响应特性的车辆模型和一个模拟驾驶员行为的控制器。后一种方法通常需要一个较好的车辆动力学模型，然后用不同的控制算法来达到特定目标 [19]。本文主要讨论基于车辆动力学模型的控制理论和方法。

2.1 智能汽车整车动力学建模方法

无人驾驶智能汽车整车动力学的建模是以有人驾驶车辆动力学理论为基础，历史上车辆动力学研究有几个重要人物：

20 世纪 30 年代初，Maurice Olley 最早提出操纵动力学理论，试图解决行驶平顺性和操纵稳定性之间的协调关系；
20 世纪 30 年代 ~ 20 世纪 50 年代，Cough 等研究了轮胎特性并定义了侧偏角、不足转向和过度转向的概念；
20世纪 50 年代以后，Segel 提出了 3 自由度操纵动力学方程：在侧向、横摆基础上增加了侧倾运动，扩展了操纵动力学的分析内容，形成了一套较为完整的关于操纵和转向的基础理论体系 [37]。

2.1.1 2 自由度整车模型

在文献 [38] 中，20 世纪 40 年代，Riekert 和 Schunck 建立了最早的 2 自由度车辆动力学模型。他们将整车看作是一个刚体，考虑了前后轴侧偏刚度，对左右两侧的车轮不进行区分，车轮转角直接作为模型的输入，定义了汽车的不足转向和过多转向特性。

文献 [39] 采用了单轨 2 自由度模型，模型忽略了车辆的垂向运动、俯仰运动、侧倾运动以及悬架运动，轴荷侧向转移、空气动力学载荷和转向几何，假设道路的超高和坡度，整车侧偏角和横摆角偏差都很小。研究表明在侧向加速度小于 0.2g 的工况下，采用线性轮胎的传统 2 自由度「自行车冶模型」是完全够用的，使用这种低阶模型设计的控制器也表现良好。

文献 [40] 采用了考虑纵向车速的单轨模型。文献 [41] 采用考虑纵向车速的双轨模型来描述车辆稳定性到极限时的动力学特性，建立了具有自适应功能的非线性观测器来估计整车质心侧偏角。

2.1.2 3 自由度模型

文献 [42] 描述了 Segel 的 3 自由度模型。基于 Milliken 的设想：在建立车辆的数学模型时，可将车辆当作一个线性的动力学系统，Segel 建立了包含横摆运动、侧向运动和侧倾运动的 3 自由度车辆模型来描述转向响应，研究表明该假设对于合理范围的侧向运动分析是可行的。

文献 [43] 描述了 Nalecz 的 3 自由度模型，通过考虑悬架侧倾中心高度和整车侧倾轴线的变化分析了悬架运动学和动力学对车辆转向响应的影响。文献 [44] 基于 Segel 模型建立了 3 自由度模型，通过分析特定路面输入的动力学方程，研究了恶劣路面上车辆的侧倾、侧向及横摆响应特性，并进行了舒适性评价。

2.1.3 7 自由度模型

文献 [45] 采用魔术公式轮胎模型建立了非线性 7 自由度车辆模型，包括 4 个车轮的转动，车辆的纵向运动、侧向运动和横摆运动，研究了后轮转向系统对车辆操纵稳定性的影响。文献[46]采用非线性 7 自由度车辆模型和 Dugoff 轮胎模型对车辆过激励时的控制器进行设计和仿真，并使用线性 2 自由度模型对鲁棒性进行评价。

2.1.4 8 自由度模型

文献 [39] 建立了 8 自由度车辆模型，包含 4 个车轮的转动，车辆的纵向运动、侧向运动、横摆运动和侧倾运动。文献 [47] 分别在横摆平面和侧倾平面建立动力学方程，建立了非线性 8 自由度整车模型，轮胎采用了魔术公式模型。

2.1.5 12 自由度模型

在文献 [38] 中，郭孔辉院士为分析汽车在转弯制动工况下响应，建立了 12 自由度模型，分别是簧载质量的 6 个自由度、两侧车轮绕主销转动自由度以及 4 个车轮的旋转自由度。轮胎模型计算了侧偏纵滑联合工况下的力学特性，悬架模型则对杆件产生的运动学约束关系进行了详细推导。

2.1.6 17 自由度模型

在文献 [38] 中，Garrot 等建立了 17 自由度模型，该模型对轮胎、悬架的非线性特性进行了充分描述，能够进行汽车侧翻、汽车稳定性、正弦扫频、极限操纵性和转弯制动等多种工况的仿真。

2.2 轮胎力学模型

车辆所受到的控制和扰动力，除了空气动力以外，其余均来自轮胎与地面的接触区域。车辆依靠轮胎与地面的相互作用产生各种运动，因此轮胎对于车辆动力学和控制非常重要 [48]。

2.2.1 轮胎动力学研究的发展历程

轮胎动力学特性的研究可以追溯到 20 世纪 30 年代，在文献 [49] 中，Bradley 和 Allen 在 1931 年研究了汽车轮胎动力学特性。1937 年，Koesler 和 Klaue 通过试验发现制动力是纵向滑移率的函数。1953 年，Wilkinson 的研究表明橡胶在冰路面的摩擦系数随着载荷的增加而下降，并在某个车速下有最大值。1958 年，Schallamach 研究证明了橡胶的摩擦系数在某个车速下的最大值取决于温度。Nordeen 和 Cortese（1963 年）、Krempel（1965年）和 Henker（1968 年）的研究表明，侧向力和回正力矩的变化与制动力和牵引力的变化有着函数关系。

轮胎侧偏特性最初的理论研究是由 Fiala 在 1954 年开展的。他假设胎面的侧向位移仅在轮胎接地面产生，将轮胎模型简化为受侧向集中载荷作用的弹性支撑梁，推导了基于固定侧偏角的侧向力和回正力矩表达式。Bergman 在 1961 年通过引入弹簧相互作用的概念最先对制动时的侧偏特性开展了研究。随后他和 Beauregard（1974 年）研究了影响车辆转向响应特性的稳态和瞬态轮胎特性 [49]。

Dugoff 等在 1970 年将轮胎路面的摩擦系数表达为胎面的滑移速度、零滑移时的摩擦系数和摩擦损失因子的函数。Nguyen 和 Case 在 1975 年研究了之前建立的摩擦模型，并指出了相同点和不同点，他们通过模拟在转弯、直线制动和转弯制动下的简单非线性车辆模型，研究了车辆对于不同类型轮胎的响应敏感度，得出 Dugoff 的轮胎模型是支持试验数据的，并强调了摩擦椭圆概念的重要性 [49]。

Bernard 等在 1977 年建立了用于纵滑和侧偏的联合工况半经验轮胎模型，该模型适用于带束层轮胎、子午线轮胎、斜交帘布层轮胎的剪切力特性。Pacejka 在 1979 年研究了描述轮胎稳态转向特性的数学模型，并给出了反映轮胎、悬架和转向特性综合作用的等效轮胎侧偏特性的概念。基于试验研究，Bakker 等在 1987 年研究建立了解析表达式来描述轮胎侧向力、制动力和回正力矩的特性。虽然这些方程仅限于纯侧偏或纯制动下的稳态工况使用，但是为制动转向联合工况下的轮胎模型提供了基础。随后，Bakker 和 Pacejka 等分别于 1987 年、1989 年和 1991 年在试验研究的基础上总结出描述轮胎侧向力，制动力和回正力矩的解析表达式，建立了著名的「Magic Formula 冶模型」[49]。

在文献 [50] 中，郭孔辉院士自 1983 年以来在轮胎力学特性方面也作了很多的理论与试验研究工作。他以 Fiala 的理论为基础，通过试验建立了侧偏力与回正力矩的半经验模型，该模型中的侧向力表达式后来被改进为双指数模型。1990 年，他从胎体的一般变形模式和垂直载荷分布的一般模式出发，推导出侧向力与回正力矩的一般表达式，在此基础上又获得了侧偏与纵滑联合工况下的理论模型以及一种便于进行汽车转向、制动与驱动的动态仿真统一模型。

相对稳态侧偏特性研究而言，非稳态侧偏特性的研究尚不成熟，关于轮胎的非稳态侧偏特性，最先是为了研究轮胎摆振问题。1941 年 Dietrich 将轮胎看成是无限长的「弦」，首先提出了接地印迹的运动方程；1966 年 Pacejka 为了研究摆振，将弦模型加以发展推导出 Pacejka 摆振模型，1981 年对该模型进行了综合与整理，得到了以轮胎弦模型为基础的轮胎非稳态侧偏模型；Loeb 等在 1990 年研究了轮胎的侧向刚度、侧偏刚度和松驰长度之间的关系；Bernard 等在 1995 年研究了侧偏角与纵滑率的瞬态延迟特性；1997 年 Mastinu 等利用胎体梁模型并结合有限元模型推导了轮胎瞬态特性的半理论模型 [50]。

国内对轮胎非稳态侧偏特性的理论研究主要有：

1993 年，孙逢春等以 Willumeit 的「胎带-胎冠-轮辋」模型为基础，将其推广到动态范围；
1996 年，郭孔辉等从胎面印迹的侧向变形和胎体的侧向平移变形出发，在考虑胎宽影响的条件下，根据轮胎接地印记变形的几何关系和接地点瞬时位置关系，得出胎面的侧向与纵向瞬时变形表达式，考虑胎体的复杂变形后，模型能真实地反映轮胎的力学特性和物理实质，使得理论模型与试验结果更加吻合 [50]。

2.2.2 摇常用轮胎模型

1）Dugoff 轮胎模型

当仅研究低侧向加速度下的横向动力学时，线性侧向轮胎模型可以给出较好的结果。但当纵向和侧向均发生滑移，如自动紧急操纵，或者当侧偏角很大时，轮胎力在摩擦极限达到了饱和。Dugoff 等基于摩擦椭圆的概念建立了非线性轮胎模型，可以用来说明这两种作用。Dugoff 的轮胎模型被广泛应用于非线性仿真 [39,51]。

2）Magic Formula 轮胎模型

Pacejka 的魔术公式是在车辆动力学研究中，广泛用于计算稳态轮胎力和力矩特性的半经验轮胎模型 [52]，对于给定垂直载荷和外倾角的魔术公式一般形式 [53]：



3）Burckhardt 轮胎模型

与魔术公式轮胎模型相比，Burckhardt 轮胎模型表达式更加简单，二者均准确捕捉了轮胎的关键性能。由于实际中轮胎的侧偏刚度受很多因素影响，比如轮胎路面附着系数、轮胎垂直载荷、车轮纵向滑移、轮胎充气压力、轮胎磨损等，Burckhardt 轮胎模型并非在所有情况下都准确，但调教简单方便，因此可实现实时仿真 [54]。

4）LuGre 轮胎模型

LuGre 轮胎模型考虑了主要静态现象，比如黏附性、动摩擦、黏性摩擦以及一些动态现象，比如零滑移时的位移和迟滞 [55]，能较准确地描绘大部分静态和瞬态摩擦力行为。该模型虽然简单，但包含了反馈控制所关注的大部分摩擦现象。低速时的摩擦特性对良好的转向性能和跟踪效果尤其重要，该模型能描述任意稳态的摩擦特性，支持轮胎摩擦迟滞引起的滞后现象，黏附性中的弹簧弹性现象。所有这些现象都统一到 1 阶非线性微分方程中，便于摩擦系统的仿真 [56]。

2.3 智能汽车横向控制方法

2.3.1 经典控制方法

经典控制理论是建立在频率响应法和根轨迹法基础上的理论，是以拉普拉斯变换为数学工具，以单输入单输出的线性定常系统为主要的研究对象。

1991 年，文献 [20] 研究了前馈-PID 反馈控制算法的横向控制。前馈控制循环利用磁道钉提供的位置、方向、弯道信息，将稳态前轮转角加入到 PID 反馈控制环节中，并表示为曲率半径的函数。

1998 年，文献 [57] 指出在自动转向车辆中，通过横摆角速度反馈将横摆运动和横向运动解耦是经常用到的控制方法。研究表明使用动态前视和横摆角速度反馈的两种方法，通过极点消除、零点补偿，都能使横摆运动解耦，但二者在系统极点或零点是否重新配置上不同，动态前视的解耦控制方法将系统的零点重新定义为开环系统的极点；而横摆角速度反馈的解耦控制方法将闭环系统的极点移至开环系统的零点。

2011 年，文献 [58] 基于单轨线性 2 自由度整车模型，提出了一种由期望航向偏差生成器和鲁棒 PID 反馈控制器组成的横向控制系统。该系统给出了不同车速范围的 PID 控制参数，具有较好的跟踪性能。

2011 年，文 [59] 使用嵌套 PID 转向控制来进行自主车辆的路径保持。该控制策略包含两个嵌套的控制块 C1 和 C2，C1 在恒定干扰和参数不确定下基于横摆角速度偏差跟踪横摆角速度，C2 基于车辆前方预瞄位置与道路中心线的横向偏差，生成横摆角速度参考信号，使横向偏差趋于零期望值。上述文献 [20，57-59] 所采取的控制器方框图如表 1 所示。



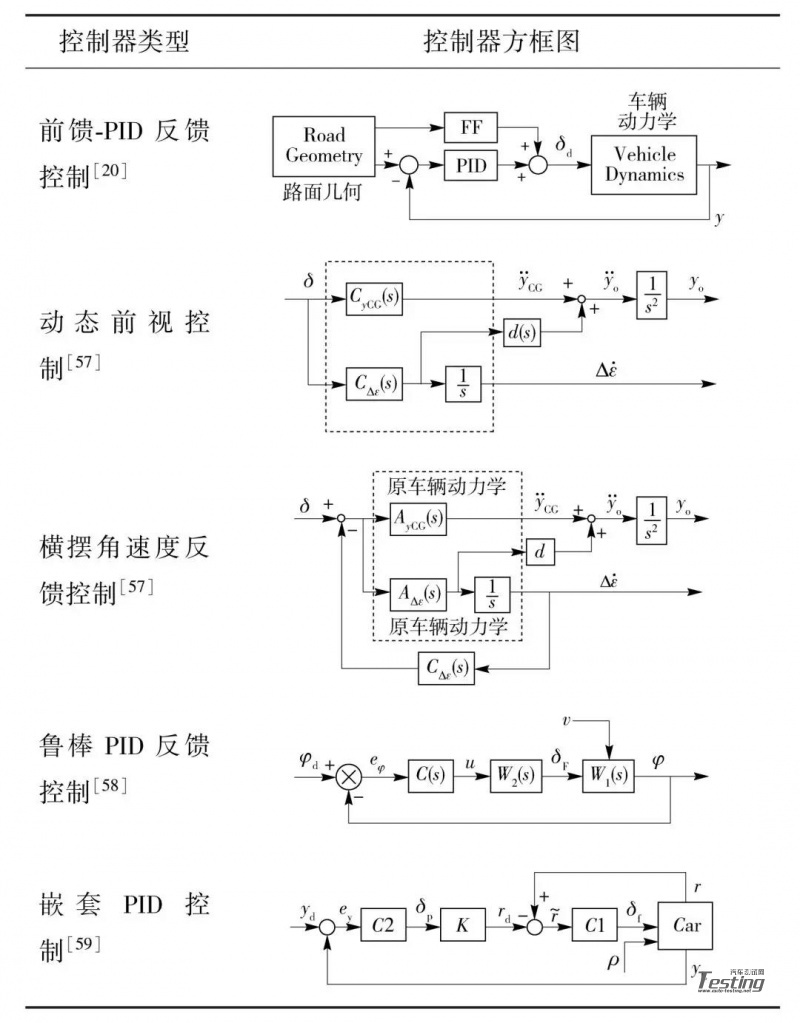
表 1 经典控制理论

虽然经典控制理论在工程上应用广泛，但具有明显的局限性，特别是难以有效地应用于多变量系统和时变系统，也难以揭示系统更深刻的特性。

2.3.2 最优控制方法

最优控制理论是在给定限制条件和性能指标下，寻找使系统性能在一定意义下为最优的控制规律。最优跟踪控制指的是基于最优化原理建立的反馈控制方法。

1988 年，文献 [18] 根据 Bonderson 提出的最优横向控制律，选择反馈控制律的指标，并得出求解线性调节问题的 Riccati 代数方程，设计了速度适应的全状态反馈的横向控制器来满足横向位置跟踪精度、鲁棒性和乘坐舒适性的要求。

在文献 [60] 中，2006 年，马莹等提出了有限时间最优预瞄横向控制算法，根据车道保持控制系统需要较高实时性的要求，使用了同时考虑车辆当前偏差、预瞄点偏差和控制变量的有限时间二次型性能指标函数，运用最优跟踪算法设计了最优预瞄控制器，仿真和试验结果表明该算法具有较好的跟踪效果 [61]。

上述最优控制方法虽然能在一定条件下取得不错的控制效果，但控制模型参数的不确定性，如轮胎的侧偏刚度等，以及外界干扰的不确定性没有考虑。因此，为了减小不确定性因素对系统控制性能的不利影响，又发展了两种控制方法：一种是自适应控制，另一种是鲁棒控制。

2.3.3 自适应控制方法

自适应控制是指随时辨识系统的数学模型并按此模型去调整最优控制规律。其基本思想是，当被控对象内部的结构和参数以及外部的环境干扰存在不确定性时，在系统运行期间，系统自身能对有关信息实现在线测量和处理，从而不断地修正系统结构的有关参数和控制作用，使之处于所要求的最优状态，得到期望的控制结果。

在文献 [60] 中，2004 年，Netto 建立了包含道路曲率和横向风阻变化引发摄动的车辆动力学模型，提出了基于视觉的智能车辆横向自适应控制器，并通过仿真检验了该控制算法的有效性 [62]。

2016 年，文献 [63] 提出一种新的输出约束控制器来控制路径跟踪中的横向偏差和轮胎滑移时的横向稳定性。为了消除系统参数不确定性的影响，同时考虑车辆的横向稳定性，采用自适应和鲁棒的线性二次型控制器来获得最优的主动前轮转角和直接横摆力矩。

2.3.4 鲁棒控制方法

控制系统的鲁棒性一般是指系统在它的参数或结构发生摄动时保持某种原有品质的能力。鲁棒性包括鲁棒稳定性和鲁棒性能 [48]。

2004 年，文献 [64] 基于简化的两轮摩托车模型，提出一种横向鲁棒控制器设计方法，给出了道路曲率的平滑算法及闭环系统的仿真结果，并进行了跟踪误差分析，考虑了参数变化所导致的模型不确定和外界干扰引起的不确定性。

2016 年，文献 [65] 提出了一种新的基于轨迹跟踪误差的鲁棒控制方法。通过结合前馈和鲁棒控制策略，设计了线性模型预测控制器，使直线和曲线的跟踪误差均满足要求。

2016 年，文献 [66] 为了解决自主地面车辆路径跟踪时延迟和数据丢失的问题，提出了一种鲁棒H肄状态反馈控制器来实现路径跟踪和横向控制。为提高控制器的鲁棒性，考虑了轮胎侧偏刚度和外界干扰的不确定性。

2.3.5 滑模控制方法

滑模控制（SMC）本质是一类特殊的非线性变结构控制，是由前苏联学者 Utkin 等于 20 世纪 50 年代提出的，其非线性表现为控制的不连续性。这种控制策略的特点在于系统的「结构」并不固定，可在动态过程中，根据当前的状态有目的地不断变化，迫使系统按照预定的「滑动模态」的状态轨迹运动。由于滑动模态可以进行设计且与对象参数及扰动无关，SMC 具有响应快速、对参数变化及扰动不灵敏、控制动作简单可靠等优点 [48]。

2011 年，文献 [67] 基于 2 自由度单轨非线性模型，采用滑模变结构控制理论，设计了基于趋近律的自动转向控制算法，分析了趋近律函数的指数趋近项参数和等速趋近项参数对系统输出的影响，并根据侧向加速度的要求提出了参数选取方法。仿真结果表明，该控制算法在高速路径跟踪时，具有良好的道路跟踪精度及动态性能。

2012 年，文献 [68] 基于 7 自由度非线性车辆动力学模型，设计滑模控制器跟踪期望横摆角速度，使车辆稳定地跟踪目标路径。仿真和试验表明路径跟踪偏差随着车辆速度及道路曲率的变化波动范围较小，具有较好的鲁棒性和自适应性。

2016 年，文献 [4] 比较了 3 种横向非线性自适应控制器：高阶滑模控制器、基于侵入与不变原理的控制器、基于无源输出反馈的自适应 PI 控制器。3 种非线性控制器对于车速和道路曲率变化下的路径跟踪都具有较好鲁棒性。其中，SMC 的稳态偏差较低，但对于高速时的道路曲率突变很敏感，该滑模控制系统仅在滑动阶段对干扰不敏感，对滑模到达前较敏感。

2.3.6 模型预测控制方法

模型预测控制（MPC）也叫做滚动时域最优控制，该控制器考虑控制系统的非线性动力学模型并预测未来一段时间内系统的输出行为，通过解决带约束的最优控制问题使得系统在未来一段时间内的跟踪误差最小 [69]。这种方法鲁棒性较强，能在线处理约束并使其动态得到满足；对非线性动态的考虑也相当方便———采用非线性模型来预测未来动态 [70]。

2012 年，文献 [71] 提出了对自主和半自主地面车辆的分层控制框架。上层路径规划基于由 4 轮非线性整车模型建立的运动基元，下层控制使用非线性模型预测控制器跟踪规划路径。所提的控制策略在结构化环境下，选择可行的运动基元比使用实时非线性优化更快。

2015 年，文献 [72] 基于试验数据，比较了运动学和动力学 2 自由度模型预测车辆未来状态的误差。动力学模型采用线性轮胎描述轮胎路面间的作用，并基于运动学自行车模型设计了自主车辆 MPC 控制器，仿真和试验结果验证了在有风道路和不同车速下该控制算法的有效性。



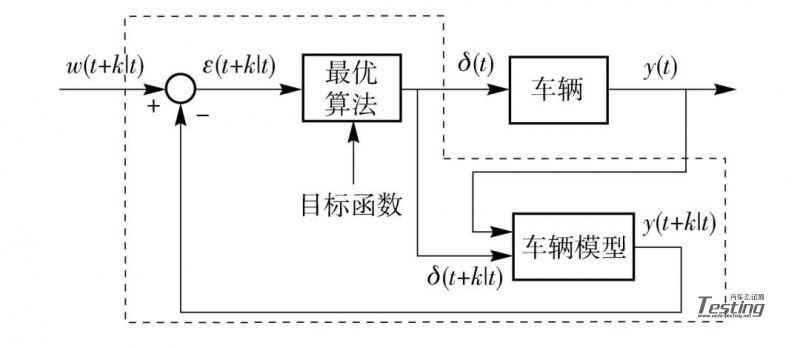
图 1 模型预测控制

2015 年，文献 [73] 采用 2 自由度自行车模型和魔术公式轮胎模型，对自主车辆的自动转向控制提出了一种非线性模型预测控制（NMPC）方法。该 MPC 控制包含两个部分：控制系统的数学模型和最小化目标函数的最优算法，在每个采样时间 t，控制器通过车辆模型预测未来车辆的横向位置 y(t+k|t)，转角控制信号 δ(t+k|t)通过求目标函数极值获得，目标函数定义为系统输出尽可能接近期望横向位置 ω(t+k|t)，并满足预先定义的约束。δ(t)=δ(t|t)和y(t)=y(t|t)分别表示实际前轮转角输入和车辆横向位置，如图 1 所示。

2.3.7 模糊控制方法

模糊控制是以模糊数学理论，即模糊集合论、模糊语言变量及模糊逻辑推理等作为理论基础，以传感器技术、计算机技术和自动控制理论作为技术基础的一种新型自动控制理论和方法。模糊控制器的基本结构主要由模糊化、知识库、模糊推理和清晰化等4部分组成，如图 2 所示。

1994 年，文献 [33] 设计模糊逻辑控制器（FLC）控制车辆的横向运动。FLC 的结构基于反馈、预瞄和增益调节规则来建模。FLC 的参数使用了驾驶员的操纵特性和现有控制器信息，模糊预瞄规律使用前方道路曲率半径的信息，增益调节规则基于车速选择合适的控制器。试验结果表明，采用 FLC 的横向跟踪效果与采用 FSLQ 控制器和PID控制器水平一样。

2011 年，文献 [74] 提出一种自动调节的模糊控制器来控制无人驾驶车辆的转向，为达到这个目的，实施了带约束的迭代遗传算法，该算法能够迭代调整模糊控制器的隶属函数和规则库。

3. 横向控制执行机构设计

智能汽车横向控制执行机构由传感器、控制器、执行器 3 部分组成，主要任务是通过信号采集和系统控制，控制电机准确转动前轮，使其偏角到达期望位置。传感器主要采集用于电机控制的信号，如前轮偏角、前轮偏角变化率、电机转速、电机相电流等，并传输给电力控制系统控制器，电力控制系统控制器根据期望值和当前值反馈控制占空比实现对电机的位置控制，执行机构则把电机的转动传递到前轮的转动 [12]。

文献 [22] 基于磁道钉自动公路系统，介绍了 PATH 项目和通用汽车萨吉诺转向部门合作开发的自动转向控制系统的组成和设计方法。转向执行机构通过安装在转向管柱上端的附加无刷直流电机工作，已有的液压助力系统作为转向助力，其目标是控制伺服根据指令不断调整车轮的转角，使汽车保持在正确的轨迹上。

文献 [75] 介绍了美国弗吉利亚理工大学的 CALVIN 智能车设计方法。该车转向系统采用集成了位置反馈的 12V 直流线性执行机构，替换了原车齿轮齿条转向器。电机由脉冲宽度调制信号（PWM）来控制。控制器的输入信号可以由自主驾驶模式下的微控制器生成，也可以由手动模式下的无线电控制接收机发出。

文献 [76] 介绍了无人驾驶智能电动车平台的设计方法，包括各个电力控制执行机构的设计，并使用无人驾驶控制算法验证了该智能车平台的性能。该转向控制模块采用电动助力转向系统（EPS），使用 24 V、420 W 的伺服电机实现操纵，EPS 的控制基于 RS-232c 标准串口进行，同时包含一个测量方向盘转角的传感器，并通过CAN总线进行通讯。

文献 [77] 介绍了无人驾驶方程式赛车的线控系统设计和实现，其设计思想是使线控转向系统能够像驾驶员那样操纵汽车。该系统通过集成了减速器的 12 V 电机，电机和转向系统之间通过皮带轮传递运动，来完成汽车的转向操纵，安装支架提供了张紧功能。

文献 [78] 提出了一种用于自主驾驶汽车U型转弯的横向控制模块，该转向系统通过安装在转向柱上的执行机构和减速齿轮机构实现转向操纵，执行机构通过皮带轮传递力矩。控制器读取 CAN 总线发来的电机转速和位置信息，然后基于 RS232 发出期望的转向 PWM 信号。

4. 总结和展望

智能汽车横向控制从 20 世纪 50 年代开始研究并持续到现在，控制方法先后经历了经典控制、现代控制和智能控制。本文结合国内外发展状况，阐述了智能汽车横向控制的研究历程，介绍了车辆横向动力学的建模和常用的轮胎模型，接着阐述了智能汽车横向控制的理论和方法，并对横向控制执行机构的设计进行了说明。智能汽车横向控制今后的研究重点将集中在：

1）整车动力学建模。虽然 2 自由度模型在轮胎侧偏角较小时能较好地模拟车辆侧向和横摆运动特性，但当侧偏角较大时，需要考虑轮胎的非线性特性，建立更高自由度的车辆动力学模型，同时也要考虑自由度的增加对实时性的影响。因此，整车动力学建模将是横向控制研究的一个重点。

2）考虑车辆非线性、不确定性和时变特性的横向控制器设计。在各种控制方法中，采用智能控制和其他控制相结合的方法将是今后智能汽车横向控制研究的热点，对于复杂模型中参数的不确定性和时变特性，整车参数估计、运动状态估计也是横向控制研究的重点。

3）自动制动的同时紧急转向回避条件下，智能车辆纵向、横向耦合控制的研究。在紧急工况下，转向避让是驾驶员的一种自然反应，当通过制动无法避免碰撞时，往往还可以通过转向进行避撞。智能汽车也应该在紧急情况下，自动制动的同时考虑转向回避控制，以满足未来汽车安全控制的需要。行驶的汽车是一个复杂的强耦合、变参数的非线性系统，其纵向、横向运动是相互耦合、相互影响的，特别是车辆在不平路面上高速行驶时，其耦合特性更加明显。以往车辆的纵向、横向控制是通过两个独立的控制器完成的，没有考虑耦合影响，这导致控制器误差偏大，影响控制精度。因此，分析在自动制动的同时，紧急转向回避条件下，智能车辆纵向、横向运动的耦合控制将是智能汽车运动控制研究的一个重点。

4）智能汽车一体化设计。传统的无人驾驶汽车大多采用加装执行机构的方式改造车辆的转向系统，这种方法存在诸多弊端：该方法将上层决策系统的指令施加于外部机构，有可能导致附加控制系统和原车控制系统不能合理地兼容，难以达到预定的控制效果。而且，外加机构的安装减少了汽车的空间，增加了环节和控制的复杂性及成本，并降低了无人驾驶汽车的可靠性。实现智能汽车感知决策系统与车辆本身系统的一体化设计将在很大程度上缓解甚至消除这些问题。

无人驾驶智能汽车一体化设计是指综合考虑无人驾驶汽车对行驶环境的感知和决策以及车辆的动力学特性之间的相互联系和影响，将汽车动力学特性与环境感知决策进行有机的结合，在构建的无人驾驶汽车平台上集成设计各个模块及其相关过程。智能汽车一体化设计主要包含以下 4 个方面：

设计无人驾驶汽车集成平台，构建开放式模块化的多模态异构信息集成体系，并与汽车信息交互系统、仪表电器和电力控制系统协调控制。基于该集成平台，无人驾驶汽车能够实现无人驾驶和有人驾驶的无缝切换，做到在无人驾驶模式下，一旦人工因素介入，立即转换为有人驾驶模式，并且保证信息在体系结构中正常工作。

车辆发动机与变速器、制动系统的一体化纵向系统性能设计。车辆动力传动系统匹配得好坏直接影响汽车动力性、经济性、排放性、乘坐舒适性、驾驶安全性和操纵简易性等重要指标。动力传动一体化设计和电力控制制动系统的设计决定了车辆的纵向动力性和制动的安全等性能。

车辆转向系统有人驾驶与无人驾驶系统性能一体化设计。自动转向系统的设计决定了车辆的横向有关性能。现在汽车上基本都配备了 EPS，在进行无人驾驶汽车自动转向系统设计时，不能直接采用有人车辆的 EPS 控制器进行控制，需要根据无人驾驶车辆的特性要求，重新设计转向控制系统，实现其精确控制。

结合传统的汽车动力学，研究无人驾驶汽车动力学试验体系与方法。当有人驾驶汽车发展为无人驾驶汽车后，其操控性能也会发生变化。一方面无人驾驶汽车在行驶过程中不再需要考虑操纵系统人机工程学的约束；另一方面输入激励参数也发生了变化，这便要求对无人驾驶汽车重新进行参数测试和标定。

参考文献