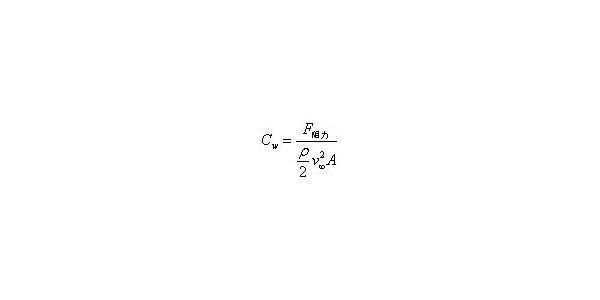
人们期望汽车可以在路面上行使可靠,其中一种路况是高速公路,当车辆在如图1所示的高速公路上行驶时,水进入发动机舱,有时到达进气管道和电气部件的位置并导致可靠性问题。在高速公路上行驶时的性能影响发动机舱的设计,数值模拟是该领域的一个有效工具,因为它不仅可以在实验前评估水位,而且可以识别浸水路线,了解进水现象并得出对策。

图1 车辆在水淹道路上行驶的情况
Yamamura等人开发了模拟方法,用CFD预测进气区域的水位,并用多元回归分析确定了确定水位的因素。这项研究假设车辆固定在一个固定的位置,而水的流速等于车辆的正常行驶速度。近来,为了提高空气动力学和外部噪声性能,发动机冷却模块周围的空隙趋于变小,并且底盖趋于比以前更大。在发动机舱周围的泄漏密封性变得更高,并且在高速公路上行驶时引起从水到车辆的浮力增加。因此,车辆的姿态改变正在对水位造成更大的影响。此外,要确定水位在预期水平内达到最高水平的情况则更加困难。本文介绍了建立模拟技术来预测发动机舱内的水位,考虑到由于水的压力引起的车辆运动。讨论了车速,水深和悬架模型变化的情况以及水上升机理。
仿真方法
数值方法论
在这项研究中,耦合多体和流体动力学方法被开发来预测车辆周围的水位。对车辆周围的水流进行了模拟,并通过流体动力学分析计算了从水到车辆的浮力。将其力传递给多体动力学分析,计算车辆姿态。此外,车辆的姿态反馈给流体动力学分析。换句话说,流体动力学分析和多体动力学分析是严格耦合的。
流体动力学分析方法
采用MPS(移动粒子半隐式)方法模拟自由表面流动。MPS方法是具有自由表面和无网格拉格朗日方法的不可压缩流体方法。在这种方法中,流体由粒子表示,流体的行为被计算为粒子的运动。因此这种方法不需要网格。这点非常有用,因为没有必要根据车辆姿态重新计算模拟网格,并有助于减少模拟时间。用质量连续性方程(1)和N-S方程(2)表示控制方程。
在粒子相互作用模型中,使用权函数(方程(3))来计算与其相邻粒子间的相互作用。
相互作用仅对有限距离内的粒子起作用,使用潜在模型来计算表面张力。上述控制方程的数值设定和特性设置如表1和表2所示,粒径是根据模拟结果的收敛性来确定的。
表一 MPS方法的数值设置
表二 水的参数设置
作为本研究的初步计算,该MPS方法被应用于图2(车辆模型)和图3(测试区域)简化车辆的水上行驶问题。四个车辆的初始速度和水深发生了变化。该计算的数值设置与表1不同,因为简化车辆的尺寸远小于整车。粒径设定为3mm,影响半径为6.3mm。图4显示了实际和模拟之间简化车辆前方最大水位的比较。水位被定义为离坡路的高度。从图4可以看出,仿真结果与实验结果吻合较好。准确度在±5%以内。通过这些计算,本研究证实了车辆路径运行的有效性。
图2 简化车辆模型
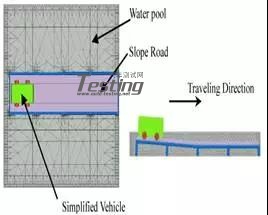
图3 测试区域

图4 实验和仿真对比
多体动力学分析方法
机械部件被模拟为刚体和质量属性分配给车身,每个刚体都受到固定,旋转和平移连接的限制。在这个机械系统上施加外力,并且在微分运动方程和代数约束方程的基础上计算物体的运动。在这项研究中,使用FunctionBay公司的RecurDyn V8R4进行多体动力学分析。
分析几何流体动力学模型
流体动力学分析模型由分析区域(图5)和车辆模型(图6)组成。分析区域以丰田的水下试验场道路为基础,坡度角,水路宽度和侧墙高度与实验室相同。车辆模型由10部分组成,车身,四个底部弹簧,轮胎和车轮以及后梁。这些零件的建模仅在外表面复制,与空气动力学分析相似的建模。(图7)模拟了热交换器周围的面部区域和屏蔽状态,其对发动机舱内的水位有很大的影响。零件相互独立,通过多体动力学分析的约束相互连接。将隔室内的换热器建模为体积区域,并将通水阻力定义为水流速度和压差的函数(图8)。
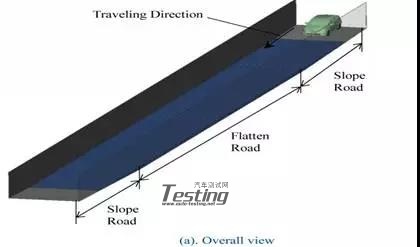
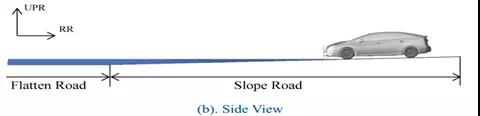
图5 分析区域
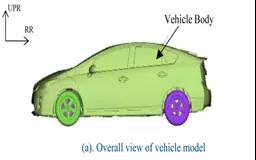
图6 汽车模型

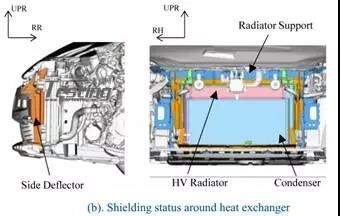
图7 车辆局部细节

图8 水的热交换特征图
多体动力学模型
使用图9所示的多体动力学模型。这个模型由流体动力学分析的10个部分和车辆模型组成。所有部分都被认为是刚体,每个刚体的质量和惯性矩都被确定下来,所有部分都相互制约。对于前悬架,两个下弹簧通过旋转接头与每个轮胎和车轮连接,并且这两个下弹簧通过平移接头与车身连接。对于后悬挂,两个下弹簧通过旋转接头与每个轮胎和车轮连接,并且这两个下弹簧与后横梁固定,后横梁通过平移连接与车身连接。弹簧和阻尼系数定义为四个平移关节。为了减少数值波动,在轮胎和地面之间施加气缸到地面的接触条件。滚动阻力系数被施加到轮胎表面以计算滚动阻力。
图9 多体动力模型
模拟条件
仿真案例
表3显示了仿真案例,模拟了十一个案例。在这些情况下,改变车速,水深和悬架模型,以验证所开发的方法,根据车辆状况比较水位,明确使用耦合多体和流体动力学分析的必要性。比较两种悬架模型,活动模型和刚性模型。本研究采用柔性模型来重现车辆的姿态,刚性模型使车辆姿态在静止状态下固定。换句话说,即使来自水的浮力作用在车辆上,车辆也不能在垂直方向上移动。

表三 模拟方案
运行条件
基于图10中的实验数据定义车辆速度。时间是由通过测试车辆从入口坡顶到达路面终点时的时间来标准化,以便容易地比较不同的车辆速度状况结果。车速取决于驱动力与水阻力之间的关系,当阻力小时,车辆可以以目标速度行驶(情况1和5)。然而,当阻力高时,车辆不能保持在水中的目标速度,可以以较低的速度行驶(情况4和6)。
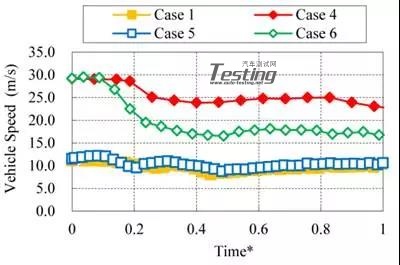
图10 1、4、5、6方案下车速
结果
验证
通过实验结果与模拟结果的比较验证了所开发方法的有效性。图11显示了最大水位的比较结果。水位定义为每个传感器下端的高度。图12显示了水位传感器的位置,这些位于发动机冷却模块(ECM)的前部和后部,精确度在简化的车辆情况下的±5%以内(图11)。水位时程曲线比较如图13所示。比较结果显示,不仅水位高度一致,而且悬浮位移也很好。将车辆周围的流场与实验进行比较(图14)。从定性和定量两方面来看,模拟可以准确地再现实验中观察到的自由表面的形状。
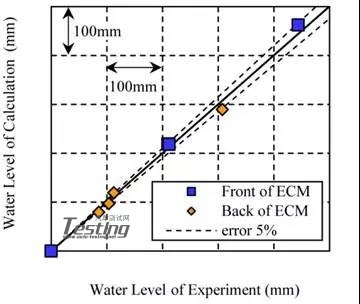
图11 1、4、5、6方案下水位变化
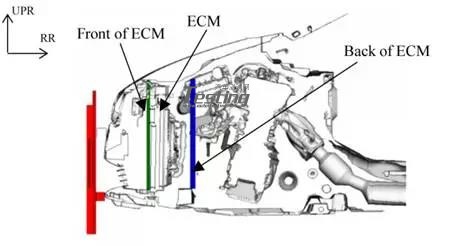

图12 水位传感器的位置
图13 试验和仿真结果的比较(方案6)

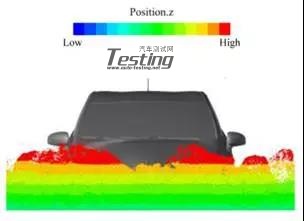
图14 汽车周围流场的比较(方案6,时间*=0.8)
水深200mm水位结果
发动机舱内水涨的现象根据车速分为2种模式。图15显示了每种情况下发动机冷却模块前后水位的时间历程。在这种情况下,车辆进入路面的时间大约是时间*=0.15。在案例1和案例2中,ECM前面的水位在进入后不久就上升,达到最高水平,之后下降并转换到几乎恒定的水平。后面的变化和前面的变化几乎一样,但是水平是一样的比前面小。另一方面,在Case3和Case4中,水平并没有上涨一段时间,从ECM的后面上涨。
图16显示了Case1中Time*=0.25和Time*=0.8时的流场。在这种情况下,水从前格栅进入发动机舱并转换到稳定状态。因此前侧的水平高于后侧的水平。Case1和Case2所代表的这种变化被定义为模式I。
图17显示了Case4中Time*=0.3和Time*=0.6时的流场。图18显示了Case1和Case4之间的前悬架位移的比较。在这种情况下,水从发动机罩下方的间隙进入发动机室,并从ECM的后面移动到前面。悬架位移比Case1大得多(图18)。因此前侧的水位低于后侧的水位。改变以Case3和Case4为代表的模式被定义为模式II。基本上,所有案例的结果都表明,模式一的水位高于模式二。

图17 方案4流场
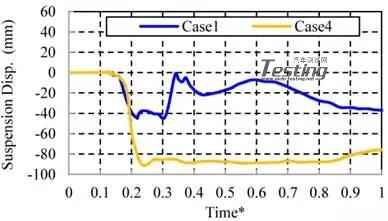
图18 前悬架位移比较
水深300mm水位结果
根据水深200mm的结果分类,总结了水深300mm的结果。图19显示了每种情况下的水位时间历程。在这种情况下,进水时间为时间*=0.15,水深为200mm的情况。在案例5中,与案例1和案例2类似,水位在入场后不久达到最大值。因此,Case5被分为模式I.在案例6中,水位没有上升一段时间,从ECM的后面上升,类似于模式II(Case3和Case4)。然而,水平从时间*0.5左右开始上升,特别是前面比后面有上升的趋势。图20显示了Case6中Time*=0.3,Time*=0.5,Time*=0.7时的流场。
起初,进入发动机舱的水主要来自发动机罩下的空隙(时间*=0.3),即模式是模式II。之后,水从前格栅进入并且前侧的水位超过了后侧的水位。即,模式转换到模式II。
综上所述,在案例6中,模式II的流场形成于第一和第二,然后改变为模式I的模式。
图19 300mm水深的水位线
图20 方案6的流场
车辆姿态对发动机舱的影响
水位
最大水位比较悬架模型,灵活和刚性模型。图21显示了每种情况下最大水位的比较。对于所有刚性模型的情况,无论传感器位置如何其值均超过了柔性模型的单调性,均取决于车辆速度而增加。另一方面,对于灵活的车型,这些值根据车速而复杂地增加或减少。
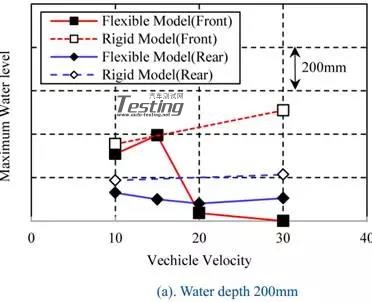
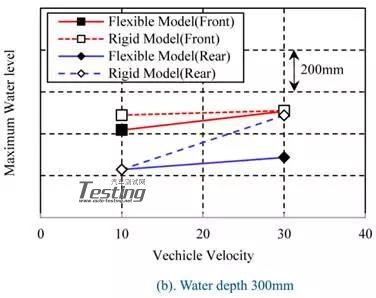
图21 两个悬架模型的比较
讨论
结果表明,所有病例按进水路径分为2类,Ⅰ类水位高于Ⅱ类水位。在这一节中,模式I和模式II之间的机制差异被阐明,并且运行条件被分类。
模式I和II之间的机制差异
为了揭示水上涨机制,考虑了水面典型流线和能量的变化。在水粒子与车辆接触之前,假设由动能和势能组成的总能量应该被保留(方程(4))。
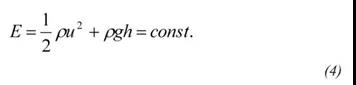
其中E表示总能量,ρ是密度,u是水粒子与车辆之间的相对速度,g是重力加速度,h是水位从车辆的角度来看,水面颗粒运动的示意图如图22所示。
图22 水粒子位置与能量的关系
据推断,在模式I中,粒子的动能转换为势能,另一方面在模式II中动能不转换并保持为动能。而且,假设模式I和模式II之间的差异是下保险杠前缘(hb)的高度和水面的高度之间的相对位置。为了验证上述模式I的推导,比较Case5和Case10的流量,如图23所示。在这些情况下,设定相同的车速和相同的水深,但悬架模型不同。在这两种情况下,车辆前方地面的水位几乎相同(图23)。因此,即使车辆姿态不同,车辆前方的水位在相同的测试条件下也保持不变,但发动机舱内的水位在很大程度上受车辆位置的影响。Case3(速度幅度分布)的流场如图24所示。图24的速度是从车辆的角度来看的相对值。在这种模式中,在颗粒碰撞车辆之前,速度保持恒定。因此,车辆前方的水位实际上是相同的,而不涉及车辆姿态。但是,发动机舱内的水平根据车辆姿态而变化非常多。因此,为了更精确地预测发动机舱内的水平,推测考虑姿态是重要的。
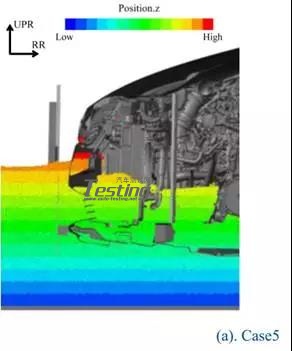
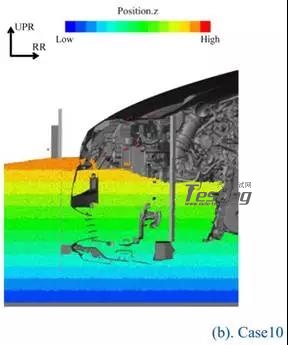
图23 方案10和方案5流场比较
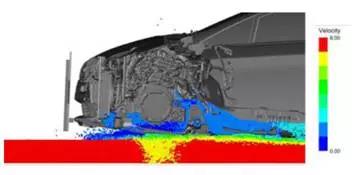
图24 速度大小分布(方案3)
运行条件的分类
图25中示出了在路面上行驶时作用在车辆上的力。在车身上,重力,来自水的浮力和来自弹簧的反作用力在垂直方向上平衡,并且来自水的阻力来自驱动轴的驱动力在水平方向上平衡。
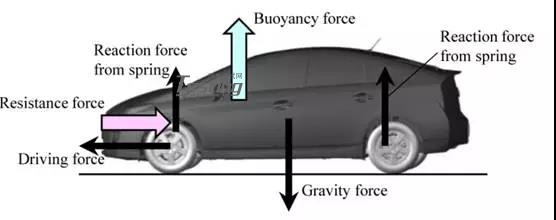

图25 涉水道路上行驶车身上的作用力
考虑到上升机构的形式是由车体的垂直位置决定的,推测可以从以下方式对运行状况进行分类。
i. 垂直位置由垂直力平衡决定,因此受到浮力的影响。
ii. 浮力由车速决定。
iii. 车速由水平力平衡决定,因此受到水的阻力影响。
图26显示了阻力和车速之间的关系。基本上,对于每个水深,阻力随车速的平方增加。
图26中的黑线表示驱动力的限制。车辆不能越过黑线。实际上,Case6的阻力大于动力,车速从30km/h降到17km/h。图27显示了车速和浮力之间的关系。而图28显示了浮力与下保险杠前缘(hb)离地面的高度之间的关系。
通过以上讨论(模式I和模式II之间的机制差异),推测机构模式由下保险杠前缘高度与水面高度之间的相对位置决定。例如,在水深200mm时,如果下保险杠前缘的高度低于200mm,则壳体被分类为图案I。另一方面,当高度大于200mm时,表壳被分类为图案II。事实上,案例1和案例2分为模式一和案例三,案例四分为模式二。
基于上述考虑,可以得出结论:可以确定模式I和模式II之间的界限。与图26,27和28结合的图形如图29所示。从左下象限,图案I和图案II之间边界的浮力由边界高度决定。从右下象限,边界的车速由浮力决定。最后,从右上象限,阻力由车速决定。图29中的红线表示模式I和模式II的分隔线。从图29可以看出,运行条件可以分为两种机制模式,红线是模式I和模式II的边界。
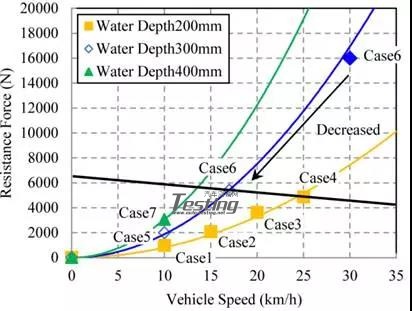
图26 车速与阻力的关系
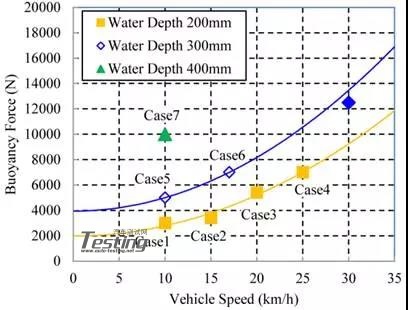
图27 车速与浮力之间的关系
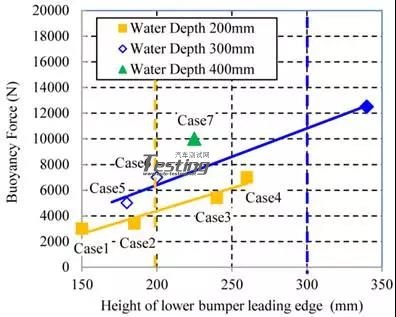
图28 下保险杠前缘高度与浮力之间的关系
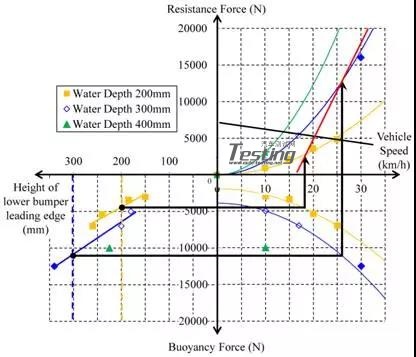
图29 两种模式数的上升机理分类
结论
通过耦合多体和流体动力学,开发了用于预测发动机舱内水位的模拟技术。预测方法精度在±5%以内,水位和悬浮位移时程与实验吻合较好。通过对车速,水深和悬架模型改变的几种情况的仿真结果,得到以下结论。发动机舱内水涨的现象根据车速和水深分为2种模式。在模式I中,水主要从前格栅进入发动机舱,并且在模式II中从发动机盖下的间隙进入发动机舱。基本上,模式I的水位高于模式II的水位。可以得出结论,车辆前方的水位由运行条件决定,但发动机舱内的水位因车辆姿态而异。通过考虑在高速公路上行驶时的车辆作用力,可以将运行条件分为2种模式。

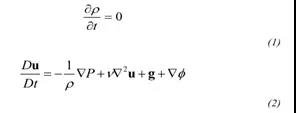
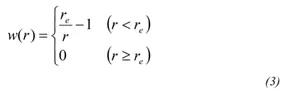

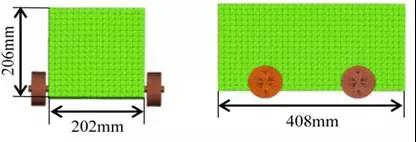


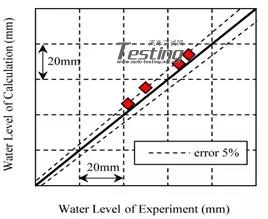

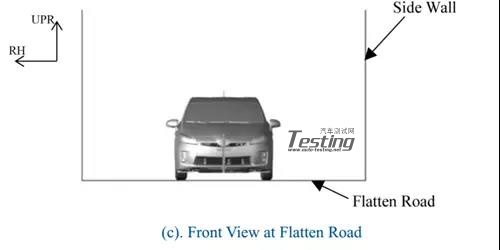



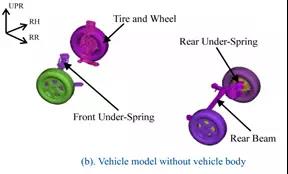



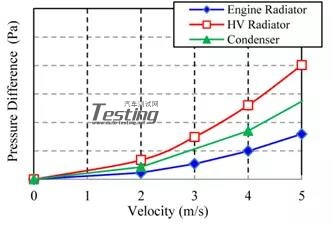
 图8 水的热交换特征图
图8 水的热交换特征图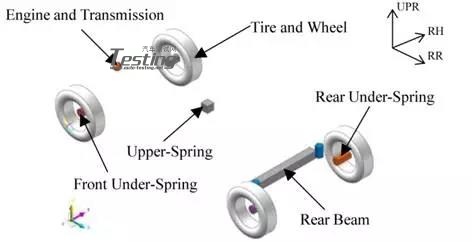







 图12 水位传感器的位置
图12 水位传感器的位置


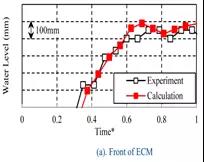
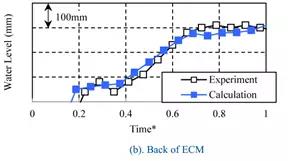
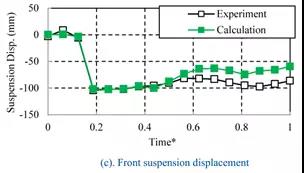





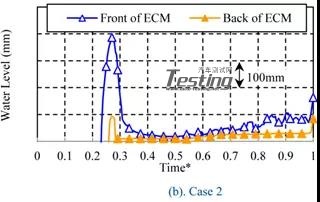
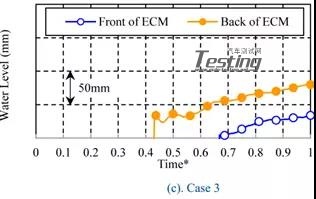
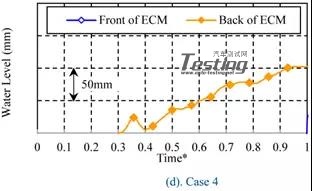


 图15 200mm水深的随随时间的水位
图15 200mm水深的随随时间的水位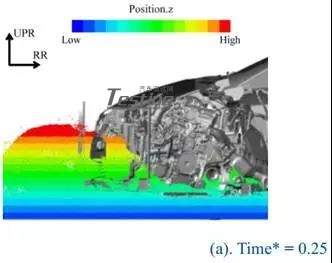
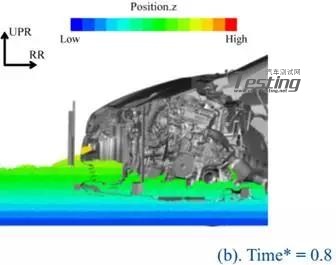
 图16 方案1的流场
图16 方案1的流场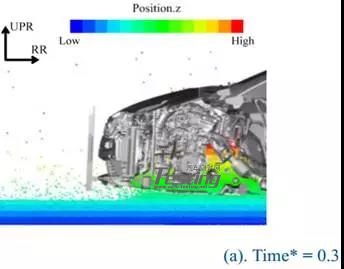
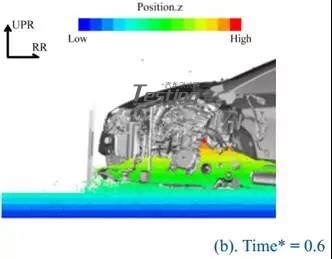
 图17 方案4流场
图17 方案4流场



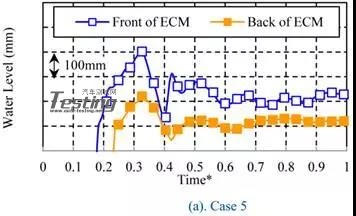
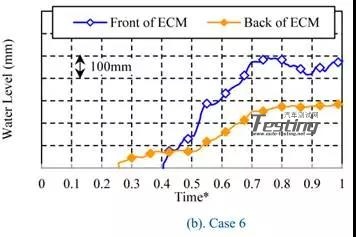

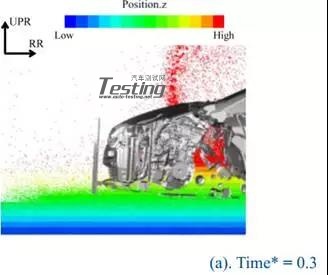
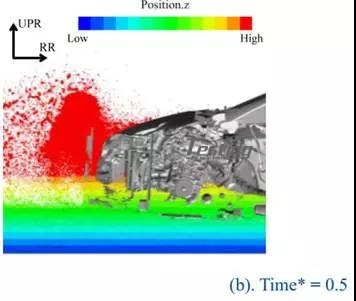
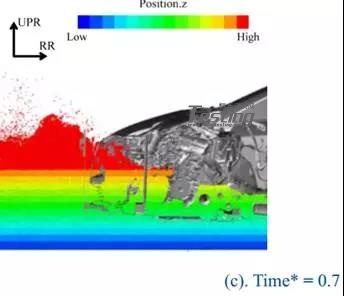






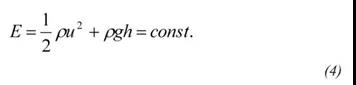



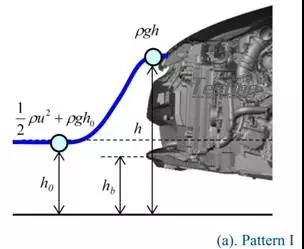
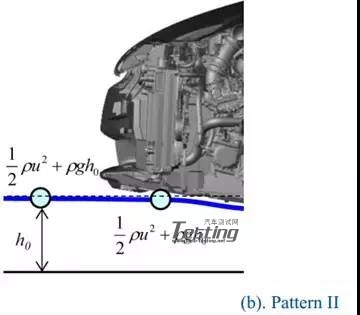







 图25 涉水道路上行驶车身上的作用力
图25 涉水道路上行驶车身上的作用力












 广告
广告