汽车结构件疲劳耐久分析（二）：金属疲劳理论之一

1.金属疲劳理论简史
现代的金属疲劳理论起源与第一次工业革命时期，在两百年当中逐步发展，现如今已经是一门在工程界广泛应用的学科，但同时，金属疲劳也还有许多尚未解决的问题。

• 1839年，Poncelet 首先使用“疲劳”一词。
• 1849 年，英国机械工程学会（IMechE）辩论结晶理论。
• 1864 年，Fairbairn 用交变载荷对船链进行了实验。
• 1871 年，Wohler首先对铁路车轴进行了系统的疲劳研究。发展了旋转弯曲疲劳试验，S-N曲线及疲劳极限概念。
• 1886 年，Bauschinger 首先确证了应力-应变滞回线。
• 1903 年，Ewing 和Humphrey 证明结晶理论是不正确的，指出疲劳是由于塑性变形所引起。
• 1910 年，Bairstow 调查了应变循环中的应力-应变响应，提出了循环硬化和循环软化概念。
• 1920 年，Griffith 研究了玻璃中的裂纹，由此诞生了断裂力学。
• 1955年，Manson 和Coffin 研究了应变条件控制下的疲劳，热循环、低周疲劳及塑性应变问题。
• 1959 年，Paris 首先提出了一种用断裂力学参数处理裂纹扩展的方法。
• 1961 年，Neuber建议了一种方法，估计应力集中处的弹塑性应力应变。
• 1968 年，Matsuishi 和Endo 提出了雨流循环计数方法。

疲劳耐久是一门非常古老的技术方法，现在教科书上讲到的S-N方法和疲劳极限就是Wohler在1871年通过对火车车轴进行研究后发展出来的疲劳耐久分析方法，时至今日仍然具有广泛的应用。在工程应用中，疲劳耐久的计算由许多经验公式组成。这些经验公式根据一些理论框架，从材料、零件或结构的疲劳试验数据中拟合而成，它们往往能够解决一些相对应的疲劳问题。

2.金属疲劳失效的机理
疲劳是零件由于循环载荷引起的局部损伤的过程。材料在反复加载的作用下，即使把应力幅度严格控制在材料的弹性范围以内，也总会发生断裂，即会发生疲劳损坏。这是一个由包括零件裂纹萌生、扩展和最终断裂等组成的累积过程所导致产生的综合结果。产生疲劳失效的外因是零件受到了变化的载荷，而内因是金属中天然存在的位错、滑移带或夹杂物、疏松等能够引起高应力集中的缺陷。





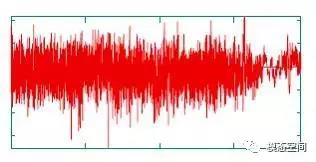
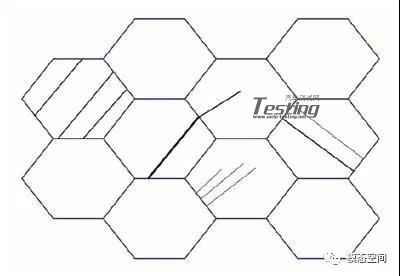
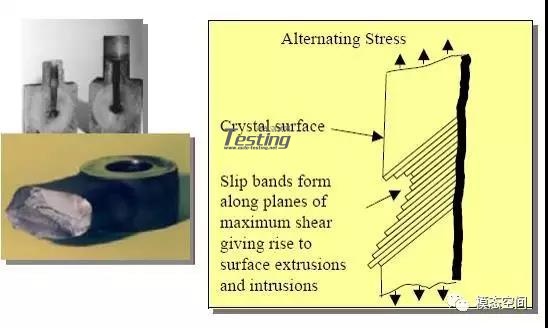
在循环加载期间，在最高应力区域发生局部塑性变形。这种塑性变形引起零件的永久损伤和裂纹扩展。随着零件所承受的加载循环次数不断增加，裂纹长度（损伤）随之增加。在达到一定循环次数之后，裂纹将导致零件失效（断裂）。

通常，疲劳过程可以观察到以下几个阶段：1，裂纹成核；2，微观裂纹扩展；3，宏观裂纹扩展；4，最终断裂。裂纹在接近高应力集中的局部剪切面上启裂，如稳定滑移带、夹杂物、疏松或晶粒不连续分布等。局部剪切面通常发生在晶粒表面或边界之内。在这一阶段，裂纹成核是疲劳过程的第一步。一旦裂纹成核并且持续施加循环载荷，裂纹就会沿着最大切应力面和晶粒边界扩展。



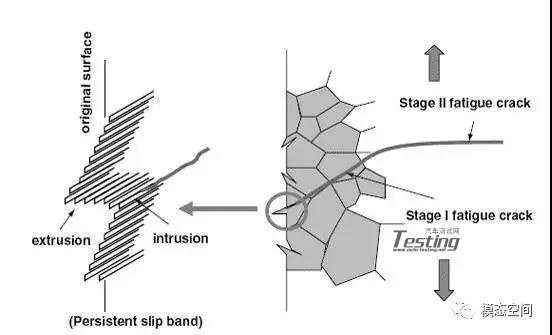
从上图中可以看出，裂纹成核始于稳定滑移带中最高应力集中区域。第二步是裂纹扩展阶段，分为裂纹第一和第二扩展阶段。通常认为，在第一阶段，认为裂纹成核和扩展是初始微观裂纹在局部最大剪应力面上沿着大约几个晶粒的有限长度扩展。在此阶段，裂纹尖端塑性受到尖端特性、晶粒大小、方位和应力水平的极大影响，因为裂纹的大小是与材料的显微结构等量齐观的。第二阶段裂纹扩展是指宏观裂纹扩展，通常主要在主拉应力面法向扩展，部分沿着最大剪切力方向扩展。与第一阶段裂纹相比，这一阶段的宏观裂纹特性受显微结构特性的影响要小。这是因为第二阶段裂纹的裂纹尖端塑性区域要远大于材料的显微结构。

在工程应用中，通常将零件在裂纹成核和微观裂纹扩展期间的寿命长度成为裂纹萌生阶段，而将零件在宏观裂纹扩展期间的寿命长度称为裂纹扩展阶段。通常，对从萌生到扩展的过渡阶段无法做出精确的定义。但对于钢材而言，在萌生阶段结束时的裂纹尺寸大约为钢材的几个晶粒大小。此裂纹尺寸的范围一般为0.1mm~1.0mm。钢制零件的裂纹萌生阶段一般占其疲劳寿命的大部分，特别是在高周疲劳状态下（大约>10000次循环）。在低周疲劳状态下（大约<10000次循环），疲劳寿命的大部分时间耗费在裂纹扩展。由于断裂一般是突然发生的，疲劳寿命主要由裂纹形成和裂纹扩展两个阶段构成。与这两个阶段相应的寿命分别称为裂纹形成寿命和裂纹扩展寿命，它们共同构成疲劳全寿命。



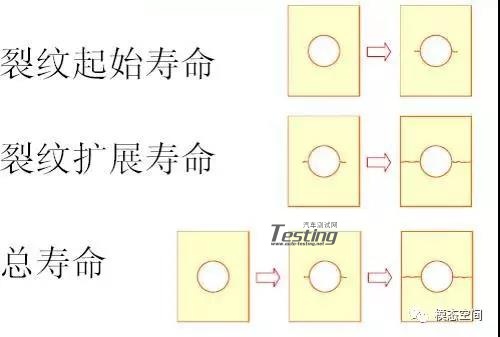
在许多汽车零件中，有用寿命的大部分都消耗在形成1～2mm长的宏观裂纹上。比如具有轻度应力集中（理论应力集中系数Kt < 4）、由韧性金属制成、并且受到具有零或拉伸平均值的载荷历程作用的零件，就属于这种情况。

3.名义应力法（S-N）
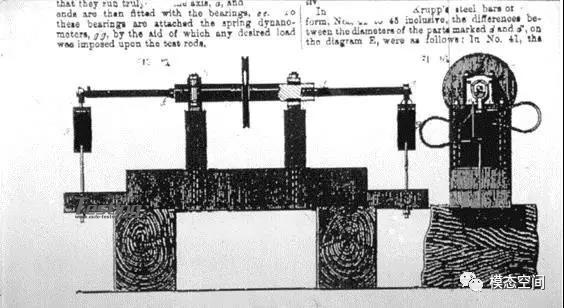
从19世纪中叶以来，疲劳分析和设计的标准方法都是以应力为基础的。在1852年-1870年间，德国铁路工程师奥格斯特·维勒（August Wohler）首次进行了系统性的疲劳研究。



现在这种恒幅应力循环疲劳试验被称为经典维勒试验。这种方法也被称为名义应力法或S-N法。S-N法有以下几个特点：

• 循环应力是疲劳失效的控制参数；
• 高周疲劳条件表现为：疲劳失效循环次数高；
• 循环加载塑性变形小。



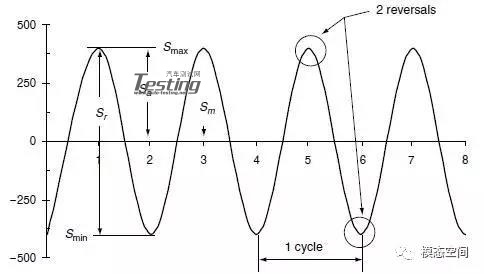
疲劳试验期间，试样承受交变载荷的作用，直至发生疲劳失效。在试样上所施加的载荷，由恒定应力范围或恒定应力幅确定。应力范围被定义为一个循环中的最大应力和最小应力之间的代数差，应力幅等于应力范围的一半。通常，疲劳分析的法则是拉应力为正，压应力为负。应力范围或振幅的量值为可控变量，而至疲劳失效的循环次数为响应变量。至疲劳失效的循环次数为疲劳寿命，且每个循环有两次反向。通常，采用对称循环的交变加载方式进行S-N疲劳试验。



在特定的疲劳寿命区间，采用不同的对称循环应力幅分别对几个相同试样进行应力-寿命试验。将疲劳试验的数据绘制在对数坐标上，如下图所示。这条曲线被称为S-N曲线或者维勒（Wohler）曲线。负斜率的曲线或者直线部分被称为有限寿命区域，水平线被称作无限寿命区域。在S-N曲线上，负斜率线与水平线的交点称作S-N曲线的拐点，表示疲劳极限或者耐久极限。



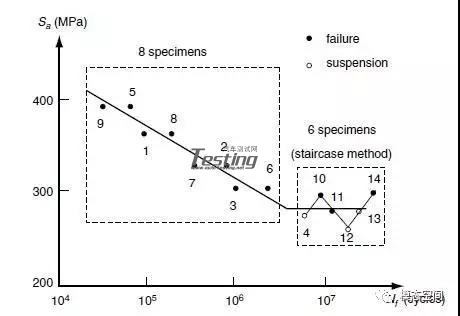
下面这个方程表示典型的S-N曲线：



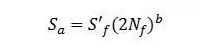
在采用应力方法开展疲劳分析和设计时，这个由双对数S-N曲线图得到的表达式是应用最广泛的方程，被称为巴斯坎方程。式中b为疲劳强度指数；S‘f为疲劳强度系数。要注意到，这里的应力Sa指的是循环名义应力，名义应力的确定取决于加载方式和试样结构。S-N法基于这样一个假设，具有同样名义应力的试件具有相同的寿命，它的主要局限性是没有考虑缺口根部的塑性，而这种塑性正是疲劳的原因。不能预测局部塑性和平均应力的影响。