自动驾驶汽车的运动规划技术综述

运动规划
90年代以前,由于投资的减少,智能车辆领域发展十分有限。得益于适用于车辆自动化信息技术的发展,形成了智能交通系统的概念。世界范围内诸多研究中心(比如加利福尼亚的Path团队,帕尔马大学等等)的投入,为智能车辆系统的提升注入了源源不断的力量。第一辆自动驾驶概念车的历史可追溯到80年代末期90年代初。当时,为了提升公路系统的服务能力,Shladover等人提出了一种车辆的纵向控制系统(包括车辆的跟随控制,车间通信,及与其他技术的比较)和横向控制系统(考虑横向动力学和磁力传感器作为路径引导物,并未涉及路径规划)。而Behringer等人则提出VaMoR-L车辆中集成的自动驾驶概念——通过视觉和路径生成,车辆可以自动驾驶(来源自其普罗米修斯项目)。
随后,自动驾驶衍生出许多控制架构。如图1所示,感知,决策和控制是主要的三大块。本文主要介绍决策当中的运动规划技术。
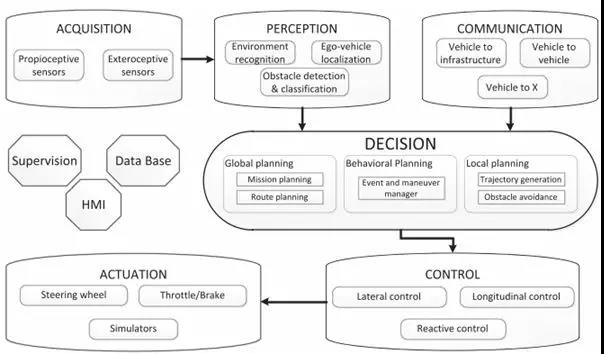
图1 自动驾驶控制架构
在近几十年,运动规划开始作为移动机器人的一个研究分支。研究学者也将运动规划划分为全局规划和局部规划。大量的路径规划技术从移动机器人当中迁移到自动驾驶车辆领域,并根据所面临的道路网络与驾驶规则要求得以改进。这些规划技术按照实现方法,大致可以分为四大类——图搜索,采样法,插值法和数值优化。
图搜索
对自动驾驶而言,其基本思想是从A点到B点遍历一个状态空间。这个状态空间多用占有栅格或晶格表示。自动驾驶当中实现的方法有:
Dijkstra算法
这是在图表中找到单源最短路径的图搜索方法。搜索空间近似为一个离散的单元格,晶格[22,23]。具体描述和实现可见文献[24,25]。在自动驾驶方面,文献[26]实现了该算法在多车场景的仿真,Little Ben 自动驾驶车[27] 和Victor Tango团队 [28] 上都有该算法实现。文献[29]实现了该算法在城市工况下的应用。
A*算法
其核心是节点权重该如何确定。它适合具有先验知识的车辆进行空间搜索,但又太消耗存储和计算速度[30]。在移动机器人领域的一些应用被自动驾驶采用,并作为基础进行改进。例如dynamicA* (D*) [31],Field D* [32],Theta* [33],Anytimerepairing A* (ARA*) 以及 Anytime D*(AD*) [34]等等。Ziegler等人在Voronoi地图表征的非结构化空间和泊车点实现了A*算法[35]。文献[36]和文献[37]分别是hybrid A*和A*在Junior和AnnieWay自动驾驶车辆上的应用。BOSS自动驾驶车使用的是AD*算法[16]。
状态晶格算法
采用由状态网格组成离散的规划空间。这些网格被称为状态晶格,并在基于此进行搜索规划[46]。路径搜索是基于局部一系列的状态晶格查询或是包含所有可行特征的查询,它允许车辆从一个初始状态转移到其他状态。代价函数确定了状态晶格地图的最佳路径。A*[47]和D*[48]在该方法中都有实现。Howard和Kelly将状态晶格应用到了轮式移动机器人在崎岖路面的运动规划当中[49],仿真表明该方法具有全局和局部比较好的结果。文献[39]和文献[50]采用了时间维度和速度维度的状态晶格。
采样法
这一类方法是为了解决时间的约束(在高维空间规划)。这一过程包含在特征空间或状态空间的随机采样,并寻找采样点在这个空间里面的连接[21]。缺点在于结果的次优性。在无人车当中使用最为广泛的是快速随机扩展树(RRT)[94]。
RRT适用于在线的路径规划,通过在导航区域执行随机搜索,可以在半结构化空间实现快速搜索[94]。它还可以考虑非完整性约束。文献[21]和文献[95]对该方法进行了阐述。在自动驾驶方面,MIT团队实现了该算法[61],但是结果并不是最优,而且路径曲率不连续。Karaman等人提出了一种RRT*[96]的改进方法,它可以得到最优路径,但存在其他同样的弊端。文献[64]也对其有描述。
插值法
对于给定一系列路点,计算机辅助几何技术(CAGD)在路径平滑方面有很广泛的应用[73]。它可以考虑诸如可执行、舒适性、车辆动力学以及其他参数的约束来规划轨迹。
插值是在预先给定一系列点的情况下构造和插入一系列新的数据点的过程。这表明算法需要预先给定一系列节点,然后生成一系列有助于轨迹连续、满足车辆约束和动态环境的导航轨迹[97]。在面对障碍物时,它能够产生避障的新路径(局部路径),并重新回到先前规划的路径(全局路径)。
直线段和圆弧法
已知路网可以进行分段,在已知路径点插入直线或圆弧节点,使整段路径用直线段和圆弧代替。在轮式车辆的路径规划方面,这是一种简单的数学方法[41,98]。
回旋曲线法
这一类曲线是定义在Fresnel坐标下(菲涅耳积分)[73]。由于该方法的曲率对应于弧长变化,所以回旋曲线可以定义轨迹按曲率线性变化;可以实现直线段和曲线段在曲率上平滑过渡[42]。回旋曲线在高速、轨交和类车机器人的运动规划中同样使用,能够实现[99]。VIAC项目对回旋曲线的实现进行了测试。文献[69]中,当前曲率从转向轮的位置上获取,其他参数则考虑根据动力学约束(比如摆尾)或者物理约束(比如转向轮转角)获得。
多项式曲线法
这一类曲线通常用来满足插入点的所需求的约束,在位置拟合、转角和曲率约束等方面比较适用。起点和终点的期望值以及约束决定了曲线的系数。为了计算多项式曲线的系数,可以参考文献[76,77,79]。
研究车辆-基础设施-驾驶员之间交互的实验室(LIVIC)在换道场景中实现了这类算法[77]。四次多项式曲线用以满足纵向的约束,五次多项式曲线用以满足侧向的约束。文献[75]使用三次多项式曲线生成超车所需的安全轨迹。文献[43]在状态晶格中实现三次多项式曲线和四次多项式曲线的规划。
贝塞尔曲线
这种参数化曲线的形状由控制点决定。贝赛尔曲线的核心是伯恩斯坦多项式。由于曲线受控制点决定,这一方法的优点是计算量小。通过正确的放置控制点,起始点和终点的曲线约束可以得到满足[81,100]。
文献[100]展示了贝赛尔曲线的一个很好的模块化和可扩展的例子,文献[102]设计了一个满足曲率连续的圆形和贝赛尔曲线相连接曲线轨迹。这些曲线常用以近似回旋曲线[103,104],或者是快速规划时替代严格的贝塞尔曲线[85,86]。文献[81,83,44]在自动驾驶上实现了三阶和四阶贝赛尔曲线,并评估了不同场景(转向、迂回、换道、避障等等)的最佳操作曲线。
样条曲线
是分段多项式参数曲线,分段曲线可以是多项式曲线[28,76],B样条曲线[88,89],贝赛尔曲线[105]或者是回旋曲线[99]。分段曲线的连接点叫节点,它一般具有高度平滑性的约束。一个B样条带变节点的例子如文献[45]所示。
数值优化
这一方法的目的在对带约束的目标函数进行最优求解,多用于计算平滑计算前的轨迹[54]或是计算满足运动学约束的轨迹[5]。函数最优化是为了找到目标函数的实根(最小化输出)。文献[106]利用改进势场法实现了在移动机器人狭窄空间避障的C1连续曲线规划。文献[5,38]也利用最小化考虑了位置、速度、加速度、加加速度的目标函数寻找C2连续曲线。
图2展示以上所提运动规划技术的效果,表格1和2对运动规划技术以及优劣进行整理。
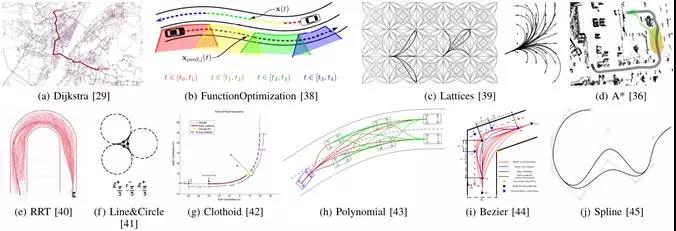
图2 文献中的运动规划方法
表1 自动驾驶不同场景下应用的运动规划技术分类
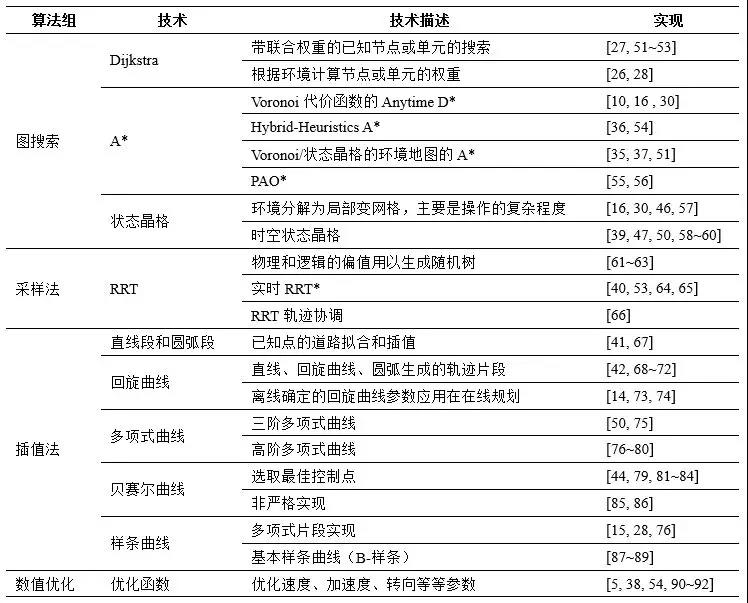
表2 运动规划技术的优劣对比

世界范围内,智能交通系统研究团队所推动的运动规划技术
智能汽车的概念虽然可追溯到1939年纽约世博会,但是,其实现却花费了数十年。图3以时间轴的形式展示了自动驾驶汽车的重要发展节点。
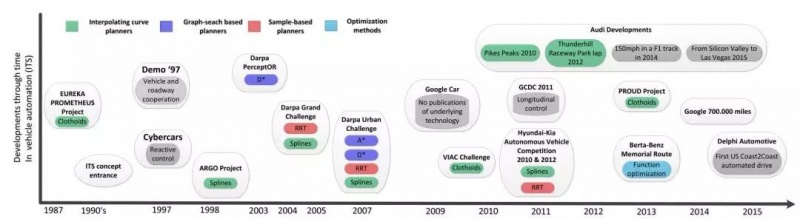
图3 重要无人驾驶车辆及其运动规划技术随时间的发展
自1987年到1994年间,欧洲的尤里卡普罗米修斯项目是智能车研究的先锋,这其中,来自戴姆勒和沃尔沃等工业合作伙伴的不同汽车都是自动驾驶。弯曲部分路径用螺旋线实现以辅助控制系统实现循迹[14]。
在与通用汽车的合作下,PATH项目在加州圣地亚哥展示了其作为Demo’97部分内容的队列驾驶。队列由8辆行驶在专用车道上的汽车组成,车间间距6米。卡内基梅隆大学也参与其中,并演示了Navlab 车辆[113]。同年,一份来自荷兰的报告介绍了首次应用于史基浦机场的CTS服务[114],所解决的是最后一英里问题——提供上门服务以及按需服务[115]。在上述系统中,环境反应控制和车路协同要优于路径规划技术进行考虑。
首次尝试路径规划技术的项目中,VisLab的ARGO算是其中一个[76]。基于视觉系统,规划将五次多项式样条曲线调整到前视相机检测标定到的车道当中。之后,DARPA PerceptOR项目进行了越野车的自动导航仿真[116][117],它是由DARPA挑战赛(Grand and Urban challenge)所完成的,这促进了自动化导航系统的研究,推动了路径规划技术发展(如图2所示)。
自2009年谷歌车辆进入市场,谷歌在诸多场合展示其自动驾驶能力,获得超过了700000英里无事故的行驶里程。谷歌也在推动这项技术的立法,并于2012年5月获得自动驾驶车辆的首个许可(两个月后,内达华州颁布了首个自动驾驶汽车的法令)[118]。然而,并没有谷歌自动驾驶中运动规划和控制方面的技术公布。
2010年举行的视觉实验室国际自动驾驶挑战赛(VISC),车辆以自动模式从意大利(帕尔马)到中国(上海)行驶13000公里,规划当中主要考虑的是螺旋线生成的代价函数。同年及2012年,现代汽车在韩国本土举办了自动驾驶汽车挑战赛。2010年的挑战赛任务集中在循迹和避障。2012年的挑战赛任务集中在城市驾驶场景的理解与信号灯的检测[17]。涉及的运动规划技术包括螺旋线[18],[119],RRT[120]及其他技术。
2011年,欧洲举办的协同驾驶挑战赛(GCDC)以纵向控制开发为主[143]。然而,一些团队也开发了路径规划策略(例如AnnieWAY的状态格子[131])。接下来的2016GCDC挑战赛,队列的横向控制,拥挤道路条件下的并道和城市道路环境也将考虑进去。
最近,奥迪联合斯坦福[42][144]开发了高性能的车辆控制,实现了螺旋曲线的规划。参与的演示包括:2010年的派克峰攀登,2012年的雷山赛马场的一圈跑圈,2014年F1赛车速达150迈,2015年从硅谷到拉斯维加斯真实场景下自动驾驶。也就是在2015年,德尔福自动驾驶首次实现了从美国东海岸到西海岸,长达9天,从旧金山到纽约。表3列举了国际研究团队的情况。
表3 国际智能交通系统研究团队

总结
智能规划算法的开发是机器人研究领域的一大关键技术[20][21]。延伸到自动驾驶汽车,相关的约束包括交通规则,车速,道路条件,以及时间限制(复杂条件下规划到指定区域)等。本文从以下两方面对自动驾驶车辆运动规划技术进行了综述:一,对比分析了四大类运动规划技术(如表1所列),包括图搜索、采样法、插值法和数值优化的方法;二,调研了世界范围内主要智能交通系统研究单位所实现的运动规划算法(如表3所列)。
近年来为研究团队实车实现的两大主要算法分别是:
1、插值法。近年来,自动驾驶车辆所采用的规划算法有螺旋线(奥迪、帕尔马/VisLab,斯坦福),贝塞尔曲线(INRIA)和多项式曲线(戴姆勒,INRIA)。这是基于结构化道路环境下对地图信息的丰富——可以提供所需的加州道路交通路点的数据。此外,出于舒适性、安全性、车辆几何与动力学约束考虑,轨迹生成还需经过曲线优化这一步。
2、图搜索。状态格子是应用最广泛的方法之一,例如CMU、KIT、GMC等研究单位都有实现。在考虑到舒适性、安全性、车辆几何与动力学约束时,该算法可以快速搜索到最优路径,尽管该算法只具备解析完备性。
未来研究重点
运动规划现在所面临的挑战是动态环境下的实时规划问题。城市道路场景下,存在众多的交通参与者(比如,行人,骑自行车的人,其他车辆等),这要求对所规划出来的轨迹进行不断的评估。如何在有限的时间内实现多动态障碍无环境下的无碰撞轨迹生成是一个尚未解决的难题。难点主要在于耗时的环境感知[145]大大降低了运动规划的决策时间窗。目前所实现的算法还不足以克服这个限制。
由于规划是感知和控制之间的纽带,当前的新规划算法开发多考虑感知的不确定性以及控制的约束。在动态环境数据采集过程中,路径规划的最新发展目标是正确处理数据采集过程中的不确定性。这在实时的情况下会有更好的环境感知效果,并指导规划过程。通过考虑感知阶段的不确定性来提高防止危险情况的能力。从控制的角度来看,需考虑多目标,包括车辆的运动学约束和乘客的舒适性等。近年来,研究通过轨迹的平滑和可执行性来考虑这些控制约束。接下来的研究将可能是考虑控制约束的同时,融合感知的不确定性。KIT和CMU在这一方面已开始研究。
另一个趋势是增加驾驶员的大控制环,类似于ADAS的功能,通过HMI实现轨迹与驾驶员的交互。在确保轨迹安全、平滑与可执行的条件下,感知不确定性,控制约束,驾驶员知识的多融合将是一个新的极具挑战性的研究。
编辑推荐
最新资讯
-
中汽中心工程院能量流测试设备上线全新专家
2025-04-03 08:46
-
上新|AutoHawk Extreme 横空出世-新一代实
2025-04-03 08:42
-
「智能座椅」东风日产N7为何敢称“百万级大
2025-04-03 08:31
-
基于加速度计补偿的俯仰角和路面坡度角估计
2025-04-03 08:30
-
《北京市自动驾驶汽车条例》正式实施 L3级
2025-04-02 20:23





 广告
广告