基于改进的HMM方法预测驾驶员行为

摘要-先进的驾驶员辅助系统( ADAS )的开发在预测驾驶行为的研究中起着重要作用。我们开发了一种基于隐马尔可夫模型( HMM )的预测人类驾驶行为的方法。包括左/右车道变换和车道保持在内的三种不同的驾驶动作被建模为HMM的隐藏状态。基于观察(训练)，HMM方法能够使用观察到的序列来计算最可能的驾驶行为。此外，在建模过程中，观察到的序列也用于HMM的训练。为了提高模型的预测性能，我们提出了一种预滤波器将采集的信号量化为具有特定特征的观测序列。

在本论文中，将讨论并最终优化合适预过滤器的定义。这里最优性被定义为将车辆环境映射到量化状态的预滤波器的最优段。结合基于HMM的精度、检测和虚警率方面的相关结果，可以确定预滤波器的最佳参数集。利用真实人类驾驶行为的实验数据(取自驾驶模拟器)，可以得出结论，预过滤器的最佳定义可以提高检测率和准确性，同时降低误报率。驾驶行为预测的有效性已经通过与其他方法的比较得到了成功的证明

作者： 

Qi Deng, Jiao Wang and Dirk So¨ffker  

I介绍 

驾驶员辅助系统是为了帮助人类驾驶员更好、更安全驾驶而开发的系统。典型的辅助驾驶系统侧重于探测危险场景并发出警告从而避免交通事故。这类辅助系统的预测是基于诸如距离和车速等物理变量来计算的。这些物理变量描述了车辆状态和行驶环境。虽然车辆状态和驾驶环境与当前的驾驶安全评估相关，但最常见的事故原因与人类行为有关。因此，辅助驾驶系统应该帮助驾驶员检测可能的不当行为。然而，遵循一般驾驶规则，司机通常会根据自己的驾驶经验和习惯选择最合适的操作。司机的驾驶行为被认为是个人的。因此，驾驶辅助系统应该基于对个体驾驶行为的分析进行调整，以提高交通安全并实现智能驾驶。个人驾驶行为受许多因素影响，包括当前环境条件、个人驾驶特征等。因此，驾驶员的意图和下一次驾驶动作不能通过物理变量来简单而直接地测量。 

为了建立驾驶行为模型，一些方法已经被提出。例如，神经网络( NN )模型已经被用于预测[ 1 ]高速公路上车辆跟驰的加速度分布。在[ 2 ]动态贝叶斯网络( DBN )被用于估计和预测四向交叉路口的车辆跟踪和变道的加速度以及转弯率。在[ 3 ]中，通过使用特征函数来评估情境情境，预测交通参与者的下一个状态，提出了一个完全概率模型。《[ 4 ]》的作者使用了一个模糊逻辑( FL )模型，该模型是由驾驶员根据经验观察到的高速信号交叉口的行为建立的。 

在我们的研究中，使用了隐马尔科夫模型( HMM )方法预测驾驶行为，该方法用于估计不可观察状态，不可观测状态可以通过基于期望最大化( EM )和最大似然估计( MLE )的观测状态来推断，这是分别估计HMM参数和最可能隐藏状态的标准方法[ 5 ] [ 6 ]。为了改进性能建模，必须定义观察状态的适当部分。实验结果显示，使用那些合适的观察段范围，可以提高驾驶行为预测模型的质量。 

Ⅱ基于隐马尔可夫模型的驾驶行为预测 

隐马尔可夫模型（HMM）已经被成功应用于语音识别和合成[7]、生物学中的DNA轮廓识别[8]以及视频[9]中的人类行为识别等领域。如今，HMM的应用已经扩展到越来越多的研究领域，例如驾驶行为识别和预测。在[10]中，作者提出使用HMM来确定各种车辆操纵的驾驶员意图。此外，HMM通常与其他算法一起使用。在[11]中，作者提出了一种混合状态系统（HSS）-HMM框架，用于估计交叉口的驾驶员行为。驾驶员行为和车辆动力学被建模为HSS， HSS提供系统架构，HMM定义系统组件之间的关系，HMM和相关基本算法的详细定义在[5]中描述。 

HMM描述了两个随机过程之间的关系：一个由一组未观察到的(隐藏的)状态S = {S1，S2，...SN}，其中N为无法直接测量的隐藏状态的数量。另一个随机过程由一组M个可观察符号V ={V1，V2，...VM}。隐藏状态和观察符号位于，时间t分别被定义为Qt和Ot。因此，隐藏状态序列是Q= {Q1，Q2，...QT}，观察序列是O = {O1，O2，...OT}，其中T是序列的长度。使用HMM参数的序列可以通过分析观察序列来确定未观察到的状态。 

在我们的研究中，驾驶行为主要考虑车道变换。执行的驾驶操纵是隐藏状态。它们包括左/右车道变换和正常车道保持，因此N = 3.驾驶行为预测模型可视为标准HMM，如图1所示 

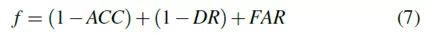
图1.具有3种状态的HMM模型 

驱动行为表示为Si，观察值Vk表示为下标k。该模型可以定义为一种系统，其中驾驶行为以状态转移概率ai j = P（Qt = S j | Qt-1 = Si），i，j [1，N]切换到另一个，这意味着从状态Si移动到状态S j的概率。所有转移概率ai j可以构成状态转移概率矩阵

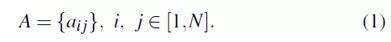
观察概率b j ( k )定义了在时间t从状态S j产生观察Vk的概率，这意味着b j ( k ) = P ( Ot = Vk | Qt = S j )。相应的观测概率分布矩阵表示为

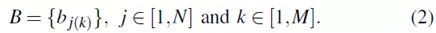
为了描述HMM，有必要使用初始概率分布，其指示在状态Si中开始的概率，其中

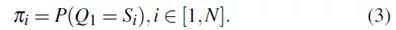
使用以上定义，完整的HMM可以定义为λ= ( A，B，π)。 

为了实现基于HMM的驾驶行为预测，该过程必须分为两部分：第一部分是模型的训练，第二部分是估计最可能的隐藏状态序列。为了训练HMM，Baum - Welch算法（也称为期望最大化）将被用来估计最大似然模型参数 λ= ( A，B，π)。在给定的观察序列O及其对应的隐藏状态序列Q中，HMM λ的参数被计算和调整以最佳地拟合这两个序列。基于保存的HMM λ，使用Viterbi算法计算具有最高概率的驾驶行为的最可能序列。 

如前所述，隐藏状态序列将由观察序列确定。因此，选择描述组成观察状态的当前状况的参数是非常重要的。这些参数必须考虑到数据收集的可行性，并具备达到模型识别目的的能力。当司机在高速公路上行驶时，ego车辆和其他周围车辆之间的关系是影响司机决策的主要因素。在我们的研究者中，与前方车辆的相对速度、ego车辆和周围车辆之间的距离被选择作为观察变量，即时间t的观察向量被定义为

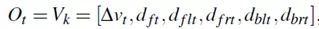
其中k∈[ 1，M ]，M是观察选择的数量。表I给出了参数的细节。在我们的研究中，驾驶模拟器用于收集每个参数的数据。在现实世界中，这些参数将取自不同的传感器，如照相机、雷达、激光雷达和超声波。[12]

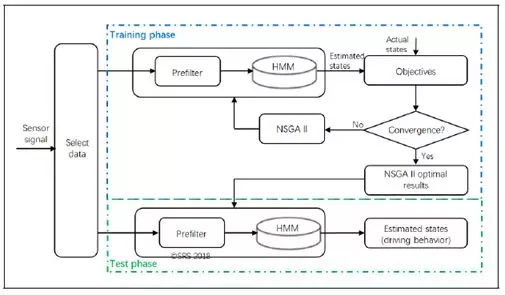
在驾驶过程中，所有观察参数都被认为是可测量的。信号是动态的，随时间变化。每个参数的改变将导致观察向量的改变。这里假设通过预滤波实现的量化信号，这在汽车领域中是典型的，使用精度有限的相关电子设备。在预滤波器的输出端，导出了以特征向量为特征的量化信号。通过使用特征向量，应该区分不同的驾驶情况。基于预滤波器，每个观测参数的信号数据将被分成多个段。每个片段代表一个相应的观察结果。因此，线段的范围很重要，将被定义来描述观察结果。使用这些分段范围，可以处理和组合信号以形成HMM预测过程的特征。为了简化建模过程，在这个贡献中定义了一个预滤波器，它只使用两个不同的范围值，并将每个观测参数分成三个部分。表I中显示了每个观测参数的左阈值和右阈值(即两个范围值)。显然，观测段范围的值非常重要，因为它们隐含地定义了HMM训练的观测序列，并最终影响了精度。 

图2.最佳预过滤器定义说明 

一个简单的方法是根据一般驾驶规则选择一个通用预过滤器，例如在德国，50m是高速公路上两个导向柱之间的相应距离。因此，距离的分段范围值可以定义为50m和100 m，速度计上的间隔可以用来表示相对速度的范围值，例如10公里/小时和20公里/小时。