广告
分子动力学在汽车空气动力学中的应用
2018-12-01 23:06:19· 来源：索辰信息
N-S方程在流体力学领域占有着举足轻重的地位，在其基础上经过数代人的理论研究，各大软件厂商对算法耕耘优化，市场上涌现出大量的N-S方程为核心的流体软件，所以
N-S方程在流体力学领域占有着举足轻重的地位，在其基础上经过数代人的理论研究，各大软件厂商对算法耕耘优化，市场上涌现出大量的N-S方程为核心的流体软件，所以在很长一段时间里，N-S方程就是CFD的代名词。然而随着工业的发展，需求在信息化以及工业化层面的深入，产能工具本身也需要理念更新效能升级。整个汽车制造业运行在更快更准更经济的道路上，期间如同新能源车开始抢占燃油车的市场那样，N-S方程阵营也面临着其他理念的挑战，竞争之下必有性能迭代，服务迭代，对我们最终用户来说，好处不言而喻。
随着生活节奏加快，汽车的行驶速度也日益提高，降低汽车的燃油消耗成为车辆设计主要任务之一。对于SUV 车型而言，为降低高速行驶时的油耗，改善车辆外型气动特性是有效的方法之一。气动特性不仅影响着整车的动力性、经济性，而且影响着车辆的操纵稳定性。在车辆上部主体造型冻结的前提下，优化车辆底部结构是降低整车风阻特性另一个研究方向。然而通过传统实验的方法来进行车辆构型设计指导，存在耗时长，代价高昂的缺点。对于初期定型时期来说，利用实验手段是无法做到对5-10个构型进行短时间集中定量测试实验的。
基于计算流体力学（CFD）的汽车空气动力学数值模拟技术现已在汽车行业广泛应用。但以往的数值计算大多基于有限体积法、有限差分等有限元方法，世界上大部分的商业软件也都是基于有限元方法。近年来，基于分子动力学的流体计算方法有了长足的进步，并已进入实际应用，美国EXA公司的PowerFlow软件近些年，常被应用在实际汽车工程项目中，与实验风洞结果相比，分子动力学方法的精度得到了很好的证明。中国索辰公司的Aries软件同样基于分子动力学技术，目前已运用在国内多个行业，如航空、船舶、地面交通等。
1. 理论基础
与大多数商业计算流体力学（CFD）产品不同，本文运用的CFD软件Aries，物理引擎是基于分子动力学理论而不是连续介质动力学方程。相比于连续介质假设，分子动力学具有的优点有：应用范围更广，精度更高，更接近实际物理现象，更直接的建模。
分子动力学方法的建模思路为：将流体分解为大量位于网格节点上的离散流体质点粒子，粒子按碰撞和迁移规则在网格上运动，通过对各网格流体质点及运动特征的统计，获得流体宏观运动规律。
Boltzmann方法（Boltzmann Method）是建立在分子运动论（即分子热输运方程组）和统计力学基础上的一种模拟流场的数值方法，其粒子分布函数满足Boltzmann方程。
Boltzmann方程是分子气体动力学的基本方程，在整个稀薄气体动力学中占据中心的地位。在自由分子流领域, 用无碰撞Boltzmann方程, 有时用它的平衡解，Maxwell分布。在滑流领域，基本方程N-S方程和Burnett方程和滑移边界条件是从解Boltzmann方程的Chapman-Enskog展开得到的, 或者要系统地对Boltzmann方程应用渐近方法得到流体力学方程。在过渡领域则要从Boltzmann方程或用与之等价的方法求解气体流动问题。
Boltzmann方程有自变量多的特点。这给数值求解带来在相空间布置宠大数目网格点的巨大困难，一般情况下解析解是不可能的, 数值求解也很困难。但多年来, 还是发展了一些方法对其求解。
矩方法是将Boltzmann方程乘以某个分子的量Q, 再将其对整个速度空间求矩（求积分）而得到矩方程。N-S方程和Burnett方程就是利用Chapman-Enskog展开求解Boltzmann方程的一阶和二阶矩方程。在过渡领域要引入新的矩和矩方程, 这方面没有唯一的可以遵循的方法。对于定常一维流动的一些个别问题, 矩方法可以得到较好的效果。
模型方程方法是鉴于Boltzmann方程右端碰撞项的复杂性而用简化的碰撞项来代替它。最著名的是BGK模型方程，BGK方程因其简单而被广泛应用。有一类有实际意义的小扰动问题, 是用BGK方程而不是Boltzmann方程求解的。现今有很多商业软件都借用了模型方程方法使Boltzmann方程数值化可编程化，其中著名的有Powerflow，Aries等。本文运用基于分子动力学流体软件Aries来进行流场分析。
2. 虚拟风洞数值模型
2.1. 汽车模型
以某款SUV为研究对象，以分析全车流场为目标，建立虚拟数值模型。
模型高度为1630mm，不带侧后视镜宽度为1910mm，车长4430mm，单侧后视镜宽度285mm，地盘离地高度为227mm，胎宽237mm，后部导流板长361mm，正投影面积为2.588m2。
除了车身车壳之外，侧后视镜、ABC柱、前脸格栅、轮胎、轮眉、车底盘构建等等车辆零部件细节都按照原设计全尺寸模型建模并导入Aries软件，不在CAD模型的基础上做模型简化前处理。
（a）SUV车底
（b）后导流板
（c）侧后视镜
图1 SUV计算模型
图2 计算流域
图3 计算背景网格划分（为方便显示加密区域，在轮胎中心登高的层面上切）
2.2.流场控制方程
1954年，Bhatnager, Gross 和Krook曾假设, 那些描述涡与涡之间相互作用的、真实的碰撞作用的具体细节并不重要, 他们提出了一个简化的碰撞模式。Aries引用BGK的简化碰撞模型概念，对Boltzmann方程做模型方程方法简化，对输运方程进行离散求解, 得到简化碰撞模型的玻尔兹曼方程：
在这种形式的玻尔兹曼方程中，碰撞表达式中包含了在特征时间尺度内达到局部平衡分布这一松弛项，它描述了分子相互作用的物理本质，为分子碰撞时间, 又可称为松弛时间。在湍流模式中, 可用一个典型的湍流松弛时间代替。该模型的演化从形式上看是一个松弛过程，通过对微观的粒子密度分布函数及其平衡态进行松弛加速, 使得系统快速地演进到符合客观规律的状态。
利用Chapman-Enskog展开，将分布函数展开为正比于数的幂次的级数：
式中，f(0)为f零级近似，f(r)为f(0)的r级修正项。而相应的应力张量Pij和热流向量qi可写作：
式中
分布函数f的一级近似f(l)解得为
将对应的应力张量和热流向量带入能量守恒方程和动量守恒方程，即得N-S方程组。
解决高雷诺数湍流流动问题，有效途径为将湍流流动模型与上述模型方程方法结合起来。Aries在Boltzmann方程中引入了大涡模式（LES），即对方程进行滤波，保留大尺度进行计算，小尺度的作用由涡黏性系数计算。
2.3. 计算结果分析
（a）风阻力时间历程曲线
（b）气动升力时间历程曲线
图 4 气动力时间收敛曲线
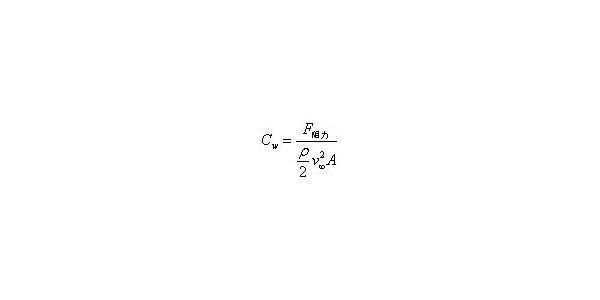
图4（a）为阻力随时间收敛曲线，取无明显波动的0.08s~0.11s时间段的数据做平均，可得SUV受到的阻力为558N，结合车辆正投影面积，得风阻系数为0.317，处于主流SUV风阻系数0.30~0.40范围区间内。
图4（b）为升力随时间收敛曲线，同样取无明显波动的0.08s~0.11s时间段的数据做平均，可得SUV受到的阻力为188N，则升力系数为0.101。
从速度流线分布和速度矢量分布可知：车后部有较大流动分离区。车顶后缘的导流板，超出车身的延伸段向后向下构型，气流经导流板后继续向下运动，并发生分离；车尾部下方的上翘构型，使得从车底流经气流方向向上偏移。车后的分离区域，由于构型优化而减小，然而尾流区仍然延伸到了车后约三分之一个车位的距离；车顶导流板有效地使上部分离区域控制在后窗的范围，后窗的斜向后倾斜设计也限制了涡流向下运动，进而减小了涡流大小，在后床上的这片低速区，是长时间行驶后，后窗积灰程度明显高于前窗的主要原因；车底轮胎区域出现了流线分布，有涡流区，也是车行风阻的一部分。
图 5 横向流线分布(车头局部)
横向流线检视区域设在轮眉水平高度。车前侧面到前轮轮眉部分，流线大致呈向上绕流，过轮眉后向下流动，由于上方有侧后视镜，所以流线将通过轮眉及后视镜之间较狭窄的区域，流速有一个明显升高，推测将加剧后视镜后的涡流脉动，使得行驶噪声加大，后续应对此处做具体声场分析，关注噪声成因。
横向流线分布更为清晰地显示了车尾部的大涡流区域；车底盘件虽然没有进行有效包附，然而车底流线分布却并未出现大面积紊乱以及涡流，仅在后轮后方有明显的流动分离区域；气流流过车底后，经车底扩散向后排出，与车辆侧面绕行过来的气流在车后形成的涡流相结合，造成向车辆行驶方向相反行进的下洗流。
图 6 车底横向流线分布(车尾局部)
3. 结论
Aries软件基于分子动力学原理，可对车辆等内部构型复杂精密的器械结构，做全时域流场分析，定制化的虚拟数值风洞模块可对现实实验环境做到全建模，且支持全细节模型直接导入仿真，使设计人员在设计车辆细节时，如后视镜，车顶后缘导流板，车底盘包附构建等，可与车辆整体一起做模拟，全面分析该细节对整车设计的影响。
经研究，某SUV，风阻系数为0.317，处于主流SUV风阻系数范围之内，车辆细节分析符合设计初衷：
1. 车顶导流板起到减小分离区域的作用；
2. 车底盘布局，使流线分布整齐，没有大的分离区域，并未大幅度增加风阻；
3. 轮胎仍需增加挡风板来阻断气流穿过形成涡流，而增大风阻。
由于基于高阶的控制方程，玻璃表面的声压结果得以保存下来，结果无需通过声类比方法进行声源模拟，便可以直接进行声场分析。
参考文献：
[1] 谷正气. 汽车空气动力学[M]. 人民交通出版社, 2005
[2] 沈俊, 傅立敏, 黎妹红等. CFD软件及其在汽车领域的应用[J]. 汽车研究与开发, 2000,(5):40-43
[3] 沈俊, 傅立敏, 范士杰，CFD在汽车空气动力学设计中的应用[J]. 汽车技术, 2000 ,(10):1-4
[4] 于萍. 工程流体力学[M].科学出版社.
[5] HARRIS, STEWART. An introduction to the theory ofthe Boltzmann equation[M]. Dover Books, 1971.
[6] WALTER G. VINCENI. Introduction to Physical gasdynamics[M]. Krieger Publishing, 1965.
[7] 沈青. 稀薄气体动力学[M]. 国防工业出版社.
[8] 张克鹏. 基于PowerFlow的某重型牵引车外流场数值分析[J], 汽车工程师, 2013, (5):25-28
[9] 潘小卫, 谷正气, 何忆斌等, F1赛车气动特性的CFD仿真和试验研究[J], 汽车工程, 2009, 31(3):274-277
[10] 李明, 沈伋等, 格子-玻尔兹曼方法在舰面流畅计算中的应用[J], 飞机设计, 2017, 37(2):11-14
广告 
广告
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
广告
广告
